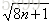441. Arranging Coins(可用二分搜索)
题目地址:https://leetcode.com/problems/arranging-coins/description/
You have a total of n coins that you want to form in a staircase shape, where every k-th row must have exactly k coins.
Given n, find the total number of full staircase rows that can be formed.
n is a non-negative integer and fits within the range of a 32-bit signed integer.
Example 1:
n = 5 The coins can form the following rows: ¤ ¤ ¤ ¤ ¤ Because the 3rd row is incomplete, we return 2.
Example 2:
n = 8 The coins can form the following rows: ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Because the 4th row is incomplete, we return 3.
// 两种方法
方法一:
class Solution {
public int arrangeCoins(int n) {
long lo = 1, hi = n; // lo和hi定义为long纯属为了方便mid赋值,int范围够了
long mid;
if (n == 0) return 0;
while (hi - lo > 1) {
mid = (lo + hi) >>> 1; // 这里mid要定义long,虽然这里不会因为加法溢出而导致mid出问题,但是下面的mid*(1+mid)>>>1这个表达式默认int,可能出现乘法溢出,远远超出int范围,二进制多出的高位部分已经被截断了,会导致结果错误。
long sum = mid * (1 + mid) >>> 1; // sum一定要long因为int取值到2147483647有一步会得到的1297036691877396480
if (sum > n) {
hi = mid;
} else {
lo = mid;
}
}
return (int)lo;
}
}如果觉得mid=(lo+hi)>>>1不好理解,那就换成mid=lo + ((hi - lo) >>1)吧,因为lo在int范围,hi在int范围,hi-lo也在int范围,而lo+(hi-lo)>>1是小于hi的,所以也是int范围。关于为什么>>>1更好可以看我的另一篇博客:https://blog.csdn.net/qq_34115899/article/details/79859973
但是>>>1只能解决加法溢出的问题,几乎是解决不了乘法溢出的问题(除非有类似乘以2再>>>1的巧合,高位数据是被截断的,没有保存),解决办法是选用更大的数据类型来处理乘法溢出问题。
方法二:
很容易想到直接用数学方法
X*(1+X)/2≤n
X+X2 ≤ 2n
这里就要用配方法
4X+ 4X2 ≤ 4*2*n
(2X+1)2 - 1 ≤ 8n
2X+1 ≤
X ≤
写成代码:
class Solution {
public int arrangeCoins(int n) {
double t = 8.0 * n + 1; // 不能写成8*n+1,这个表达式是默认int,可能超出int范围导致结果错误,所以换成8.0,表达式就成为double型
return (int)((Math.sqrt(t) - 1) / 2);
}
}========================================Talk is cheap, show me the code=======================================