二叉树之红黑树
红黑树
概述
红黑树是一种自平衡的二叉查找树。是计算机科学中用到的一种数据结构。
1972年出现，当时被称之为平衡二叉B数。后来，1978年被修改为如今的红黑树。
它是一种特殊的二叉查找树。红黑树的每一个节点上都有存储位表示节点的颜色。每一个节点可以是红色或者黑色。
红黑树不是高度平衡的，它的平衡是通过红黑规则进行实现的。
为什么要有红黑树？？？
在此之前，我们学习的是平衡二叉树，其高度平衡，左右子树不超过1。这样子可以使查找效率控制在 O(logn)，但是这样子也照成了不变！每当出现了不平衡的情况都要进行“左旋”，“右旋”处理，有点过于繁琐，故红黑树中做出了改进，只遵循自己的红黑规则！
特点
-
平衡二叉B树
-
每一个节点可以是红或者黑
-
红黑树不是高度平衡的,它的平衡是通过"自己的红黑规则"进行实现的
红黑规则
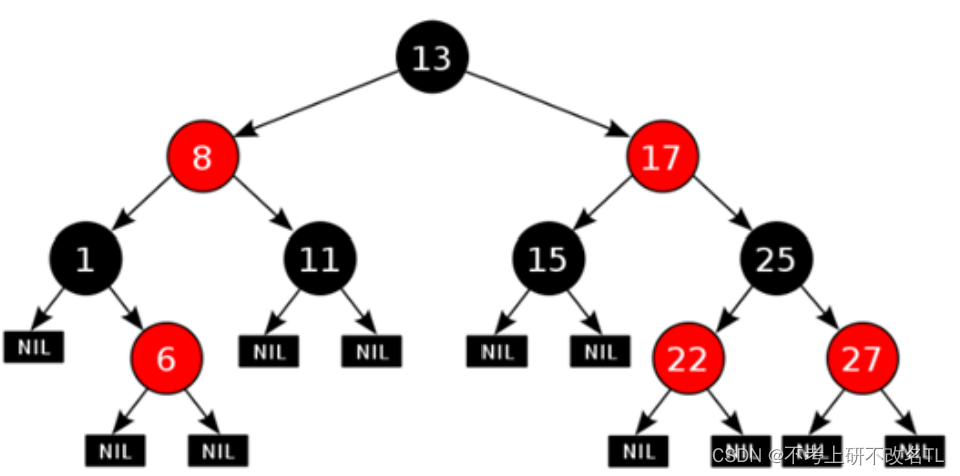
我们可以参照图片进行讲解
（1）每一个节点或是红色的，或者是黑色的。
（2）根节点必须是黑色。
（3）如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为Nil，这些Nil视为叶节点，每个叶节点(Nil)是黑色的。
上述图中，结点1，6，11，15，22，27它们都没有子节点，所以它们的左右指针都是NIL(空)，且NIL的颜色都必须是黑色的；
节点13是根节点，所以它没有父节点，它的父节点的地址为空，即标记为NIL。
（4）如果某一个节点是红色，那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)。
（5）对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。
例如节点 8 来说，它到其所有后代叶节点的简单路径的黑色节点个数都是2。
8->1->NIL ，8->1->6->NIL ，8->11-NIL路径上的黑色节点都是2个。
如何在红黑树上添加节点？
添加节点的颜色可以是红色，也可以是黑色。
（1）我们不妨假设加入的节点都是黑色
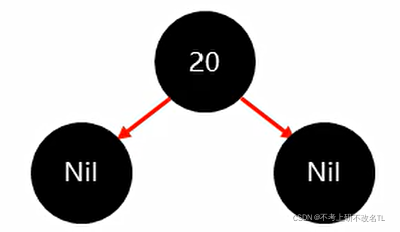
序列为20 ，18 ，23；过程如下：
先是20，将其设为根节点
再插入18，此时违背了红黑规则，（即违背了第5条红黑规则）
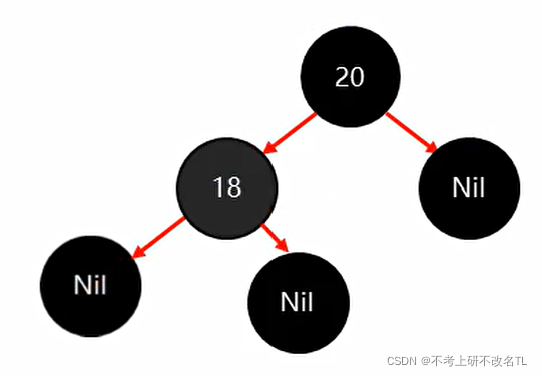
所以我要将18改为红色即可
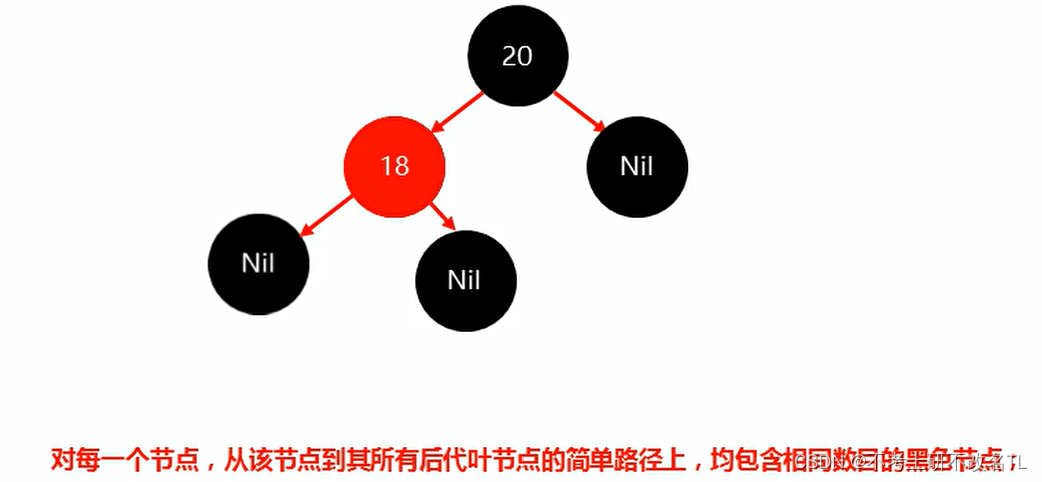
最后将23插入，同样这样子也违背了红黑规则，处理方法与上面类似
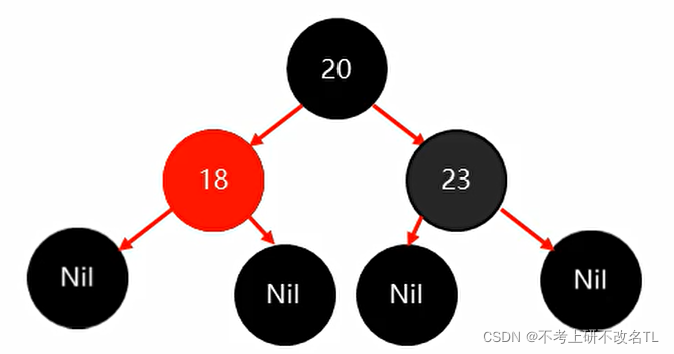
将23节点改为红色即可
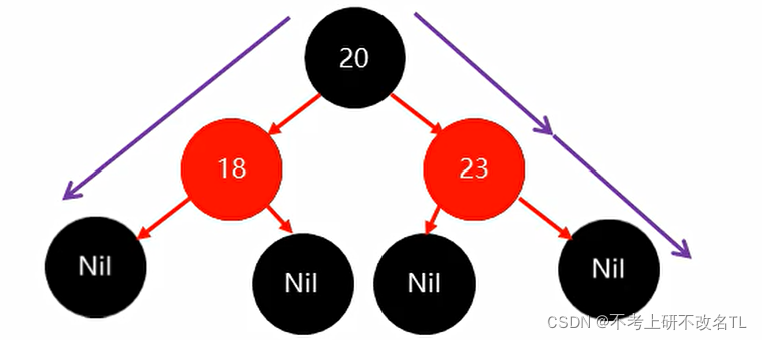
故添加3个元素，一共需要调整2次。
（2）如果我们加入的节点都是红色
序列为20 ，18 ，23；过程如下：
一开始我们将红色的20节点插入，显然此时已经违背了红黑规则，（根节点必须为黑色）
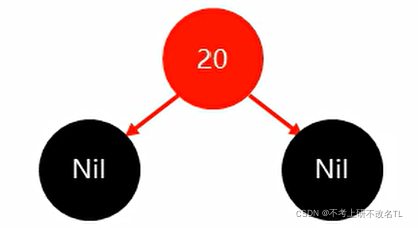
所以需要将20改为黑色，结构如下：
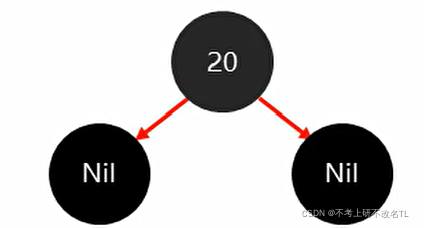
再将18插入，此时满足红黑规则，不需要调整
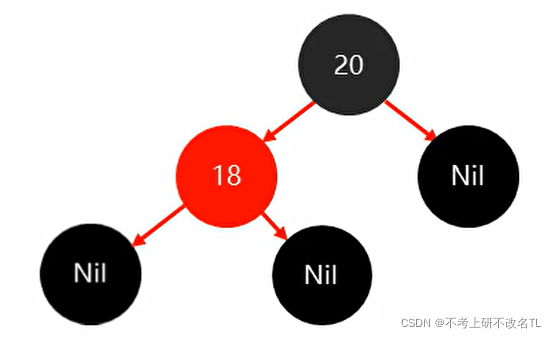
最后插入23，也没有破坏红黑规则，故无需调整
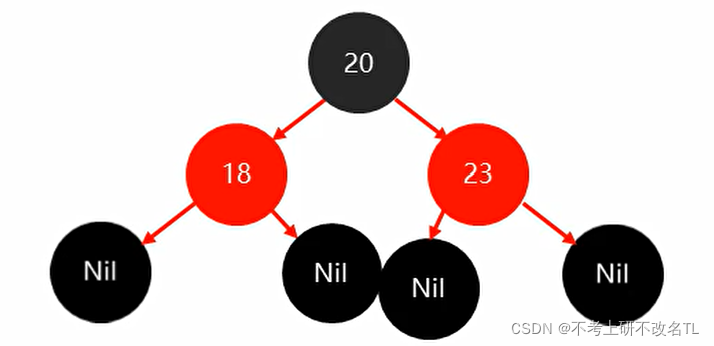
所以，如果添加的3个节点为红色，只需要调整1次即可！
所以添加元素的时候尽量选择红色，这样子效率高！！！
红黑树添加节点后如何保持红黑规则
之后我们在添加节点的时候，都默认是红色的节点，因为这样子效率高！
从左到右一次插入节点，构建红黑树。
先将20插入，由于其为第一个节点，即根节点，所以将其改为黑色。
然后依次插入18，23，由于满足红黑规则，所以不要做任何操作
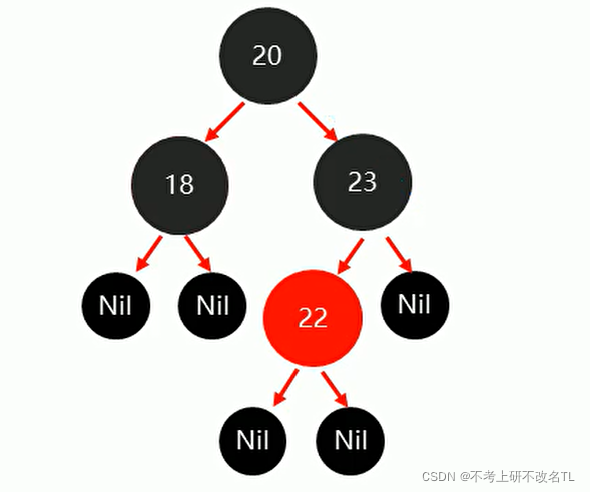
插入22时，稍微有一点复杂！如下图所示：
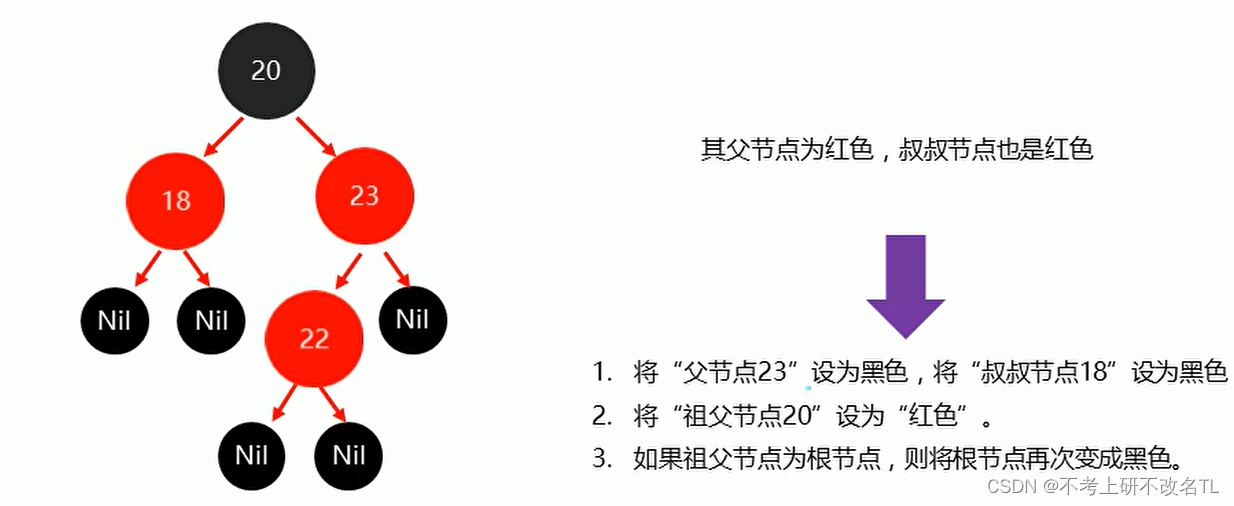
按照上述图片进行修改后，树状结构如下所示：
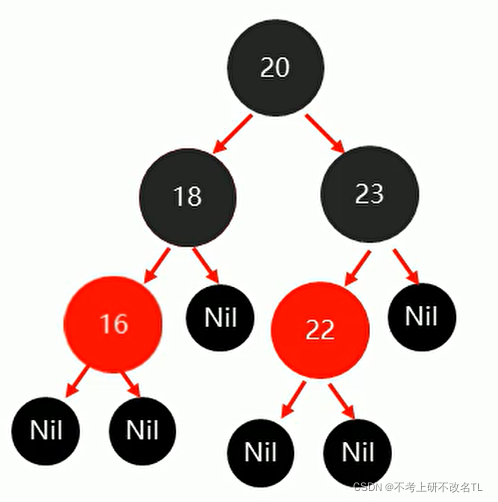
继续添加16节点
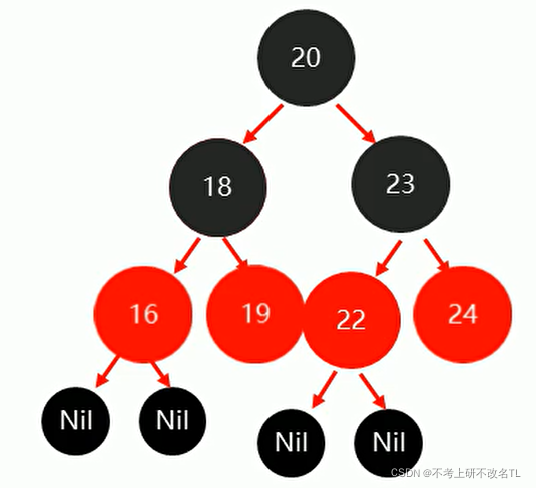
再者添加24，19两个节点都不用进行任何操作！最终结果如下图所示：
添加规则综述
-
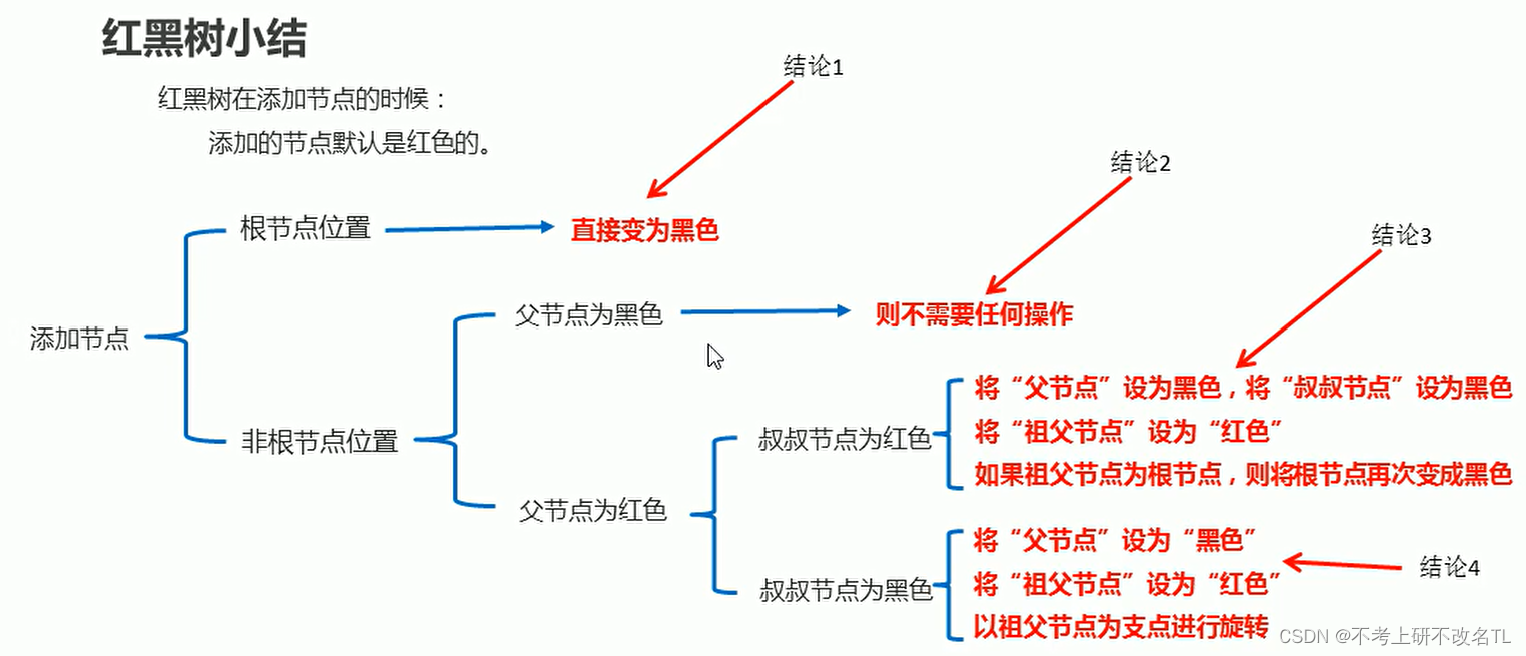
根节点位置
-
直接变为黑色
-
-
非根节点位置
-
父节点为黑色
-
不需要任何操作,默认红色即可
-
-
父节点为红色
-
叔叔节点为红色
-
将"父节点"设为黑色,将"叔叔节点"设为黑色
-
将"祖父节点"设为红色
-
如果"祖父节点"为根节点,则将根节点再次变成黑色
-
-
叔叔节点为黑色（复杂！）
-
将"父节点"设为黑色
-
将"祖父节点"设为红色
-
以"祖父节点"为支点进行旋转
-
-
-
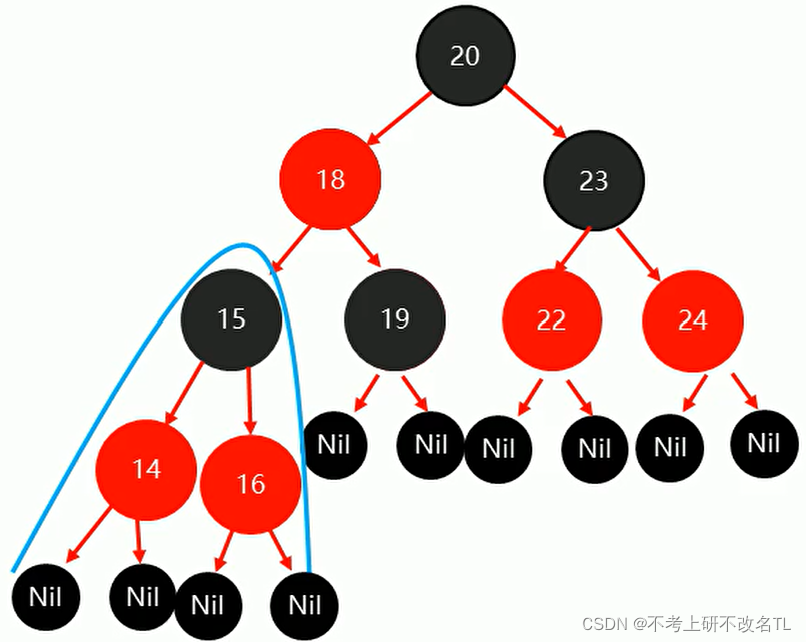
这里分析一下当父节点是红色，叔叔节点为黑色时的具体操作，同样以上述例子：
此时要插入14节点
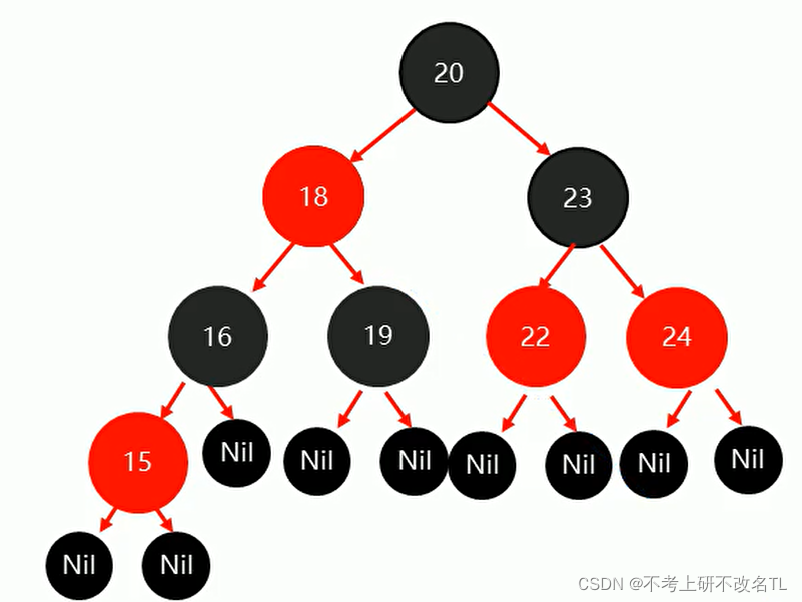
插入后结果如下
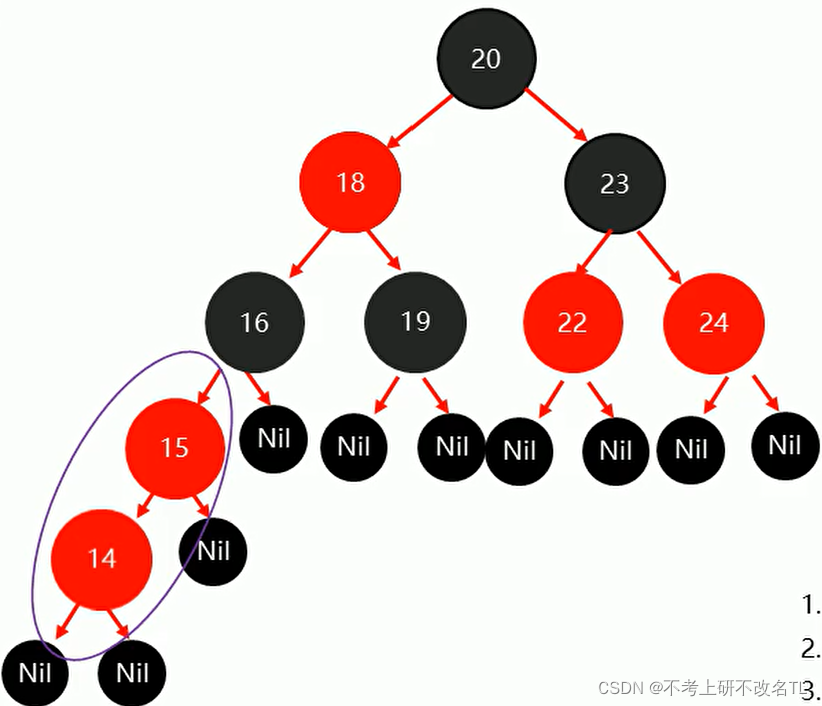
（1）先将父节点15，设置为黑色
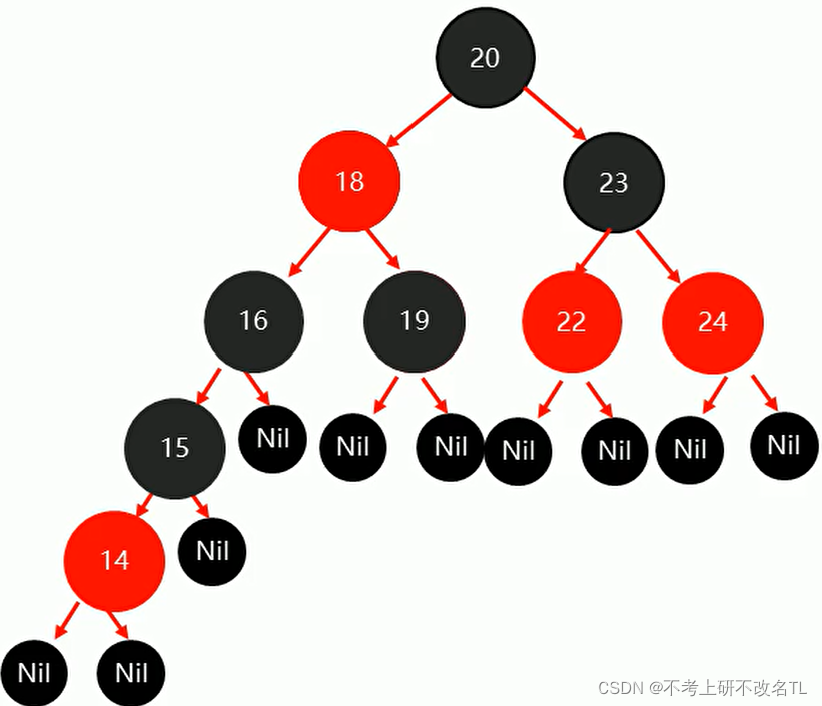
（2）再将祖父节点16，设置为红色
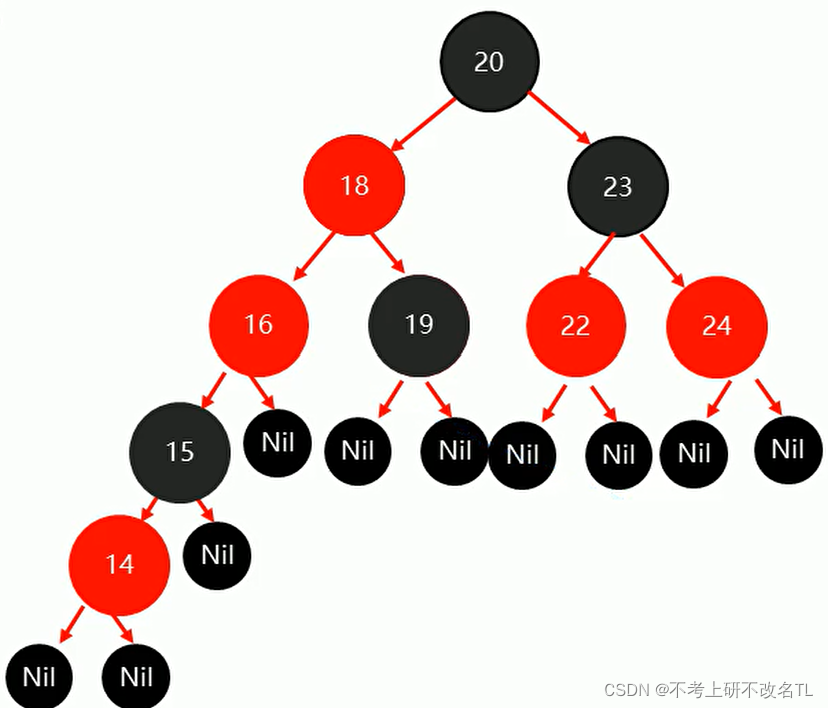
（3）最后以祖父节点为支点进行旋转
