[bzoj2125]最短路

传送门

仙人掌最短路，圆方树！
先dfs找环，顺带求出环的长度len，记录每个点到环内深度最小的点的最短路径有没有经过返祖边
对于每个环建一个方点，都是圆方树的基本操作啦！
求答案时对于\(dist(x,y)\)，先求出\(z=lca(x,y)\)，然后判断\(z\)是否是方点
1、z是方点，那么x和y的最短路径经过了一个环，那么我们对于x和y就少跳一步，跳到z的儿子处。
对应的圆方树是这样的：

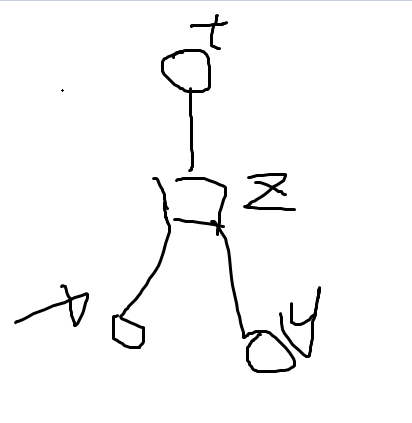
原图上是这样的：

很显然这个时候需要分类讨论了：（x，y是跳了后的x，y）
假如x和y的最短路径都经过返祖边或者都不经过返祖边，并且不知道t-x和t-y哪条是返祖边的情况下，最短距离就是\(min(abs(dep[x]-dep[y]),min(len-dep[x]+dep[y],len-dep[y]+dep[x]))\)
否则就是只有一条经过返祖边，答案就是\(min(len-(dep[x]-dep[z])-(dep[y]-dep[z]),(dep[x]-dep[z])+(dep[y]-dep[z]))\)

2、z不是方点，那么直接算就是了，答案就是\(dep[x]+dep[y]-2*dep[z]\)（x，y是读入的x，y）

代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
void read(int &x) {
	char ch; bool ok;
	for(ok=0,ch=getchar(); !isdigit(ch); ch=getchar()) if(ch=='-') ok=1;
	for(x=0; isdigit(ch); x=x*10+ch-'0',ch=getchar()); if(ok) x=-x;
}
#define rg register
const int maxn=2e4+1e3;
int n,m,q,dep[maxn],top,id,f[maxn][21],dis[maxn],len[maxn],ans;bool vis[maxn*2],w[maxn*2];
struct o{int x,id;}st[maxn];
struct oo{
	int pre[maxn*2],nxt[maxn*2],h[maxn*2],v[maxn*2],cnt;
	oo(){cnt=1;}
	inline void add(int x,int y,int z)
	{
		pre[++cnt]=y,nxt[cnt]=h[x],h[x]=cnt,v[cnt]=z;
		pre[++cnt]=x,nxt[cnt]=h[y],h[y]=cnt,v[cnt]=z;
	}
}a,b;
void dfs(int x,int fa)
{
	for(rg int i=a.h[x];i;i=a.nxt[i])
		if(a.pre[i]!=fa)
		{
			if(!dep[a.pre[i]])st[++top].x=x,st[top].id=i,dep[a.pre[i]]=dep[x]+a.v[i],dfs(a.pre[i],x),top--;
			else if(dep[a.pre[i]]<dep[x])
			{
				++id,b.add(id,x,min(dep[x]-dep[a.pre[i]],a.v[i]));
				int g=min(dep[x]-dep[a.pre[i]],a.v[i]);len[id-n]+=a.v[i];
				if(g==a.v[i])w[x]=1;vis[i]=vis[i^1]=1;int ttt=top;
				while(a.pre[i]!=st[top].x)
				{
					int t=st[top].x,g=min(dep[t]-dep[a.pre[i]],dep[x]-dep[t]+a.v[i]);vis[st[top].id]=vis[st[top].id^1]=1;
					if(g==dep[x]-dep[t]+a.v[i])w[t]=1;b.add(id,t,g),len[id-n]+=a.v[st[top].id],top--;
				}
				int t=st[top].x;b.add(id,t,0);len[id-n]+=a.v[st[top].id];
				vis[st[top].id]=vis[st[top].id^1]=1;top=ttt;
			}
		}
}
void dfs1(int x,int fa)
{
	for(rg int i=1;i<=20;i++)
	{
		if(dis[x]<(1<<i))break;
		f[x][i]=f[f[x][i-1]][i-1];
	}
	for(rg int i=b.h[x];i;i=b.nxt[i])
		if(b.pre[i]!=fa)f[b.pre[i]][0]=x,dis[b.pre[i]]=dis[x]+1,dep[b.pre[i]]=dep[x]+b.v[i],dfs1(b.pre[i],x);
}
int lca(int x,int y)
{
	if(dis[x]>dis[y])swap(x,y);
	int poor=dis[y]-dis[x];
	for(rg int i=20;i>=0;i--)if(poor&(1<<i))y=f[y][i];
	for(rg int i=20;i>=0;i--)if(f[y][i]!=f[x][i])x=f[x][i],y=f[y][i];
	return x==y?x:f[x][0];
}
int jump(int x,int z)
{
	int poor=dis[x]-dis[z]-1;
	for(rg int i=20;i>=0;i--)if(poor&(1<<i))x=f[x][i];
	return x;
}
int main()
{
	read(n),read(m),read(q);id=n;
	for(rg int i=1,x,y,z;i<=m;i++)read(x),read(y),read(z),a.add(x,y,z);
	dep[1]=1,dfs(1,0);for(int i=2;i<=a.cnt;i+=2)if(!vis[i])b.add(a.pre[i],a.pre[i^1],a.v[i]);
	memset(dep,0,sizeof dep),dfs1(1,0);
	for(rg int i=1,x,y,z,l,r;i<=q;i++)
	{
		read(x),read(y);z=lca(x,y);ans=0;
		if(z>n)
		{
			l=jump(x,z),r=jump(y,z);
			ans=dep[x]-dep[l]+dep[y]-dep[r];
			if((w[l]&&w[r])||(!w[l]&&!w[r]))ans+=min(abs(dep[l]-dep[r]),min(len[z-n]-dep[l]+dep[r],len[z-n]-dep[r]+dep[l]));
			else ans+=min(len[z-n]-(dep[l]-dep[z])-(dep[r]-dep[z]),(dep[l]-dep[z])+(dep[r]-dep[z]));
		}
		else ans=dep[x]+dep[y]-dep[z]*2;
		printf("%d\n",ans);
	}
}