二维偏序（逆序对，有序对）

---

求逆序对问题：

即例可以在数组{1，9，11，2，5，32，12}求有多少逆序对或者有序对。

我们可以转化为二维坐标系。

以数组的下标作为坐标的x轴，以数值作为坐标的y轴。

如下图

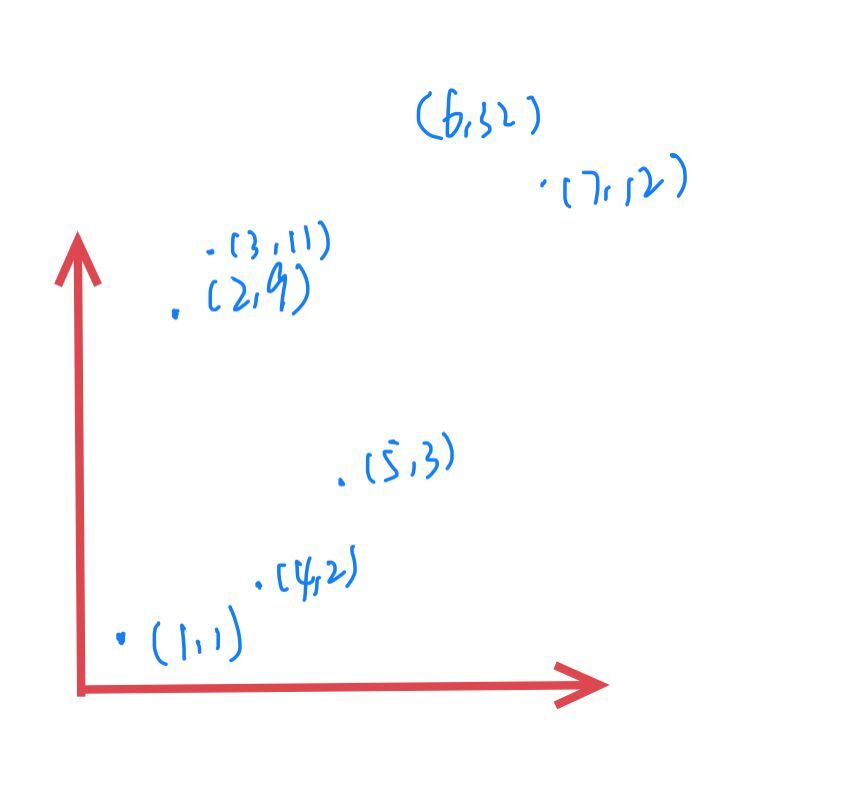
先按x轴排序，我们需要求在此点的左下方有多少点，即若现在为第k个点（xk,yk)那么求（1，k-1）之间有多少点x,y同时小于xk,yk，（此处我们求有序对），那么因为我们先按x轴排序了，所以我们只要求y轴比它小有几个就好了，这里我们用树状数组，从左到右遍历，每次求（1，yk-1）之间有几个数，然后对于（yk,max(y最大)）进行区间加1更新就可以求出来了。

顺序对代码

 

#include<bits/stdc++.h> 
using namespace std;
const int MAXN=1000010;
int maxValue,tr[MAXN];
int lowbit(int x){
    return x&-x;
}
void add(int x,int k){
    for(int i=x;i<=maxValue;i+=lowbit(i)){
        tr[i]+=k;
    }
}
int sum(int l,int r){
    int ans=0;
    for(int i=r;i>0;i-=lowbit(i)){
        ans+=tr[i];
    }
    for(int i=l-1;i>0;i-=lowbit(i)){
        ans-=tr[i];
    }
    return ans;
}
struct Point{
    int a,b;
    bool operator <(const Point &another)const{
        return another.a<a;
    }//对于x轴方向上单调递增 
};
int pointCnt=0;
int main(){
    int n;
    scanf("%d%d",&n,&maxValue);
    priority_queue<Point> q;
    for(int i=1;i<=n;i++){
        int tmpA,tmpB;
        scanf("%d%d",&tmpA,&tmpB);
        Point tmp=Point{tmpA,tmpB};
        q.push(tmp);
    }
    while(!q.empty()){
        Point nowPoint=q.top();q.pop();
        int nowValue=nowPoint.b;
        //cout<<nowValue<<endl; 
        cout<<sum(1,nowValue)<<endl;
        add(nowValue,1);//对于y轴大于nowvalue的加1 
    }
    return 0;
}

 

---