P2016 战略游戏

传送门

思路：

---

 

前置知识——普通树D：

▲普通的树形 DP ：

　　设 f [ i ][ 0 ] 表示这个点不取，则它的所有子节点都要取；f [ i ][ 1 ] 表示这个点取，则它的子节点取与不取对之前的答案没有影响，只要取两个中最优的情况。

▲转移方程式：

　　　

 

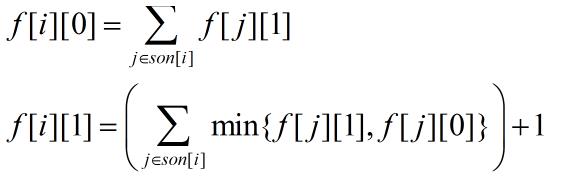
▲操作实现：

　　常采用叶→根的转移形式，根据父节点的状态确定子节点的状态，若子节点有多个，则需要一一枚举，将子节点（子树）的 DP 值合并。

---

本题思路：

　　一道 树形DP 的模板题。……答案 ans = min( f[ root ][ 1 ]，f[ root ][ 0 ] )。

标程：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<vector>
#include<stack>
#include<deque>
#include<queue>
#include<map>
#include<set>
using namespace std;
#define maxn 1501
#define min(a,b) ((a)<(b)?(a):(b))
typedef long long LL;
LL f[maxn][2],n,root;
bool bo[maxn];
struct hh
{
    LL num,son[maxn];
}t[maxn];
inline LL read()
{
    LL kr=1,xs=0;char ls;
    ls=getchar();
    while(!isdigit(ls))
    {
        if(!(ls^45))
            kr=-1;
        ls=getchar();
    }
    while(isdigit(ls))
    {
        xs=(xs<<1)+(xs<<3)+(ls^48);
        ls=getchar();
    }
    return xs*kr;
}
inline void dp(LL x)//计算以x为根的子树的值 
{
    f[x][0]=0;f[x][1]=1;//f[x][0]为节点x上不设士兵的初值，f[x][1]为节点x上设士兵的初值 
    if(!t[x].num) return;//到达叶子节点，返回
    for(LL i=1;i<=t[x].num;i++)//枚举x的每个子节点 
    {
        dp(t[x].son[i]);//递归计算第i个子节点的两个值 
        f[x][0]+=f[t[x].son[i]][1];//节点x上不设士兵，将其值累加给自己 
        f[x][1]+=min(f[t[x].son[i]][0],f[t[x].son[i]][1]);//节点x上设士兵，子节点可设可不设，选最小的累加给自己 
    }
}
int main()
{
    n=read();
    LL x,y;
    for(LL i=1;i<=n;i++)
    {
        x=read();t[x].num=read();
        for(LL j=1;j<=t[x].num;j++)
        {
            y=read();t[x].son[j]=y;bo[y]=true;
        }
    }//浅显易懂 
    root=0;
    while(bo[root]) root++;//找根节点编号 
    dp(root);
    printf("%lld\n",min(f[root][0],f[root][1])); 
return 0;
}