qbzt周末刷题班5题解

T1

读入一个\(n\),对于一个三元组\((i,j,k)\)满足要求当且仅当\(1≤i,j,k≤n\)且\(i×j≥k\)。求符合条件的三元组的数量。
对于30%的数据\(n≤100\)
对于60%的数据\(n≤5000\)
对于100%的数据\(n≤100000\)

暴力：\(O(n^3)\)暴力枚举

60pts:
\( \because i\times j\geqslant k\\ \therefore i\geqslant \lceil\frac{k}{j}\rceil \)
对于每个\((j,k)\),都有\(i\in [\lceil\frac{k}{j}\rceil,n]\)符合条件
所以我们可以枚举\(j,k\),复杂度\(O(n^2)\)

100pts(\(O(n)做法)\):
在60pts枚举时，注意到如果\(k\leqslant j\),则当前的\((j,k)\)的贡献为\(n\)。
所以将\((j,k)\)产生的贡献分为两部分：
1.\(k\leqslant j:\) 一个\(k\)的贡献为\(n\)。且对于每个\(j\),都有\(j\)个符合条件的\(k\),所以总贡献为\(j\times n\)
2.\(k>j:\) 某个\(k\)产生的贡献为\(n-\lceil\frac{k}{j}\rceil+1\)。
且当\(\lceil\frac{k}{j}\rceil=2\)时，\(k\in [j+1,2j];\)\(\lceil\frac{k}{j}\rceil=3\)时，\(k\in [2j+1,3j]........\)
最后一段：当\(\lceil\frac{k}{j}\rceil=x+1\)时，\(k\in[xj+1,n]\)\((x=\lfloor\frac{n}{j}\rfloor)\)
发现非最后一段的区间长为\(j\)，那么非最后一段的所有贡献可以加和，即\(j\times \sum_{l=2}^x{n-l+1}\),发现是一个等差数列
最后一段的贡献：\(((n-x)\times (n-xj)\)
整理一下：
\(ans=\sum_{i=1}^n i\times (n+\frac{(2n-x)(x-1)}{2})+(n-xi)(n-x),x=\lfloor\frac{n}{i}\rfloor\)
可以\(O(n)\)求出答案
PS:十年OI一场空，不开longlong见祖宗
\(Code\)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<map>
#include<cstring>
#include<cstdlib>
#include<set>
#define pa pair<int,int>
#define pi pair<ull,ll>
using namespace std;
const int inf=2147483640;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
	char ch=getchar();
	ll x=0;bool f=0;
	while(ch<'0'||ch>'9'){
		if(ch=='-') f=1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=(x<<3)+(x<<1)+(ch^48);
		ch=getchar();
	}
	return f?-x:x;
}
int n;
ull ans;
int main(){
	n=read();
	for(int i=1;i<=n;i++){
		ans+=(ull)n*i;
		ull x=n/i; 
		ans+=(ull)i*((ull)(2*n-x)*(ull)(x-1)/2);
		ans+=(ull)(n-x*i)*(ull)(n-x);
	}
	printf("%llu\n",ans);
}

T2

一些废话：连暴力都不会了.orz

先从暴力看起。我们可以枚举每一个关键点作为出发点。\(f[i][j][o]\)表示从点\(i\)到点\(j\)是否有长度\(mod\ p=o\)的路径。这样有40pts。

优化一下：如果走某条边奇数次，和走这条边一次所到达的点是一样的。走这条边偶数次，和不走所到达的边是一样的。而题目保证\(p\)是奇数。所以我们可以考虑走某条边\(p\)或\(2p\)次来调节这条边的贡献。

上面的暴力需要枚举所有关键点作为出发点，这很不优秀，我们想把它优化掉。那么我们能不能减少枚举的点的个数？

我们考虑某一点\(o\)和合法路径的关系。如果图中存在一条从\(x\)到\(y\)的合法路径，且路径上的某一点\(z\)可以到达\(o\)。那么我们可以通过走\(2p\)边\((o,z)\)来抵消这条边在模意义下的贡献。这样就可以使这条合法路径经过点\(o\)。而整个图是无向图，所有点都是联通的，所以点\(o\)可以是任意一点。这样就可以优化掉枚举起点。

优化两下：我们发现不只是边\((o,z)\)可以被调节，图上所有的边都可以被调节。那最后的路径长度只和每条边被经过的次数有关，和经过的点没什么关系。
设某条边的边长为\(A\),那么\((k_1\times A)\ mod\ p\)可以表示所有的\((k_2\times gcd(A,p))\ mod\ p\)

证明(以下简称\(gcd(A,p)\)为\(gcd\)):

\[x 设A=mp+a,a=y\cdot gcd\\ \therefore \left\{\begin{aligned}A\equiv y\cdot gcd\ (mod\ p)\\ \frac{A}{gcd}\equiv m\frac{p}{gcd}+y\ (mod\ p)\\ \end{aligned}\right.\\​ 现在我们要用k_1\cdot y\cdot gcd\ (mod\ p)来表示k_2\cdot (m\frac{p}{gcd}+y)\ (mod\ p)\\ k_2\cdot (m\frac{p}{gcd}+y)\equiv k_2\cdot m\cdot p\cdot gcd^{-1}+k_2\cdot y\ (mod\ p)\\ 即k_2\cdot (m\frac{p}{gcd}+y)\equiv k_2\cdot y\ (mod\ p)\\ 所以我们现在要用k_1\cdot y\cdot gcd\ (mod\ p)来表示k_2\cdot y\ (mod\ p)\\即用k_1\cdot gcd\ (mod\ p)来表示k_2\ (mod\ p)\\ 若k_1\cdot gcd\equiv k_2\ (mod\ p)\\则k_1\equiv k_2\cdot gcd^{-1}\ (mod\ p)\\对于任意的k_2,k_1都有解，证毕 \]

所以若存在一条路径长\(A\)使得\(gcd(A,p) | gcd(L,p)\),则存在一个\(k_1\cdot A\equiv k_2\cdot L\ (mod\ p)\)，即路径合法。\(k_1,k_2\)的问题可以通过多次走\(A\)来解决。
所以我们只需要求出所有边权的\(gcd\),看是否能整除\(gcd(L,p)\)即可

T3

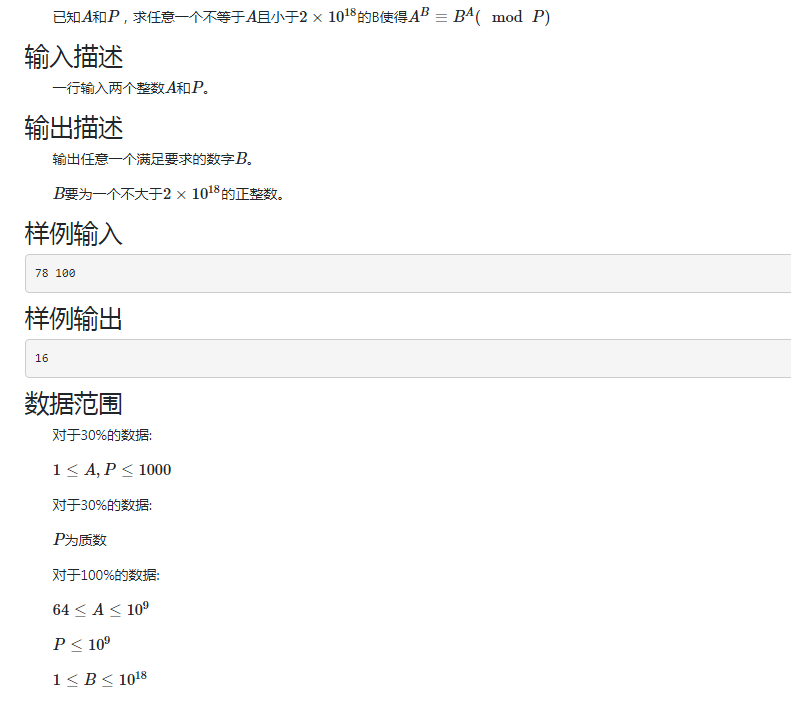
暴力：枚举\(b\),看起来有30pts，其实它有50pts

正解：
我们知道\(a^b \equiv a^{b\ mod\ p}\ mod\ p,a^a \equiv a^a\ mod\ p\),所以不妨让\(b\)与\(a\)同余,设\(b=kp+a\)。
根据扩展欧拉定理,当\(p\)与\(a\)互质时，\(a^b \equiv a^{b\ mod\ \phi(p)}\ mod\ p\)（扩展欧拉定理见这里(\(stO\)一扶苏一\(Orz\)））,设\(b=k_2\codt \phi(p)+a\)。
可得\(b=p\cdot \phi(p)+a\)
当\(p\)与\(a\)不互质时：因为\(a\geqslant 64\),所以等价于互质的情况

T4

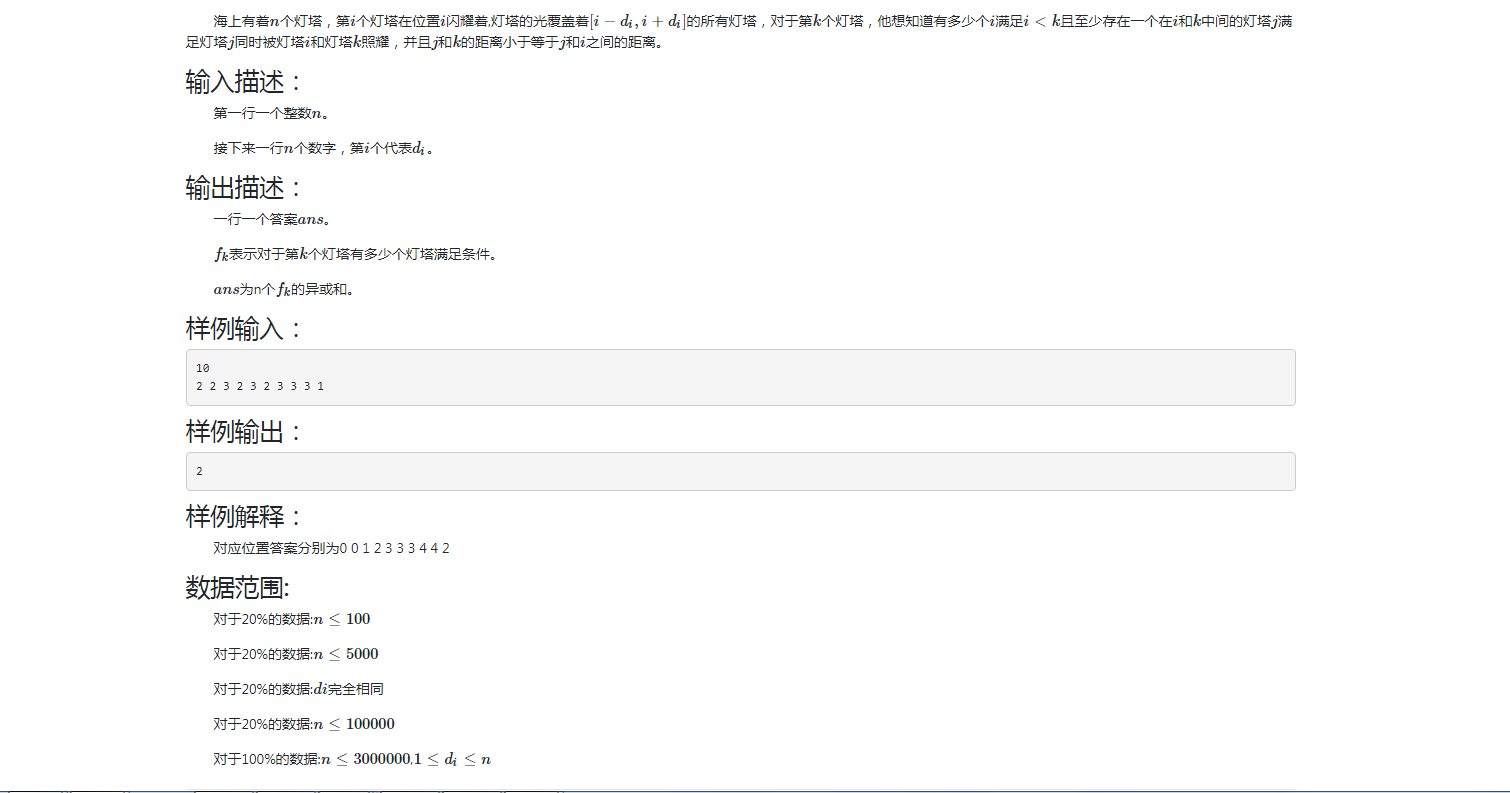
题目背景过酸已隐藏

暴力：\(O(n^3)\)暴力枚举

优化：
合法的情况：

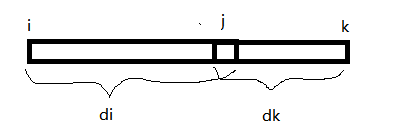
对于一个\(i\)来说，最优的\(j\)为\(i+d_i\),且\(k\)要满足\(k\leqslant 2j-i\)。因为当\(j\)为\(i,k\)中点时，\(k=2j-i\),但\(j\)更靠近\(k\)。

对于每个\(i\),可以确定一个最优的\(j\),进而确定最远可能覆盖到的\(k=2j-i\)。发现对于这时的\(i,j\)，符合条件的\(k\)的范围为\([i+2,2j-i]\)。（就算\(j>k\)也木有关系（虽然题目要求\(j\)在\(i,k\)中间）（我也不造为啥））
这样我们把\(i\)对\(f_k\)产生的贡献放到以\(j\)为下标的数组里，维护后缀和。
std:

#include<bits/stdc++.h>
#define N 3200000
#define lowbit(x) ((x)&-(x))
using namespace std;
int n,d[N],f[N];
int ans;
vector<int>a[N];
int t[N]; 
namespace bit{
	int t[N];
	int insert(int x,int a){
		x=n-x+1;
		for(int i=x;i<=n;i+=lowbit(i))t[i]+=a;
		return 0;
	}
	int query(int x){
		x=n-x+1;
		int ans=0;
		for(int i=x;i;i-=lowbit(i))ans+=t[i];
		return ans;
	}
}
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
};
int main(){
	freopen("beacon.in","r",stdin);
	freopen("beacon.out","w",stdout);
	n=read();
	for(int i=1;i<=n;i++)d[i]=read();
	for(int k=3;k<=n;k++){
		int i=k-2;
		int j=i+d[i];
		int l=2*j-i+1;
		l=min(l,n+1);
		a[l].push_back(j);
		bit::insert(min(j,n),1);
		for(int o=0;o<a[k].size();o++){
			bit::insert(min(a[k][o],n),-1);
		}
		f[k]=bit::query(max(k-d[k],1));
	}
//	for(int i=1;i<=n;i++)printf("%d ",f[i]);
//	printf("\n");
//	return 0;
	for(int i=1;i<=n;i++)ans^=f[i];
	printf("%d\n",ans);
}