Trie树

什么是Trie

我们现在有很多很多的单词，想要记录下来并对它们进行各种神奇的操作(比如求最长前缀以及字符串匹配什么的)，这时候我们就要用\(trie\)来记录。
煮个栗子：
我们现在要记录下\(qwqwqwq\) ，\(qwqwqaq\) ，\(qqqqq\)这三个单词，建出来的\(trie\)就长这样

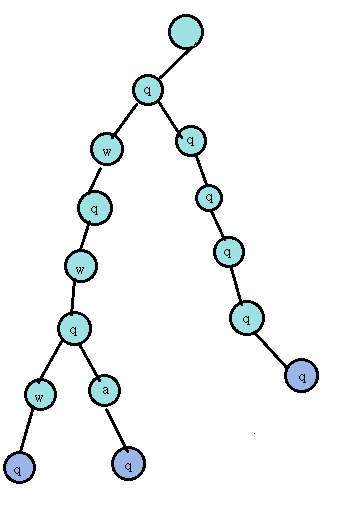
显然这棵\(trie\)要支持插入，那么怎么插入呢？

插入操作

在上面的\(qwqwqwq\)和\(qwqwqaq\)中可以看出来它们共用了\(qwqwq\)这个部分。新插入字符串也是如此。从根开始遍历，不断寻找当前点中和下一个要插入的字符相同的儿子，如果没有就新建。然后跳到这个儿子上，重复此过程。插入完所有字符后，在当前所在的点打上结尾标记（就像上图中蓝色的那样）

在写代码的时候，用\(ch[i][j]\)表示节点编号为\(i\),表示的字符为\(j\)的子节点的编号
代码：

void add()//这里已经在主函数里输入当前要插入的字符串ms
{
	int len=strlen(ms);
	int now=1;
	for(int i=0;i<len;i++)//挨个字符插入
	{
		int ch=ms[i]-'a';
		if(!trie[now][ch])
			trie[now][ch]=++cnt;//找不到就新建
		now=trie[now][ch];//寻找表示字符相同的子节点	
	}
	en[now]++;//en[i]记录以i节点为结尾的字符串的个数
}

关于查询因题而异
板子题

Trie的一些应用

1.字符串排序

直接从左到右遍历就好了

2.词频统计

找一下最大的\(en[i]\)

3.\(AC\)自动机(\(NOIP\)不考)

\(trie\)上\(kmp\)

4.求给出的所有串中某个前缀的出现次数

01 Trie

顾名思义，01 \(trie\)上的点代表的字符只有0和1，插入的方式和上面的是一样的。

这个东西在处理异或问题时十分管用。

煮个栗子

假设现在给你\(n\)个数，这\(n\)个数两两异或，求最大的异或值。

暴力\(O(n^2)\)。

考虑一个数与其他数的最大异或值，可以采用贪心的思想每次都走与这个数当前位相反的(如果没有就只能走相同的了)。

不过这玩意大概是省选才会考的

今年\(Day 2\ T2\)就是对树进行操作再加\(01\ trie\)

插入：
insert(int x){
	int now=0;
	for(int i=31;i>=0;i--)
	{
		int v=(x&(1<<i))>>i;
		if(!ch[now][v]){
			ch[now][v]=++cnt;
		}
		now=ch[now][v];
	} 
	en[now]++;
}

板子题：最大异或路径

某鸽子咕咕咕了好久.jpg