静态主席树（luogu可持久化线段树板子1）

主席树是个啥

任务：给定一个序列，多次询问区间\([l,r]\)中第\(k\)大的数。
暴力想法：每次都把区间排个序，爆扫一遍
复杂度：上天\(O(n^2logn)\)
显然这太不优雅了。
我们先考虑不是求\(l\)到\(r\)的第\(k\)大值，而是求\(1\)到\(r\)的第\(k\)大值应该怎么求。我们可以建一棵权值线段树，记录数出现的次数，然后递归解决。
那么对于每一个\(i\),都可以建一棵权值线段树。先不考虑空间问题，来看看怎么求\(l\)到\(r\)的第\(k\)大值。现在我们有\([1,l-1]\)的权值线段树和\([1,r]\)的权值线段树，那么我们在递归的时候只需要减去\([1,l-1]\)中出现的次数就可以了。
如果用这个思路，我们就要开\(n\)棵权值线段树，but
很显然空间炸了。
我们考虑\([1,i]\)的线段树和\([1,i+1]\)的线段树有什么不同。发现\([1,i+1]\)的线段树比\([1,i]\)的线段树仅仅多了\(log_i\)个节点，也就是说有很多重复节点。如果我们利用这些重复节点，就可以省下很大的空间。这就是传说中的主席树(可持久化线段树)

如何利用重复节点

我们边煮举栗子边看
现在我们有\([1,4]\)的线段树，我们想建一棵\([1,5]\)的线段树

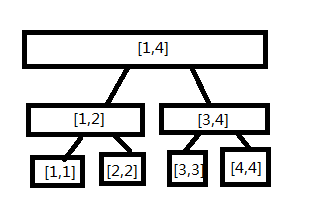
\([1,5]\)的线段树多了\([5,5],[3,5],[1,5]\)的节点

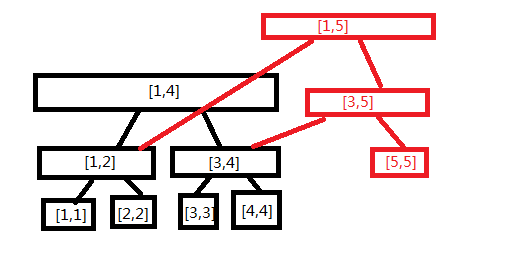
嗯，就是这样
可以发现我们在建树的时候不是一开始就建好的，而是不断添加节点。\(i\)每增加\(1\)，节点数就增加\(log_i\)个，增加的总结点的数量级是\(nlog_n\),故空间复杂度是\(nlog_n\)
看看代码吧

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const int inf=2147483647;
typedef long long ll;
template <class T> 
inline void read(T &x)
{
	char ch=getchar();
	x=0;bool f=0;
	while(ch<'0'||ch>'9')
	{
	    if(ch=='-')f=1;
	    ch=getchar();
	}  
	while(ch>='0'&&ch<='9')
	{
		x=x*10+(ch^48);
		ch=getchar();
	}  
	if(f) x=-x;
}
const int N=200009;
int n,m,a[200009],b[200009],w,lc[200009],bh;//a,b为离散化数组，lc[i]表示[1,i]这棵树的根的编号
struct zxs{
	int val,ls,rs;//记录出现次数，左儿子编号，右儿子编号
}sum[N<<5];//主义空间
void bld(int &owo,int l,int r)//先开一棵空树
{	
    owo=++bh;
	if(l==r)
	{
		sum[owo].ls=0,sum[owo].rs=0;
		sum[owo].val=0;return ;
	}
	int mid=(l+r)>>1;
	bld(sum[owo].ls,l,mid);
	bld(sum[owo].rs,mid+1,r);
	sum[owo].val=0;
	return ;
}
int build(int k,int l,int r,int nw)//开新点,k表示与这个新点处于同一层的最后的一个点的编号,l,r表示权值，nw表示当前点离散化后的权值
{
	int ne=++bh;//新点的编号
	sum[ne].ls=sum[k].ls;sum[ne].rs=sum[k].rs;sum[ne].val=sum[k].val+1;
	if(l==r)
		return ne;
	int mid=(l+r)>>1;
	if(a[nw]<=mid) sum[ne].ls=build(sum[k].ls,l,mid,nw);
	else sum[ne].rs=build(sum[k].rs,mid+1,r,nw);		
	return ne;
}
int qry(int u,int v,int l,int r,int e)//u,v表示线段树编号的起始，终点，l,r表示权值，e表示第e个
{
	if(l==r) return l;
	int mid=(l+r)>>1,x=sum[sum[v].ls].val-sum[sum[u].ls].val;
	if(e<=x) return qry(sum[u].ls,sum[v].ls,l,mid,e);
    else return qry(sum[u].rs,sum[v].rs,mid+1,r,e-x);
}
int main()
{
	read(n);read(m);
	for(int i=1;i<=n;i++)
	 read(a[i]),b[i]=a[i];
	sort(b+1,b+1+n);
	w=unique(b+1,b+1+n)-b-1;
	for(int i=1;i<=n;i++)
	 a[i]=lower_bound(b+1,b+1+w,a[i])-b; 
	bld(lc[0],1,w);
	for(int i=1;i<=n;i++)
	 lc[i]=build(lc[i-1],1,w,i);
	while(m--)
	{
		int l,r,k;
		read(l),read(r),read(k);
		int x=qry(lc[l-1],lc[r],1,w,k);
		printf("%d\n",b[x]);
	} 
}