网络流之最短路径覆盖问题
最近肝网络流有点上头
其实就是想水博客不想做题
博客前废话完毕
作为\(luo\ gu\)经典的网络瘤24题之一当然要写个博客了
传送


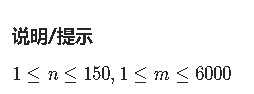
题目到底在说啥?
现在有一个DAG.选出图上任意条路径,每选出一条路径,该路径上的点被覆盖的次数+1,使得所有点都被覆盖且任意一个点只被覆盖一次。选出的路径的数量就是一个路径覆盖。最小路径覆盖就是最少的路径的数量。
举个简单的栗子
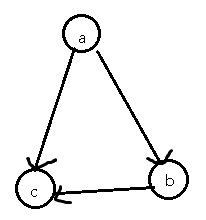
显然最短路径覆盖是1
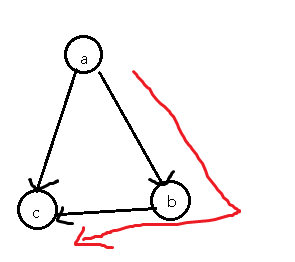
就是红色的路径辣
如果给我们的是一张十分复杂的图怎么办?
路径覆盖这东西最大也就是n-1对叭?(暴力的选出类似树一样的东西,它有n-1条边)
我们考虑让路径覆盖变小一点
如果我们选出来的边有a-->b和b-->c的边,那么它们就可以合并成一条路径,从而使答案-1
当然要注意如果此时还有b-->d的边,那么a-->b只能从b-->c和b-->d中选一个合并
那么最小路径覆盖就是把边不断合并,一直合并到无法再合并为止
显然我们得把这个东西和网络流联系一下(不然怎么叫网络瘤24题)
想到网络流可以搞二分图匹配
接着想到我们有拆点这个操作
拆点操作是个啥
就是把一个点拆成入点和出点两个点,出点的只有出度没有入度,入点只有入度没有出度。
说白了就是这个点出去的边从出点出,同时这个点作为终点的边是连向入点
搞完出点和入点之后发现这是一个二分图
有了这个神奇的操作,我们每次合并一条边,就是选出来一个匹配。我们要合并尽可能多的边,就是选出来尽可能多的匹配,也就是二分图最大匹配问题
求二分图最大匹配,可以用匈牙利算法这种好东西(还顺带记录了路径),but这里是网络瘤的世界,所以我们考虑用网络流搞。
上面已经搞定了建图(也就相当于搞定了网络流),接下来就是毒瘤的记录路径了
考虑到建图的时候入点的编号是点的真实编号+n,所以可以预处理ys(映射)数组,ys[i]为i点的真实编号(也就是说当i>n时,ys[i]=i-n)
同时考虑到网络流的原理,如果有一条边的残量(也就是dis)为0,则说明最终我们选择了这个匹配,也就是说与该边相连的点在同一条路径上。这样输出路径就可以用dfs实现。注意在dfs的时候也要考虑那些反向边。
直接贴代码叭
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const int inf=214748364;
typedef long long ll;
inline int read()
{
char ch=getchar();
int x=0;bool f=0;
while(ch<'0'||ch>'9')
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return f?-x:x;
}
int n,m,head[409],cnt=1,ans,s,t;
struct E{
int to,nxt,dis;
}ed[12009];
int dep[409],cur[409];
queue <int> q;
int ys[409];
bool vis[159];
inline void add(int fr,int to,int dis)
{
cnt++;
ed[cnt].to=to;
ed[cnt].dis=dis;
ed[cnt].nxt=head[fr];
head[fr]=cnt;
}
inline bool bfs()
{
for(int i=1;i<=2*n+2;i++)
dep[i]=0;
for(int i=1;i<=2*n+2;i++)
cur[i]=head[i];
dep[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(ed[e].dis&&!dep[v])
{
dep[v]=dep[u]+1;
q.push(v);
}
}
}
return dep[t];
}
int dfs(int now,int in)
{
if(now==t)return in;
int out=0;
for(int e=cur[now];e;e=ed[e].nxt)
{
cur[now]=e;
int v=ed[e].to;
if(ed[e].dis&&dep[v]==dep[now]+1)
{
int ret=dfs(v,min(in,ed[e].dis));
ed[e].dis-=ret;
ed[e^1].dis+=ret;
in-=ret;
out+=ret;
if(!in) return out;
}
}
return out;
}
inline void dinic()
{
int ret;
while(bfs())
{
ret=0;
while(ret=dfs(s,20000000))ans+=ret;
}
}
//上面全是网络流
void lj(int u)//路径不是辣鸡 !!!
{
printf("%d ",u);
vis[u]=1;//vis记录是否已经输出
for(int e=head[u];e;e=ed[e].nxt)
{
int v=ed[e].to;
if(v==s||v==t)continue;//这里注意不考虑自己加的超源,超汇
if(!ed[e].dis&&!vis[ys[v]])
lj(ys[v]);
}
}
int main()
{
n=read();m=read();s=n*2+1;t=n*2+2;
for(int i=1;i<=m;i++)
{
int fr=read(),to=read();
add(fr,to+n,1);add(to+n,fr,0);
}
for(int i=1;i<=n;i++)
add(s,i,1),add(i,s,0);
for(int i=n+1;i<=2*n;i++)
add(i,t,1),add(t,i,0);
for(int i=1;i<=n;i++)
ys[i]=i;
for(int i=n+1;i<=2*n;i++)
ys[i]=i-n;
ys[s]=s;ys[t]=t;
dinic();
ans=n-ans;
for(int i=1;i<=n;i++)//这里就不从超源开始考虑了qwq
{
if(!vis[i])
{
lj(i);
printf("\n");
}
}
printf("%d",ans);
}





