洛谷P2456 二进制方程
题目描述
一个形如:
X1X2…Xn=Y1Y2..Ym
的等式称为二进制方程。
在二进制方程的两边:Xi和Yj (1<=i<=n;1<=j<=m)是二进制数字(0、1)或者一个变量(小写字母)。每个变量都是一个有固定长度的二进制代码,他可以在等式中取代变量的位置,称这个长度为变量的长度。为了解一个二进制方程,需要给其中的变量赋予适当的二进制代码,使得我们用他们替代等式中的相应的变量后(等式的两边都变成二进制代码),这个等式成立。
编程任务:
对于每一个给出的方程,计算一共有多少组解。已知变量最多有26个(26个英文小写字母),且等式的每一端的数字和变量的长度之和不超过10000。
输入格式
第一行:k(k<=26,变量的个数,规定使用小写英文字母中的前k个字母作为变量,如k=5,则变量a,b,c,d,e)。
第二行:k个正整数,中间用一个空格隔开,依次代表k个变量的长度。
第三行:等式左边的表达式。
第四行:等式右边的表达式。
输出格式
等式中出现的变量共有多少组解。
输入输出样例
2 4 2 1b1 a
4
5 4 2 4 4 2 1bad1 acbe
16
说明/提示
样例一:4组解
1 、a=1001; b=00
2、 a=1011; b=01
3、 a=1101; b=10
4、 a=1111; b=11)
样例二:K=5,变量:a,b,c,d,e。长度分别为:4 2 4 4 2。等式是:1bad1= acbe
输出16,即变量a,b,c,d,e共有16组解。
先来一波思路叭(代码实现先鸽着)
我们可以手动解一下样例2
把左右两边的式子表示出来,其中确定是1/0的地方写上具体数字,不确定的位空着
同一字母用同一颜色表示

第一行是左边的式子,第二行是右边的式子
秉着左右式子一样(上下对应位置一样)的原则,我们开始填数

然后发现同一字母的同一位置也必须一样
继续填
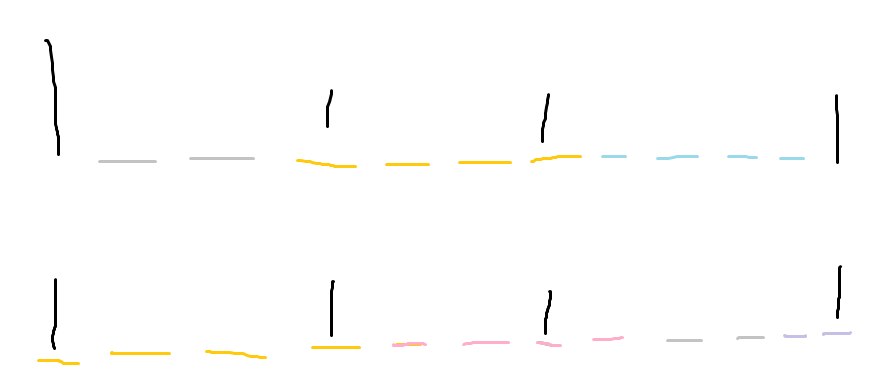
剩下的位置似乎可以填啥都行了叭
我们填填试试
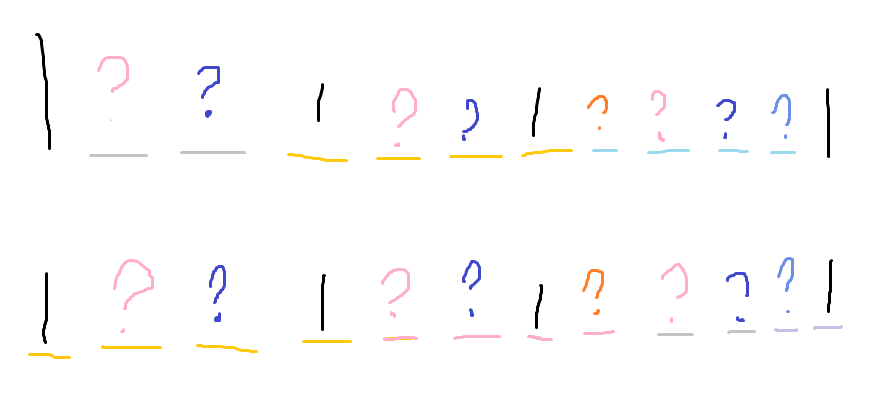
同一颜色的问号的位置只能填同一个数
这样我们要求的就是2问号的颜色总数
那么怎么维护填同一个数的那些位呢?
当然是建边然后dfs,用vis数组标记辣!!!!
神奇的并查集踩爆上面(无论是码量还是运行时间)
实现:对于每个字母的每一位都用不同的数来标记,同时并查集维护这些用来标记的数。
/*stO ybr Orz*/ #include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return f?-x:x; } int cn,sum,k,p[27],x[10005],y[10005],fa[100009];//p[i]:第i种颜色第一位的标记数字 int sa[1000009],lens=1;//高精用的 char s[10005]; int find(int x) { if(fa[x]==x)return x; fa[x]=find(fa[x]); return fa[x]; } void cheng(int k) { sa[1]*=k; for(int i=2;i<=lens;i++) { sa[i]=sa[i-1]/10+sa[i]*k; sa[i-1]%=10; } while(sa[lens]>=10) { lens++; sa[lens]=sa[lens-1]/10; sa[lens-1]%=10; } } int main() { k=read(); p[1]=2; //给1和0留下标记数字 for(int i=2;i<=k+1;i++) { int xw=read(); p[i]=p[i-1]+xw; sum+=xw;//记录一共有多少个不同的位 } scanf("%s",s+1); int len=strlen(s+1); for(int i=1;i<=len;i++) { if(s[i]>='a'&&s[i]<='z') { int c=s[i]-'a'+1; for(int j=p[c];j<p[c+1];j++)x[++cn]=j;//x[i]是第一个串第i位的标记数字 } else x[++cn]=s[i]-'0';//如果是数字的处理方法 } scanf("%s",s+1); len=strlen(s+1); int qwq=cn;cn=0; for(int i=1;i<=len;i++) { if(s[i]>='a'&&s[i]<='z') { int c=s[i]-'a'+1; for(int j=p[c];j<p[c+1];j++)y[++cn]=j; } else y[++cn]=s[i]-'0'; } if(cn!=qwq) { printf("0");return 0; } for(int i=1;i<=p[k+1];i++) fa[i]=i; for(int i=1;i<=cn;i++) { int dx=find(x[i]),dy=find(y[i]);//因为两个串的上下对应位置相同,所以合并它们 if(dx+dy==1)
{
printf("0");return 0;
}
if(dx!=dy) { fa[max(dx,dy)]=min(dx,dy); sum--;//合并之后不同的位-- } } sa[1]=1; for(int i=1;i<=sum;i++) cheng(2);//O(n)爆乘(省码量) for(int i=lens;i>=1;i--) printf("%d",sa[i]); }


