图论&线性基(?)(8.12)

边没有负权,最短路最多只有n条边
很暴力的思想:
先跑一遍最短路,找出最短路上的边,枚举每条边,翻倍,放进原图再跑一遍。取最大值

好熟悉啊
分层建图,建k层
每层内部是原图
若原图中u到v有连边,则由本层的u向下一层的v连一条边权为0的单向边
当然对于某些duliu的图(比如边数<k),用不完k次机会,所以我们还要在本层的u向下一层的u连一条边权为0的边
跑第一层的1到第k层的N的最短路
可能是唯一的代码:

#include<bits/stdc++.h> #define ll long long using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } int n,m,k,head[2000009],cnt; struct Ed { int to,dis,nxt; }edge[20000009]; void add(int fr,int to,int dis) { cnt++; edge[cnt].to=to; edge[cnt].dis=dis; edge[cnt].nxt=head[fr]; head[fr]=cnt; } int dis[2000009]; priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q; bool vis[2000009]; void dij() { q.push(make_pair(0,1)); memset(dis,0x3f,sizeof(dis)); dis[1]=0; while(!q.empty()) { int now=q.top().second; q.pop(); if(vis[now])continue; vis[now]=1; for(int e=head[now];e;e=edge[e].nxt) { if(dis[now]+edge[e].dis<dis[edge[e].to]) { dis[edge[e].to]=dis[now]+edge[e].dis; q.push(make_pair(dis[edge[e].to],edge[e].to)); } } } } int main() { n=read(),m=read(),k=read(); for(int i=1;i<=m;i++) { int fr=read(),to=read(),dis=read(); for(int j=1;j<=k+1;j++) { add((j-1)*n+fr,(j-1)*n+to,dis); add((j-1)*n+to,(j-1)*n+fr,dis); add((j-1)*n+fr,j*n+to,0); add((j-1)*n+to,j*n+fr,0); } } int ans=214748364; dij(); for(int i=1;i<=k+1;i++) ans=min(ans,dis[n*i]); printf("%d",ans); }

暴力:建n2条边
但一定是有些边是没有用的
按照x排序
我们发现如果 x1<x2<x3,则x1-->x2的边权+x2--->x3的边权≤x1--->x3的边权
所以在两个相邻的点之间建边,不相邻的就不建
然后对y排序,也是这样建边
跑di就好辣j

n<1e5:
如果我们有一个确定的最小边,则可用的边集的边权就必须比最小边大
我们可以考虑kruskal,枚举最小边,然后跑kruscal,当u和v连通的时候就停止
不断枚举最小边
数据duliu的出到1e5:LCT
什么是LCT?
说人话:
枚举最小边(从大到小),维护当比当前边大的边所构成的最小生成树
枚举到下一条边时,把刚才枚举的边加进去,如果构成环则删掉换上的最大边
每次都看看最大边和当前边的比值,取最小
bzoj 1821

二分?
二分答案是mid,把比mid小的边放在部落的内部。把这些边拿出来,看连通块的个数是否>=k。
MST:
这个题要求选出k个联通块,然后剩下的边的最小值尽可能大
要做到这一点,边权最小的边肯定要让它在部落中间,而不是连接部落
所以我们从小到大选边,让这些边来连接部落内部
当形成k个连通块(k个部落)的时候,立即停止。
还没有选的边中最短的边就是答案
不过这里我们是选n-k条边

说中文:
你有n个座位排成一行,会有Q个座位预定操作,每个操作会预定[l,r]内的座位。把这些座位输入系统,每次只能输入一个。每次输入,系统会自动会把[l,r]内没有被分配出去的座位分配给这个预定。求获得座位最少的人可以获得的最大的座位数

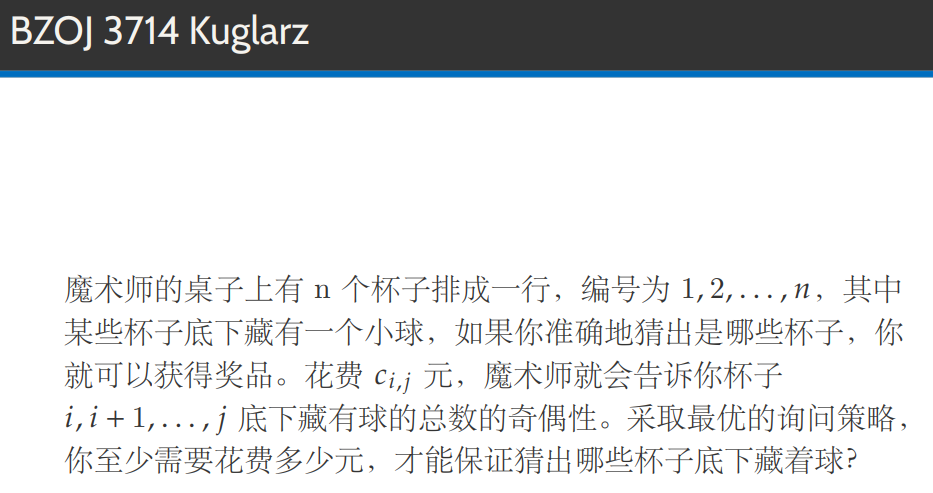
推理出s1~s2,s1~s3,s1~s4...s1~sn即可推理出答案
设s[i]为1到i的前缀和(模2意义下)(也就是异或和)
边界:s[0]=0
询问[l,r]:可以知道s[r]和s[l-1]的奇偶性是否相同
如果a和b奇偶性相同,b和c奇偶性相同,则a和c奇偶性相同
所以奇偶性有传递性,就像树上的点可以连通一样
因此,知道[l,r],就相当于由s[l-1]到s[r]连一条边
最后我们要推理出所有的s[i],也就是要保证通过选边让每个s[i]都与s[0]连通
这样就是求最小生成树
贪心策略:去找距离当前点最近的加油站
证明:
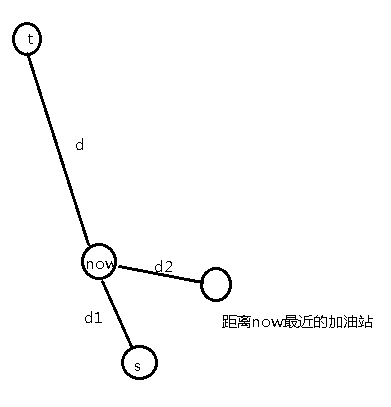
now不是加油站
设d1>=d2
b-d2>=b-d1 所以先去加油站肯定是要优的
如果d1<d2
那d2通向的那条边就不是距离now最近的加油站了(因为s比那个点更近)
所以,对于不是加油站的点,先去最近的加油站总是最优的,并且对于任意一个不是加油站的点,如果到达那里的油量>d,那么去加油站之后回来的油量也>d
这样我们就是不停的奔波在加油站之间,所以我们希望经过加油站的路径最大的那一条最小
kruskal可以帮我们做到这一点
problem:
对于那些在非加油站之间的边怎么办?
找到左边最近的加油站,右边最近的加油站,连一条边(边权就是这两个加油站之间的最短路)
接下来kruskal搞最小生成树

先跑Elaxia的最短路图,再跑w的最短路图(都是有向边),然后把公共路径找出来,此时一定是个DAG
然后在DAG上拓扑DP最长路径
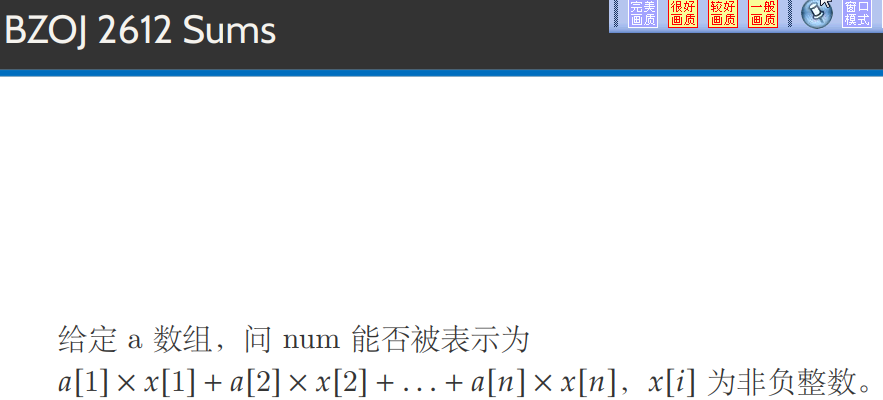
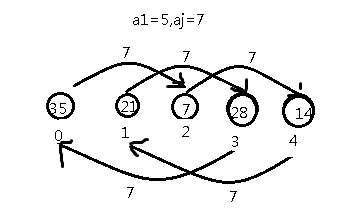
设t%a1=k
若k可以被凑出来,则%a1==k,且>=k的所有t都能被凑出来
这样我们只需要求出来所有 (t+a[j])mod a1能搞到的最小的k就搞定这个题了
我们可以开a1个点,如果我们要加a[j],则视为在点x,可以花费a[j]的代价,到达(x+a[j])%a1这个点
搞个图感(xing)性(gan)李姐一下
线性基:
一堆数,求基底(基底不能异或出0)
基底:就是一些能异或出其他数的数
基底就是一个拟阵
与图论的关系:
n个点--->n位的二进制数
边的表示:连接哪两个点,对应的那两位上就是1
判链:所有的边异或起来:只剩头,尾
判环:异或起来是0
无向生成森林:
异或起来只剩头,尾
倍增floyd
普通的floyd:
(伪代码,a和b是数组,其中a是邻接矩阵)
void floyd(a,b) { for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) c[i][j]=min(a[i][k]+b[k][j]); }
这时是经过两条边的最短路
经过3条边:
在上面的基础上再用c和a来一遍
经过k条边:a floyd a floyd a floyd a.........
这样看起来很蠢很不优雅对不对
这里是有结合律的,所以我们可以这么加括号
((a floyd a) floyd (a floyd a)) floyd ..........
就类似快速幂的写法
伪代码:
auto pow(a ,int p)//求a的p次方 { juzhen x=E //这里是伪代码辣) while(p) { if(p&1) x=floyd(x,a); a=floyd(a,a); p>>=1; } return x; }
常见问题:经过边数最少的负环
暴力:k一点一点的加
经过思考:二分k
再思考思考:k:看220行不行?219行不行?.....






