单调队列小记——————滑动窗口

一些废话：

纪念hin久以前gellygoat大佬给我们讲了以后窝就再也没动过的单调队列

qbxt的电脑编译一次9s+可海星

f10真好用

题目传送

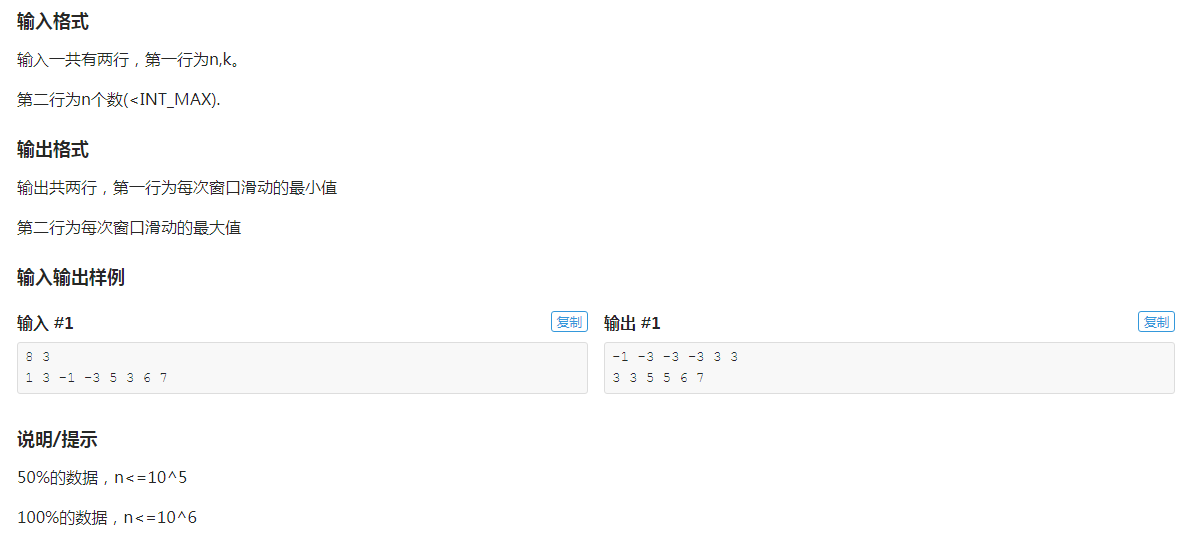
数据看起来能用线段树卡过？

这道题作为单调队列的板子题当然是用单调队列了

这里呢，我们设两个单调队列（dalao是用一个，但我不是dalao,只会用两个）

既然是单调队列，队列里面的元素肯定是单调的。但是注意单调队列不是优先队列

单调队列其实是一个双端队列

先贴一下双端队列常用的函数

插入：

从队头插入:q.push_front();

从队尾插入:q.push_back();

双端队列的某一元素前插入一个元素x:iterator insert(iterator it,const T& x)

双端队列中某一元素前增加n个相同的元素x:void insert(iterator it,int n,const T& x)

删除：

删除队头的元素：q.pop_front()

删除队尾的元素：q.pop_back()

清空队列:q.clear()

删除某一元素：Iterator erase(iterator it)

更多用法见这里

拿维护最小值的那个队列举例好了

我们维护队头是当前区间的最小值。

如果当前队列的第一个数的下标小于now(当前滑块的左端点),就说明它该退役了，pop掉（注意队列要非空）

我们从队尾插入新的数。如果队尾当前的数比a[x](要插入的数)大，此时队尾的数的下标一定比x小，也就比a[x]更早失去效果。由此看来，当前队尾的数不可能成为最小的数的候选者，所以我们把它pop掉

经过上面两轮pop,就可以将a[x]放到队尾了

细节什么的见代码吧

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
inline int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int now,n,k,a[1000009],mi[1000009],ma[1000009],cnt;
struct dl{
    int xb,zhi;//队列是结构体类型，记录下标和数的值
    dl(int xx,int yy):xb(xx),zhi(yy){}//构造函数
};
deque<dl> qma,qmi;//qma维护最大值，qmi维护最小值
void pshmax(int x)
{
    while(!qma.empty()&&qma.front().xb<now) qma.pop_front();//注意队列非空（RE警告）
    while(!qma.empty()&&qma.back().zhi<a[x])qma.pop_back();
    qma.push_back(dl(x,a[x]));

}
void pshmin(int x)
{
    while(!qmi.empty()&&qmi.front().xb<now) qmi.pop_front();
    while(!qmi.empty()&&qmi.back().zhi>a[x])qmi.pop_back();
    qmi.push_back(dl(x,a[x]));
   
}
void luangao()
{
    for(now=2;now+k-1<=n;now++)//加的是k-1啊k-1
    {
        pshmin(now+k-1);pshmax(now+k-1);
        mi[++cnt]=qmi.front().zhi;
        ma[cnt]=qma.front().zhi;
    }
}
int main()
{
    n=read();k=read();
    for(int i=1;i<=n;i++)
     a[i]=read();
    qma.push_back(dl(1,a[1]));
    qmi.push_back(dl(1,a[1]));
    for(int i=2;i<=k;i++)//先手动处理[1,k]这个区间
     {
         pshmax(i);
        pshmin(i);
     }
     ma[1]=qma.front().zhi;
     mi[1]=qmi.front().zhi;
     cnt=1;
    luangao();
    for(int i=1;i<=cnt;i++)
     printf("%d ",mi[i]);
    printf("\n");
    for(int i=1;i<=cnt;i++)
     printf("%d ",ma[i]); 
}