dp基础大概 (8.6)

 一些前言：

据说动态规划会用排序，数据结构来进行乱搞优化操作

动态规划滴核心是个啥呢？状态表示和状态转移

设状态：哪些因素会影响到最终答案，就把哪些因素用数组的维度表示出来

要充分描述，也要简洁

举个例子

计算从(1,1)走到(x,y)的方案数：

走到任意一个(p,q),只能从(p-1,q)和(p,q-1)走过来

那dp[x][y]=dp[x-1][y]+dp[x][y-1]

例一：

最长上升子序列

这个比较简单

dp[i]表示以a[i]为结尾的最长上升子序列的长度

dp[i]=max{dp[j]}+1(a[j]<a[i]&&j<i)

复杂度O(n²)

更秀一点的O(nlogn)做法：

len记录当前的最长上升子序列的长度，d[i]记录当前找到的最长上升子序列的第i项，若a[now]≤d[len],则找到第一个d[j]>a[now]的j,令d[j]=a[now],否则len++,d[len]=a[now],最后的len是最终答案,但d数组不一定是真正的最长上升子序列

dp[i][j]表示前i个位置用j个乘号的最大值

cnt(i,j)表示原数字串第i个数字到第j个数字所组成的数

dp[i][j]=max(dp[i][j],dp[k][j-1]*cnt(k+1,i))

挂饰：

看起来像个贪心（大雾）

那就排个序

按照Ai从大到小排

why?

因为挂钩越多，能挂的东西就越多

dp[i][j]=max(dp[i-1][j],dp[i-1][max(j-a[i],0)+1]+b[i])

蓝字部分是挂第i个挂钩的喜悦值

看蓝字部分的第二维，为什么+1要写在外面呢？

①：当j-a[i]+1<0时，j-a[i]肯定小于0，这时候考虑j-a[i]+1的状态是没有意义的，直接考虑手机上只有一个挂钩的情况

②：当j-a[i]+1==0时，那说明挂上i，就没有挂钩了，并且挂i只需要一个挂钩，也就是说之前手机上只有一个挂钩。如果我们写成max(j-a[i]+1,0),此时是转移到之前手机上没有挂钩的状态，是不对滴。

综上，+1要写在外面

最终答案：max{dp[n][i]}(0≤i≤n)

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
inline int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int n,dp[2010][2010];
struct G{
    int a,b;
}g[2010];
bool cmp(G x,G y)
{
    return x.a>y.a;
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    g[i].a=read(),g[i].b=read();
    sort(g+1,g+1+n,cmp);
    memset(dp,0xcf,sizeof(dp));
    dp[0][1]=0;dp[0][0]=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=n;j++)
        {
            dp[i][j]=max(dp[i-1][j],dp[i-1][max(j-g[i].a,0)+1]+g[i].b);
        }
    }
    int ans=0xcfcfcfcf;
    for(int i=0;i<=n;i++)
     ans=max(ans,dp[n][i]);
    printf("%d",ans); 
}

（手机好沉ρωρ）

洛谷P1233 木棍加工

看起来像求最长不上升子序列个数，但是这似乎是二维的

那我们按照l从大到小排序，再看w中有多少个不上升子序列的最少的数量

那怎么求最少的不上升子序列的数量？

dilworth定理（翻译成人话版本）：

 最少的不上升子序列的数量就是最长上升子序列的长度（似乎在导弹拦截里面见过）

why?

度娘大概知道

 

P1091合唱队形

 nlogn做法qwq(导弹拦截的做法)

辣么另一种是什么呢？

我们回顾求最长上升子序列的时候,我们要找最大的dp[j],使得a[j]<a[i]

我们换个角度

就是找最大的k，使得dp[j]==k&&j<i&&a[j]<a[i]

很有可能有多个dp[j]==k

我们设置辅助数组h,h[k]为dp[j]==k中,最小的a[j]

同时h数组是单调递增的，所以查询时只要查询最大的小于a[i]的h数组的下标即可（二分查找）

为什么是单调递增的？

 

数据结构优化

暴力的不要不要的

据说是个二维偏序

用树状数组搞

维护前缀最大值

 

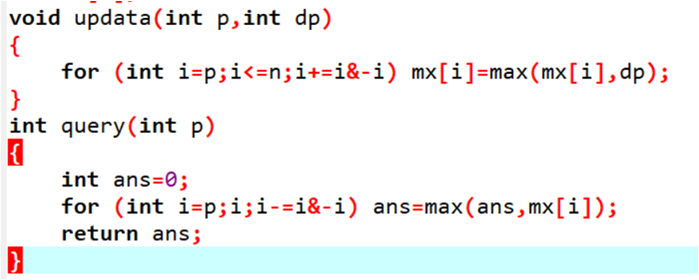
 如果要求公共子序列的个数怎么办

dp[i][j]:第一个串的前i个字母，第二个串的前j个字母的公共子序列的个数

若s[i]==t[j],选：转移到dp[i-1][j-1],不选：dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]  (这一块是重复的)

若不相等：dp[i-1][j]+dp[i][j-1]

数据范围你猜

好吧是复杂度是n²

先来个n⁴的暴力

dp[i][j]:A的前i,B的前j的balabala

然后搞一遍公共子序列的dp转移，如果小于末尾的数，就再找一遍

唉唉这为毛是四维的？？

在算dp[i][j]时要看dp[1][1],dp[1][2]...dp[1][j-1],dp[2][1]...一直到dp[i-1][j-1]

这样就是n²的

 

但是还是可以nb的继续优化

我们再设f[j]=max{dp[x][j]}(1<=x<=i-1)

当i到i+1的时候，只需要O(1)更改f[j]就可以了

这样总体就是O(n²)了

代码：

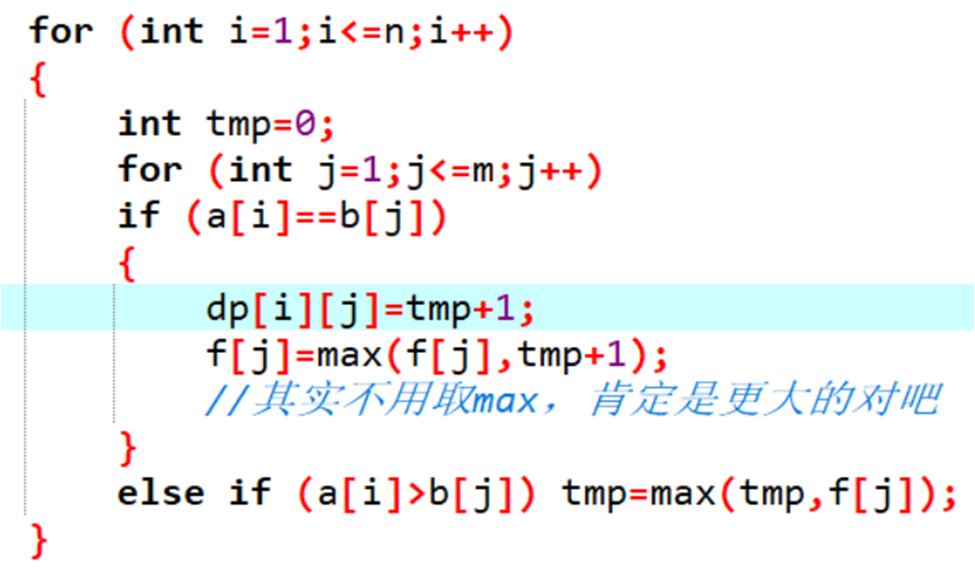
a[i]>b[j]是个什么鬼咧？

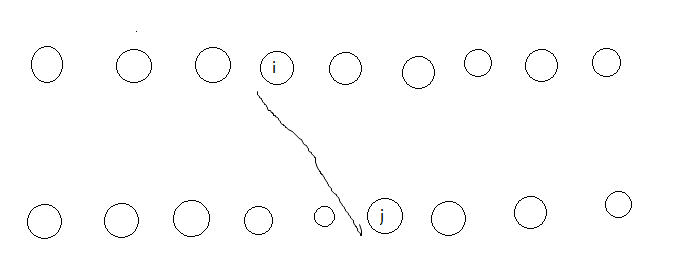
结合一下这张图。我们保证当前子序列的结尾是a[i],如果我们要更新后面的dp[i][j'],就是要求b[j']要小于a[i](当然，b[j]也要小于a[i])

tmp又是个啥？

tmp就是

红色圈里这一坨的最大值

好像似乎也许应该可能是一样的叭

 

 

dp and 容斥

zhx说小学学过（手动双关）

什么是容斥？加加减减乱搞一通

注意这里的n和m是10^8

算了我们简化一下10^6

肯定裸dp是药丸的

辣么我们用数学解决

容斥原理qwq

总路径-至少经过一个点+至少经过两个点-至少经过三个点+至少经过4个点.........

我们可以dp出容斥系数

奇数就减，偶数就加

 复杂度O(t²)

窝莫得听懂

溜

来我们看看记忆化搜索

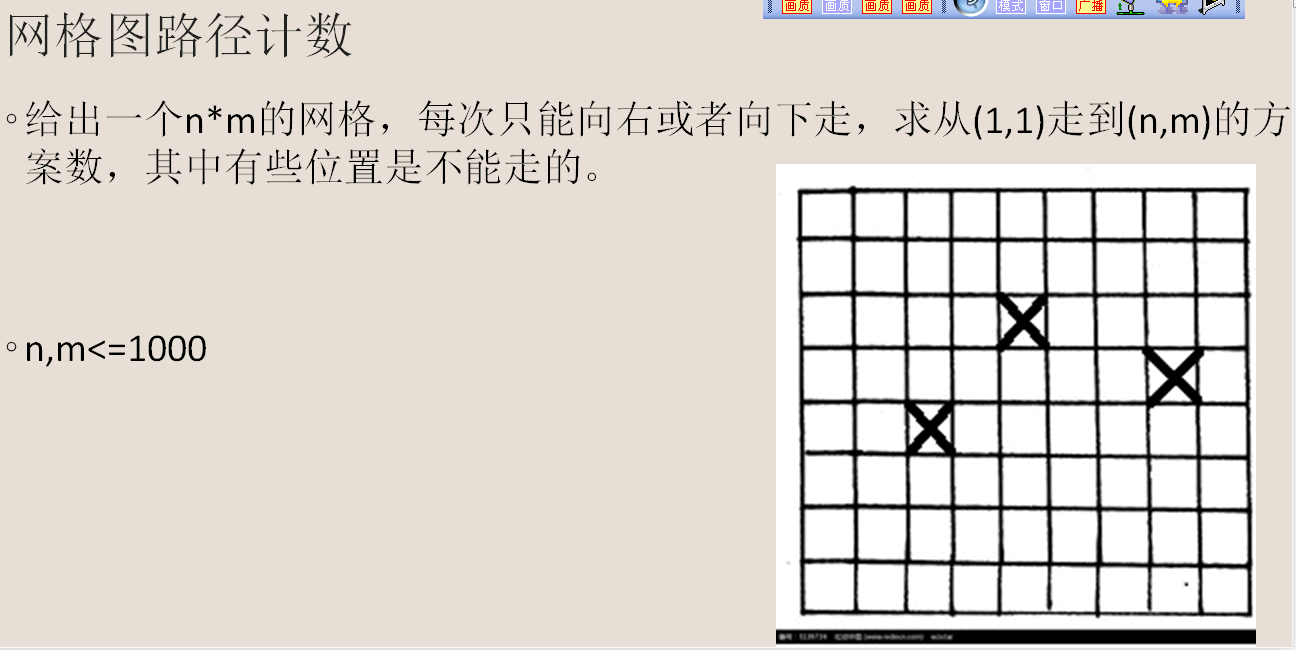
终于有一道数据范围人类的题了

如果我们只有一个dfs（x,y）表示从(x,y)走到(n,m)的距离

我们再dfs中可能多次调用同一个dfs(i,j),这样我们就可以把dfs(i,j)记下来，这就是记忆化搜索

 

做题步骤（雾

似乎搜索可以

哎参数不多唉

有的值重复计算了？？？

那就记下来

遇见duliu搜索顺序题怎么办

记忆化！！！（据说记忆化还有剪枝效果）

bzoj 3810

这是个好题

 

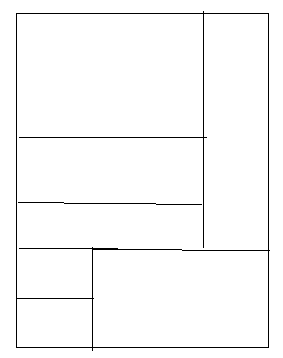
我们发现合法的一定有一条贯穿整个矩形的线

那我们就枚举贯穿线，算出左边差异度，右边差异度的最小值

设dp[i][j][4]为长为i,宽为j的矩形面对大海春暖花开状态

 

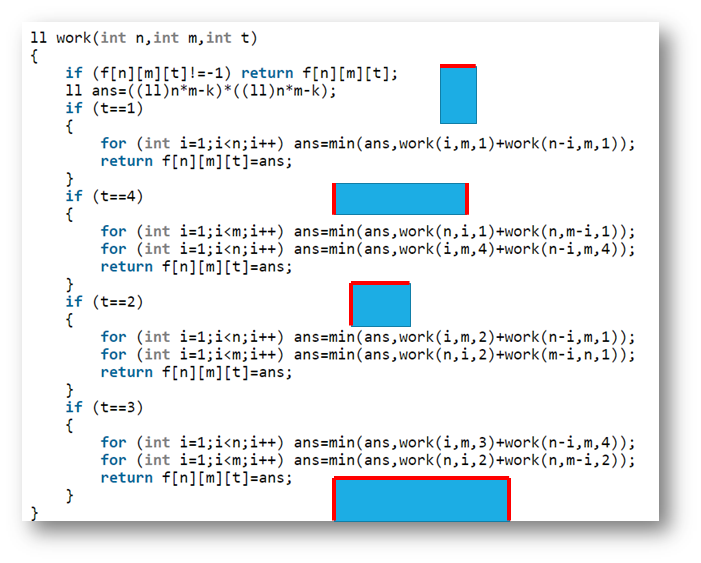
就是把一个矩形切成一堆小矩形

拓扑图dp

什么意思？

就是求从一个入度为0的点到达一个出度为0的点的方案数

dp[i]=∑dp[j](存在j到i的边)

我们可以边跑拓扑序，边计算dp[i]

最后出度为0的点的dp值的和就是答案

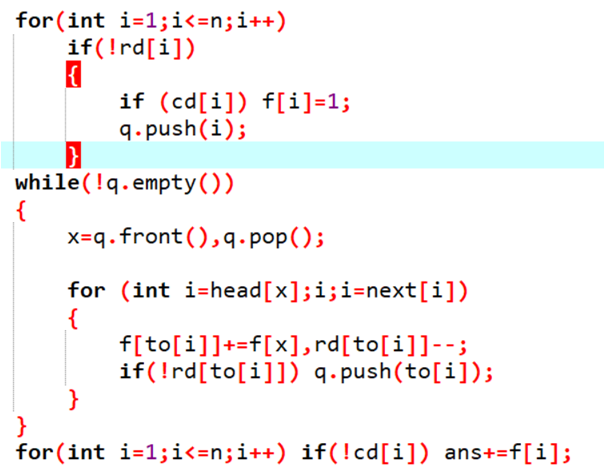
 最短路图怎么建？

如果dis[u]+len[edge[i]]=dis[v],那么edge[i]就在最短路径上

然后求到T的方案数

 

最大子矩阵

n⁴乱搞

其实如果数据保证都是正整数，那就是O(n²)的

正解：先对行进行组合，选取组合中的行，把每一列上的数加起来，就变成了一行数，然后求最大子段和

 所有组合中最大子段和的最大值就是答案

 举个例子叭

1 2 -10 6

2 -1 3 7

3 -5 9 8

这个矩阵一共有3行

那么行的组合有{(1),(2),(3),(1,2),(1,3),(2,3),(1,2,3)}

先对行1进行合并（其实不用合并），得到1 2 -10 6,跑最大子段和

行2和行3的省略辣（反正只有一行也没有什么可以合并的）

接下来才是真正的合并

取1,2行

1 2 -10 6

2 -1 3 7

同一列上的数字相加：

第一列：1+2=3

第二列：2-1=1

第三列：-10+3=-7

第四列：6+7=13

这样得到新的一行数： 3 1 -7 13，跑最大子段和

然后是对(1,3)(2,3)(1,2,3)这样搞，求出来所有的最大子段和中最大的那个就是答案

序列上设计dp

 

bzoj1003

f[i]表示前i天的最小中成本

可以套这个：

跑最短路，注意此处的最短路要保证在所有天里，起点和终点都可以互达

f[i]=min{f[j]+jl[j+1][i]*(i-j)+k}

bzoj1296

考虑只有一条木板

f[i][j]:刷到第i个格子，用了j次，最多正确粉刷的格子数

f[i][j]=max{f[k][j-1]+cnt(j+1,i)}(枚举k)

cnt:可以搞个前缀和，然后计算[j+1,i]中红色格子的数量，蓝色格子的数量，取max

再考虑有好多条木板

g[i][l]表示前i个木板一共刷了l次，最多的数量

g[i][l]=max{g[i-1][l-x]+f_i[m][x]|x≤m}

什么意思呢？枚举木板i粉刷的次数，找最大值

 

设左括号为+1,右括号为-1

则总和为0，任意前缀和≥0

dp[i][j]前i个位置的前缀和为j的方案数

 

 我们发现括号序列中的某些部分可以左右括号抵消

就像这样：(()))) ---------------> ))

回想一下打怪那个题

对于回血怪（a[i]-d[i]>0）,我们按照d[i]升序排序，对于扣血怪（a[i]-d[i]<0），我们按照a[i]降序排序

和这个题联系一下

我们把左括号当做+1，右括号当做-1，先进行化简（左右括号互相抵消）。化简完的序列的右括号一定在左括号的左边，数量用L[i]表示。左括号的数量用R[i]表示，要选出尽可能多的括号序列，也就是要打尽可能多的怪，就按照打怪的方法排序

f[i][j]表示前i个序列，+1,-1和为j时的最长长度，len[i]是排完序后第i个括号序列的最初长度

f[i][j]=max(f[i-1][j-L[i]+R[i]]+len[j],f[i-1][j])

ans=f[n][0]

一套有趣的题

卡特兰数？？？（不是记搜吗(っ°Д°;)っ）

对f[n]来说，第一个左括号一定有一个与之匹配的第一个右括号，那就枚举它们中间有多少对括号。若有i对，则贡献是f[i]*f[n-1-i]

f[n]=∑f[i]*f[n-1-i](0≤i≤n-1)

上面就是卡特兰数的公式辣

其他的卡特兰数的问法：

证明：

3：左右子树不一样，设左子数的大小为i，右子树的大小就是n-i-1，乘一乘还是原来的公式

4：这里其实是求的n+2条边的凸多边形

5：把往右走当做+1，往上走当做-1，保证前缀和为0，最后和为0，还是括号匹配问题

贪心的选取每个区间的最小值

这就是那个滑块的题辣

辣么怎么用单调队列优化这个题呢？

队头维护最小值，如果最小值的下标小于当前区间的左端点就pop掉，每次插入，如果前面的值比当前插入的值大，就pop掉，这样队头一直是当前区间的最小值辣

利用辅助数组优化

.....举个例子

dp[i][0][0]--------------->dp[i+1][1][1],且第一个串是ab?:

dp[i+1][1][1]=dp[i][0][0]*f[a][b][?][0][0][1][1]

说人话：f数组处理16种转移的系数

为毛是16种？

例一：合并石子

ρωρ

poj3280

dp[l][r]表示[l,r]变为回文串的最小值

如果s[i]≠s[j],考虑[i,j-1]和[i+1,j](删掉s[i]或s[j])

dp[i][j]=min(dp[i+1][j]+add[s[i]],dp[i+1][j]+del[s[i]],dp[i][j-1]+add[s[j]],dp[i][j-1]+del[s[j]])

若s[i]==s[j],则dp[i][j]=dp[i+1][j-1]

括号最大匹配

dp[i][j]表示[i,j]内最长的合法子序列

 考虑当前的括号是否匹配

没匹配：dp[i][j]=dp[i+1][j]

匹配：枚举和谁匹配

         若i和k匹配，则dp[i+1][k-1]是合法的，dp[k+1][j]还要选出一个合法的子序列

         所以dp[i][j]=max{dp[i+1][k-1]+dp[k+1][j]}

为毛上一个题不枚举和谁匹配呢？明明好像都是回文串的亚子

因为上一个题只能是回文串，但这个题可以是多个回文串拼起来

n≤100：枚举断点

n显然超过O(n³)允许的数据：一般来说是只考虑边界情况，不枚举断点           

bzoj1900

dp[i][j]:折叠区间[i,j]的最小代价

我们可以枚举断点唉

一个折叠的区间可能由两个区间拼接而成，就枚举断点

①：自身可以压缩：找循环节的长度k（hash）,dp[i][j]=dp[l][k]+2+区间长度/(k-l)+1

②：由可以压缩的子区间拼接而成,dp[i][j]=min{dp[i][k]+dp[k+1][j]}

 

环形问题

就是把一个环，断开成链，然后再把原来的链复制一遍接到后面

能量项链

如果它是个链：dp[i][j]=max{dp[i][k]+dp[k+1][j]+h[i]*h[k]*t[j]}

但是环可以搞出dp[4][3]这种操作，所以....

要环变链

 

dp[i][j]=min{dp[i][k]+dp[k+1][j]+gcd(a[i],a[j])}

似乎好像真的没什么东西