7.24考试

T1:

真.题面

时空限制：

看到时空限制，就知道这是一个脑洞题

我们联想异或运算：相同为0，不同为1

所以我们可以把所有的数异或起来，最后的数就是答案

#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int n,x,a;
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
       x=read();
       a^=x;
    }
    printf("%d",a);
}

T2:

虽然wz之前说过结论，虽然wz在考试的时候还提了一句，但是蒟蒻还是不知道结论并成功的只有暴力分。

调了半个上午一直wa,下午乱搞就a了?!!

打个表

发现有如下性质

 

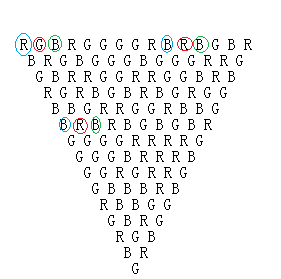
发现上排两个相同颜色的圈圈起来的字母做运算得到下面相同颜色的圈中的字母，同时两个相同颜色的圈之间的距离是不超过n的最大的3^k+1(硬核结论)

然后一直寻找不大于当前len的最大的3^k+1，做运算，减小len,直到len为1

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int n;
char a[10000009];
int three[15]={2,4,10,28,82,244,730,2188,6562,19684,59050,177148,531442,1594324,4782970};
void yu(char &q,const char &p)
{
    if(q==p)return ;
    if((q=='R'&&p=='G')||(q=='G'&&p=='R'))q='B';
    else if((q=='B'&&p=='G')||(q=='G'&&p=='B'))q='R';
    else if((q=='R'&&p=='B')||(q=='B'&&p=='R'))q='G';
    return ;
}
int main()
{
    n=read();
    scanf("%s",a+1);
    int len=n;
    while(len>1)
    {
        int now=0;
        for(int k=14;k>=0;k--)
        {
            if(three[k]<=len)
            {
                now=three[k];break;
            }
        }
        for(int i=1;i<=len-now+1;i++)
        {
            yu(a[i],a[i+now-1]);
        }
        len=len-now+1;
    }
    printf("%c",a[1]);
}

T3

当然了，电影券是没有的

整除key--->sum%k==0

这样我们就把问题转换成求%k之后为0的方案数了

我们联想到数字三角形2，里面让求%100之后的最大值。在那道题里面，我们又加了一维k,表示走到a[i][j],数字之和%100可不可能为k(是个bool数组),这里我们用类似的思路，f[i][j]表示当前搞到第i个数，数字之和%key==j的方案数

对于这一个数，有选和不选两种决策，不选：dp[i-1][j]。选：dp[i-1][(j-a[i])%key]

那dp[i][j]只需要把这两个加起来就好

初始条件：dp[0][0]=1(什么都不选，和为0，0%key=0,所以是1种方案)

最终答案：dp[n][0]

#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int n,key,a[1010];
ll d[1010][1010];
const int mod=1000000007;
int main()
{
    n=read(); key=read();
    for(int i=1;i<=n;i++)
     a[i]=read();
    d[0][0]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<key;j++)
        {
            int td=(j-a[i])%key;
            if(td<0)td+=key;
            d[i][j]=d[i-1][td]+d[i-1][j];
            d[i][j]=(d[i][j]+mod)%mod;
        }
    } 
    printf("%d",d[n][0]%mod);
}