7.19

如果不用树形dp,怎么做?
我们要使得士兵数量最少,那每个士兵要覆盖尽量多的节点

我们找到最深的叶子节点
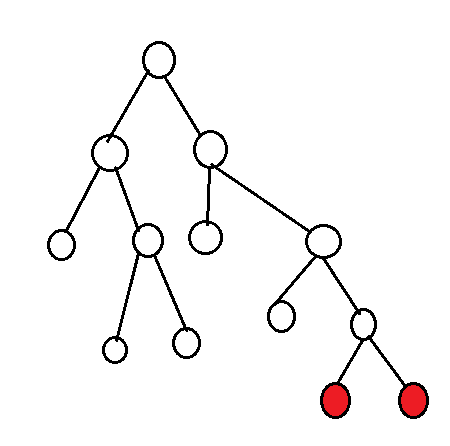
就是红色节点
我们以左边这个为例,如果要覆盖它,有4种放法

节点上的数字是第几种放法
显然情况四覆盖的节点最多
所以我们找到深度最深的节点,在它的爷爷上放上士兵,然后把它爷爷覆盖到的节点从树上删掉,然后重复这个操作,直到树为空
我们维护一个堆就可以做到删除节点
复杂度:O(nlogn)

染色方案是个什么意思?
如果我们有k种分组方案,每种方案都有M种颜色可以染,那最终的染色方案就Mk
举个栗子:N=6时,有4种分组方案,答案就是M的4次方
4种:1组,每组6人
2组,每组3人
3组,每组2人
6组,每组1人
所以有多少种方案就是看N有多少个因数
可以for一遍,O(√n)计算有多少个因子
然后快速幂计算Mk
增强版
在上面我们没有考虑人的顺序
所以我们考虑人的顺序
例子:
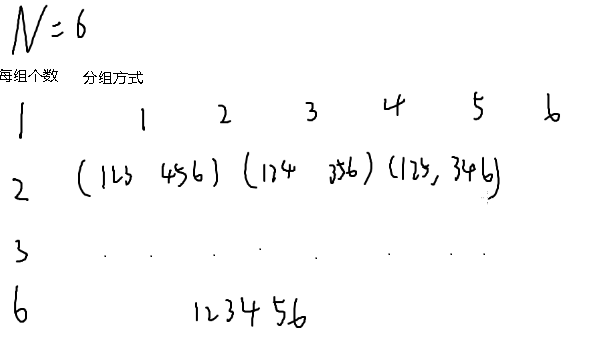
例如上面的分两组,就有了三种分法(其实不全)
怎么算?
假设我们现在要把这些人分成r组
第一组的方案数

第二组:这里因为第一组已经有N/r个人了,所以这里是N-N/r

第三组:因为又少了N/r个人,所以是N-2N/r

第n组:到最后只剩下N/r个人了
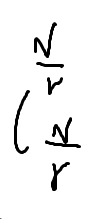
我们发现这里考虑了每组的顺序,所以我们还要在除以r!(例如这么算会有(123,456)和(456,123),但它们是同一种情况)
r!是r组的全排列
最终式子

那这玩意咋算呢?
把组合数拆一下
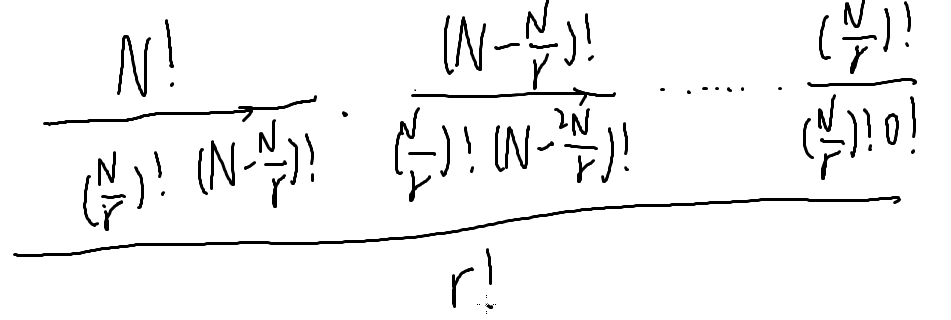
以上是按照组合数公式拆分
我们发现可以约分
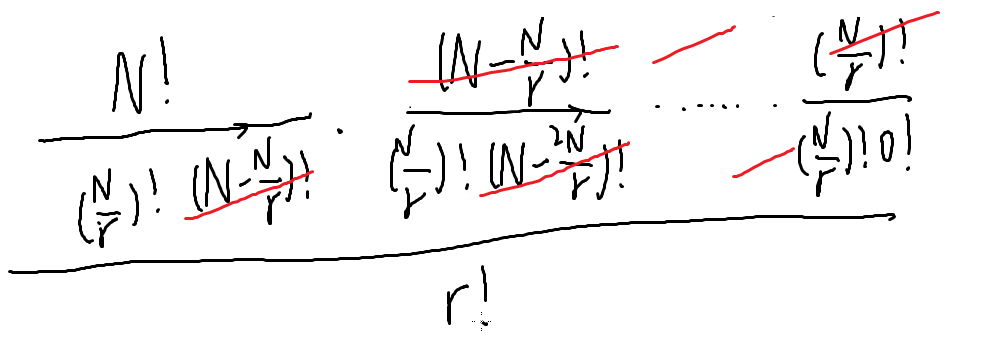
约分
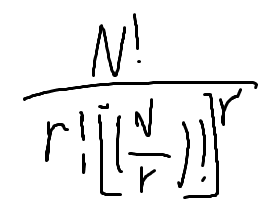
分r组的最终式子:
k的最终式子:
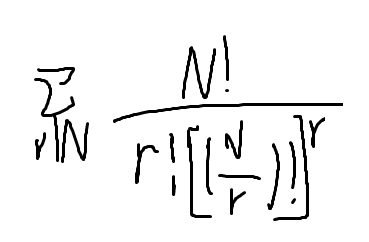
最后求的是Mk%(109-401)
那我们的k应该模多少呢?(109-401)?
我们想起推逆元时用的欧拉定理:

Mφ(1e9-401)≡1 (mod 109-401)
那Mk≡Mk%φ(1e9-401) (mod 109-401)
那问题就转换成了这样
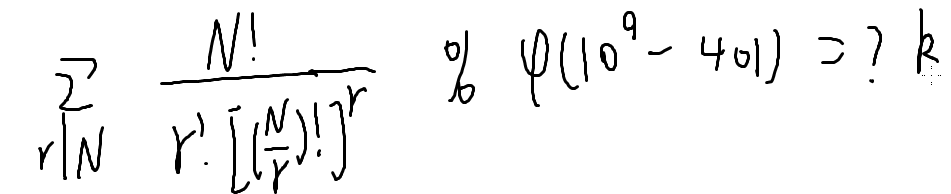
我们发现N!没法算(N是2*109)
这个题的模数很奇怪啊
它会不会是一个质数?
它的确是个质数
那φ(109-401)=109-402
进行一番分解质因数操作
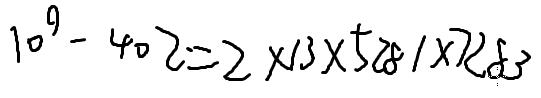
它的质因子都在10000以内,还不算太大
我们可以算N!mod这四个数分别是多少,然后乘起来,就是N!%109-402
问题进一步被转化为N!%一个数是多少
假设我们要算N!%13
我们把N!奋进成这样的形式
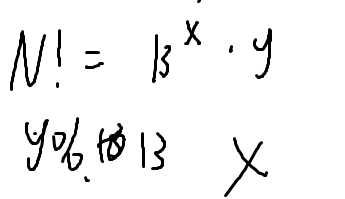
我们尝试把1~N中所有的数%13(对13的倍数特殊处理)
现在我们的模数很小,所以会有循环节(指1~N中的数%13之后会有循环节)

我们先不考虑13的倍数,那假设我们有q个循环节,则最后的答案(不包括13的倍数)
是(12!)q%13
我们再考虑13的倍数,把它们都拿出来,全部/13,把剩下的数%13计算

发现就是刚才的问题,那重复刚才的操作
这样就可以递归操作
复杂度log13N
大佬的式子(di就是要%的数)
n!=1*2..(di-1)*di*(di+1)*..*(q*di)*(q*di+1)...*n (mod di)
=((di-1)! mod di)^q*(n-q*di)!*q!*(di)^q ( mod di)
=(-1)^q*(n-q*di)!*q!*di^q ( mod di)
以下是对第二步的分析
((di-1)! mod di)^q:上面刚讲了
(n-q*di)!:因为N不一定是di的倍数,所以n-q*di相当于n%di(计算剩下的“尾巴”)(例如n=1000,di=13的时候,q=7,n-q*di=n%di=9,因此9就是这里的“尾巴”,这里(n-q*di)!就是9!)
q!*(di)^q ( mod di):窝也不会了咕咕咕


这是个Nim石子问题
我们先随便砍一刀

这么砍相当于把黑格子到上边的距离变短
同理,在哪边砍,就相当于把黑格子到哪边的距离变短
这就相当于有四堆石子的Nim石子游戏问题,石子数量分别是(x-1),(y-1),(n-x),(m-y)
于是就可以把这四个都异或起来,就可以判定先手是否必胜
但是题目问有几种
我们可以枚举啊

emmmmm
好大啊
长者说我国是数据结构强国,所以我们可以用数据结构(雾)
把式子变形

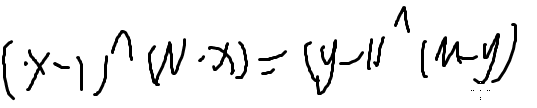
枚举所有的x,把左边算出来的数塞到数组里,然后就枚举y,看右边的结果在数组里出现了多少次
可以搞个桶排一般的数组,或者是排序后二分
安利网站codechef.com(CC)

分组不要求连续
哥德巴赫猜想?!


第二个已经被证明(证明见百度)
第一个在long long范围内是对的

一到n中所有数的和
s是偶数:输出2
s是奇数:N=2:s是质数:输出1
N≠2:看能拆成2个还是3个质数
拆成两个质数:这两个质数中一定有一个是2,所以看s-2是不是质数,如果是,输出2,不是,输出3

平面最远点对???(才没有辣么难)
先看看什么是曼哈顿距离

我们不知道是第一头牛的y大还是第二头牛的y大
于是就有了两种情况
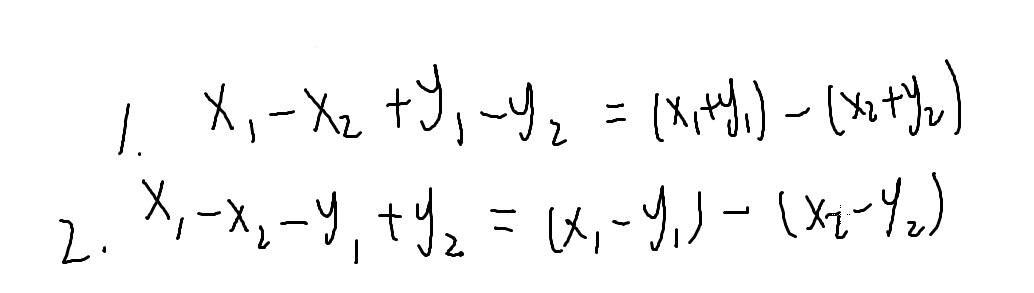
第一种情况是第一头牛的y大于第二头牛的y
第二种情况是第二头牛的y大于第一头牛的y
所以我们先按x+y排序,最大的减最小的,再按x-y排序,最大的减最小的

不考虑复杂度神马的,我们可以算出来从第一个城市到第二个城市有多少条边
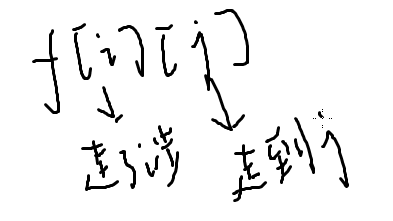
转移考虑从哪个点走过来
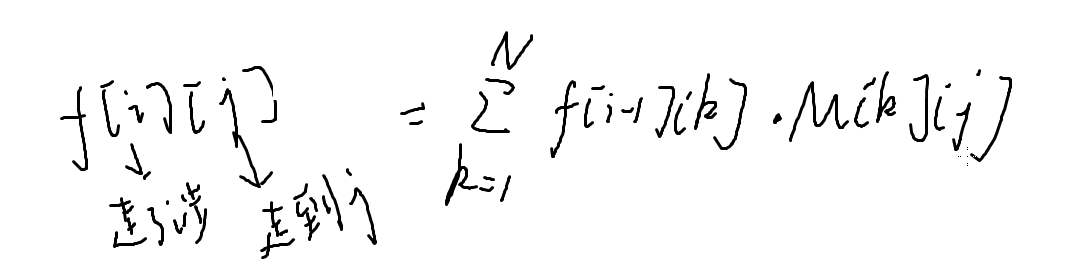
意思就是从起点走i步到j,中间一定会从起点走到k,再走一步到j,我们就枚举中间点k
复杂度:大概1024
能不能再快一点
如果把经过i条路到达的点的方案数看做一个矩阵
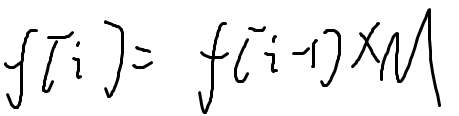
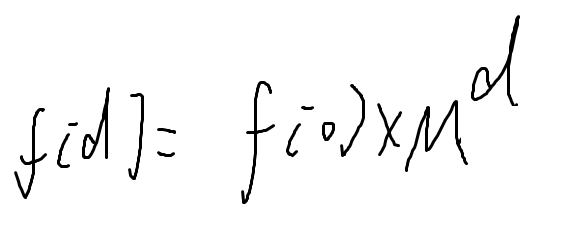
复杂度:O(n3logd)(大概1010)
还是慢了点
我们看题目中别扭的地方
算a到b的道路数目很鬼畜,而且复杂度还和k没有关系
那我们从k入手进行优化

我们在存的时候就换一下维度,然后发现这时矩阵乘法
M=out*in

但是现在还是要n3,还是过不了
我们暴力的把括号打开

矩阵有结合律,所以可以随便加括号
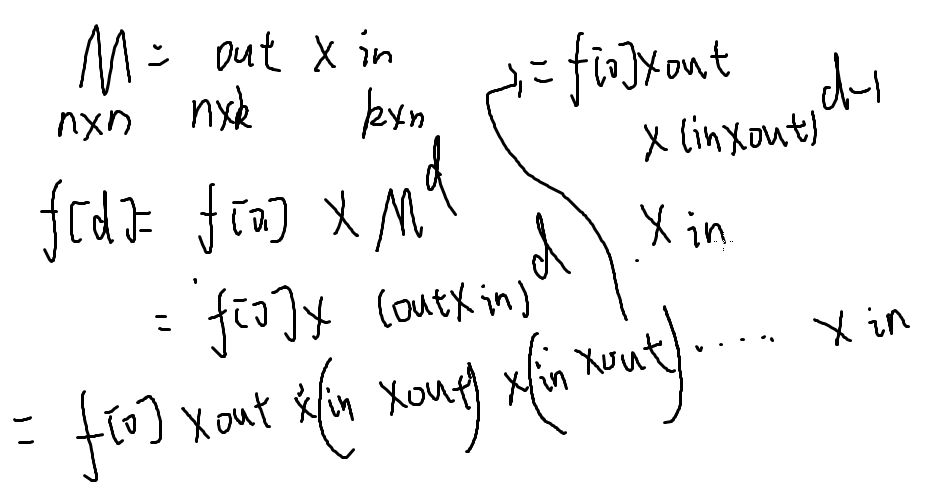
现在in*out就是k*k的矩阵
然后复杂度就变成了O(k3logd)
给一棵n个点的树,每个点有点权,保证点权在int范围内,有m次询问,每次给出两个点p1,p2,能否在p1到p2的路径上找出三个点,使得这三个点的点权能为一个三角形的三边长度
正难则反,我们想怎么不能构成三角形
如果出现这种情况就不能构成三角形了

当取等号的时候,就是斐波那契数列了
斐波那契数列是不能够组成三角形,而且每个点的点权尽可能小的情况
我们注意到题目里说了每个点的点权小于int ,那我们沿着斐波那契数列写下去,发现会有f43(大概是这个数)爆int,那下一个路径上的点权一定是在int以内,此时一定可以组成三角形,因此如果路径上点的数量超过42,就一定能够构成三角形。
否则呢?暴力呗。
找路径:当然是倍增求LCA辣
求个毛啊一步一步跳就好了反正不超过42步还好写





