7.18考试
T1


求个gcd就完事了辣
开long long:100pts
不开long long:80pts
开了long long的代码
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #define ll long long using namespace std; inline ll read() { char ch=getchar(); ll x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } ll a,b; ll gcd(int a,int b) { if(b==0)return a; return gcd(b,a%b); } int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); a=read();b=read(); ll c=gcd(a,b); ll d=(ll)(a*b)/c; ll ans=c^d; printf("%lld",ans); }
名言警句:十年OI一场空, 不开long long见祖宗
T2:



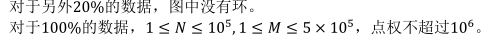
tarjan缩点+拓扑排序+dp
但是好麻烦啊,虽然长者说难度不是单调递增的,但也没说会递减啊(其实是不严格上升的)
T2不会辣么bt的辣
我们只需要找出从最小点到最大点或者最大点到最小点的路径就好了
长者说暴力可以拿省一,所以我们考虑暴力
最暴力的思路当然是枚举每一个点辣
我们直接枚举当前的max是哪个点,找出经过它的路径上的最小的点,然后做差
在走的过程中可能会出现某个点的权值比枚举的点大,但是木有瓜系,当我们枚举到那个更大的点的时候,答案就会覆盖住当前点。
那我们考虑怎么求出路径上最小值的点
跑一遍bfs就好了
但注意这里是有向图,所以可能是从当前这个点走到这条路径上的min,也有可能是当前路径上的min走到当前的点
举个栗子:
情况1:
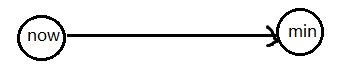
情况2:
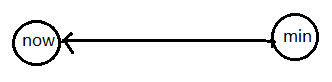
所以还要再往回bfs一遍
啥?为什么不是dfs?因为bfs能把所有到的点找出来,dfs就撞进南墙不复返了,就很容易漏掉情况(bfs60pts,dfs40pts)
这样会TLE几个点
标程优化:
我们发现时间都浪费在没有用的bfs上了
可以发现先枚举哪个点对最终答案没有什么影响,所以我们排序(从小到大)
举个栗子:我们先枚举点权最小的点(图中点的编号就是排完序后点的下标)

我们先枚举点1,发现自己就是最小的点,并且所有经过点1的路径中,点权最小值就是点1的权值(在这张图里面,点1,2,3,4的路径上最小的点权都是点1的点权)
再枚举点2,发现点2有一条路径经过了点1,那经过2的路径上,最小的点权就是1的权值
我们发现从min这个点出发,能够到达的点都不需要再枚举更新最小值(因为更新不更新都一个样子)
这样我们就记录已经算出答案的点,当bfs到已经算出答案的点时,就是已经算出答案的点的答案,然后return
蒟蒻还没有写代码,先上std
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> #include<queue> using namespace std; const int maxn=100010; const int maxm=500010; int n,m,en,result[maxn],z[maxn],y[maxn]; struct edge { int s,e; bool rev; edge *next; }*v[maxn],ed[maxm<<1];//因为牵扯到排序balabala,所以用指针 void add_edge(int s,int e) { en++; ed[en].next=v[s];v[s]=ed+en;v[s]->e=e;v[s]->rev=false; en++; ed[en].next=v[e];v[e]=ed+en;v[e]->e=s;v[s]->rev=true; } bool cmp(int a,int b) { return z[a]<z[b]; } void bfs(int p) { queue<int> q; if (!result[p]) result[p]=z[p]; q.push(p); while (q.size()) { int now=q.front(); q.pop(); for (edge *e=v[now];e;e=e->next)//相当于数组前向星的for(int e=head[now];e;e=edge[e].nxt) if (!e->rev && !result[e->e])//如果当前边的终点没有被遍历到过,就进行入队,更新 { result[e->e]=z[p]; q.push(e->e); } } q.push(p); while (q.size())//正着搞完反着搞 { int now=q.front(); q.pop(); for (edge *e=v[now];e;e=e->next) if (e->rev && !result[e->e]) { result[e->e]=z[p]; q.push(e->e); } } } int main() { scanf("%d%d",&n,&m); for (int a=1;a<=n;a++) scanf("%d",&z[a]); for (int a=1;a<=m;a++) { int s,e; scanf("%d%d",&s,&e); add_edge(s,e); } for (int a=1;a<=n;a++)//排序略迷??? y[a]=a; sort(y+1,y+n+1,cmp); for (int a=1;a<=n;a++) bfs(y[a]); int ans=0; for (int a=1;a<=n;a++) ans=max(ans,z[a]-result[a]); //result[i]记录经过i的路径上最小的点权 printf("%d\n",ans); return 0; }
T3



看起来是个状压dp(大法师)
f[s]代表s所对应的的这些人之间能不能通过交换变的合法
(emmm状态都设错了,然后就爆0了qaq)
怎么判断?
排个序,看c1,c2,能不能够成两把刷子,c3,c4能不能组成两把刷子...
但好像和这个题没有什么关系
n个人最坏情况下需要n-1次交换
why?
假设我们有一堆排好序的刷子,它们的属性值是c1,c2,c3,c4......

下面的编号是拿着这两把刷子的让你
情况1:拿着1本来就拿着c2,不用管
情况2:1还拿着魑魅魍魉,要和拿着c2的人交换1次
所以一次交换至少搞定一个人,最后一次交换一定可以搞定倒数第二个人和最后那个人
答案小于n-1:出现情况1
现在,f[s]表示s状态的这些人能不能内部消化,g[s]表示这些人合法需要的最小交换次数
s位上有k个1,则g[s]初始化为k-1,然后找比k-1更小的数
我们再看数据范围,N≤16,复杂度应该是O(3n)
这告诉我们要去枚举子集
枚举的子集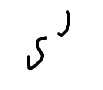
剩下的部分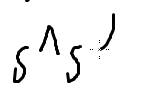
如果分成两部分:

(n/2-1)*2=n/2-2
我们发现每把s分出去一部分(这部分可以内部消化),g[s]就会减1
然后问题就变成了最多把多少人分成几部分,让他们自己换刷子解决问题
ans=n-部分的数量
那我们现在g[s]表示s最多能分成多少个合法的子集
g[s]=枚举子集s',看s'能分成多少个部分,s^s'最多能分多少部分,取max
也就是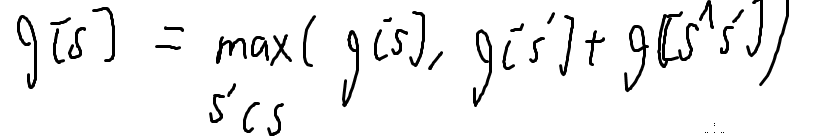
stdのcode
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int maxn=20; int n,d,z[maxn][2],y[maxn<<1],f[1<<maxn]; int main() { scanf("%d%d",&n,&d); for (int a=1;a<=n;a++) scanf("%d%d",&z[a][0],&z[a][1]); for (int a=0;a<(1<<n);a++) { int cnt=0; for (int b=1;b<=n;b++) if (a&(1<<(b-1))) { y[++cnt]=z[b][0]; y[++cnt]=z[b][1]; } sort(y+1,y+cnt+1);//按照刷子的属性排序 bool able=true; for (int b=1;b<=cnt;b+=2) if (y[b+1]-y[b]>d) able=false;//如果有一组不行 if (able) f[a]=1; else f[a]=-0x3f3f3f3f; } f[0]=0; for (int a=1;a<(1<<n);a++) for (int b=a;b;b=(b-1)&a) f[a]=max(f[a],f[a^b]+f[b]);//比较枚举的子集和剩下的部分,取最大的,就是最多能分出多少 if (f[(1<<n)-1]<0) printf("-1\n");//不是个正常的步数 else printf("%d\n",n-f[(1<<n)-1]); return 0; }
T4



这看起来是个线段树
但是给区间加上斐波那契数列怎么打标记啊!!!
不会,朴素暴力qwq
可爱的性质:
两个斐波那契数列的和是个伪斐波那契数列
先加一个a数列,再加一个b数列

相当于加上一个c数列
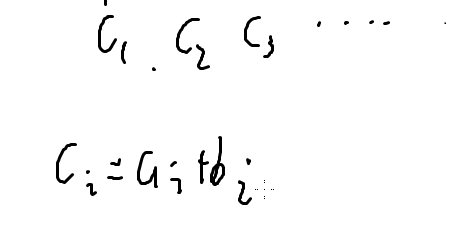
我们发现cn=cn-1+cn-2
所以我们打标记的时候就只需要记录c1,c2就好了,其他的就可以推出来了
那么给这段区间第一个数加上c1,第二个数加上c2,区间和会怎么变?
其实这只和c1,c2,区间长度有关
后面的ci都可以表示成kc1+qc2的形式
例如:

可以处理一个数组,f[i]第i项是多少倍的c1+多少倍的c2
求一个前缀和:对前i个数求前缀和,就是一段长为i的区间总累加的k1,k2
例如对c1,c2,c3,c4求前缀和
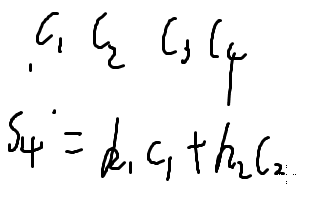
式子:

这样就可以算出来区间的和了
stdのcode
#include<cstdio> #include<cstdlib> #include<cstring> #include<cctype> using namespace std; const int BUF_SIZE = 30; char buf[BUF_SIZE], *buf_s = buf, *buf_t = buf + 1; #define PTR_NEXT() \ { \ buf_s ++; \ if (buf_s == buf_t) \ { \ buf_s = buf; \ buf_t = buf + fread(buf, 1, BUF_SIZE, stdin); \ } \ } #define readint(_n_) \ { \ while (*buf_s != '-' && !isdigit(*buf_s)) \ PTR_NEXT(); \ bool register _nega_ = false; \ if (*buf_s == '-') \ { \ _nega_ = true; \ PTR_NEXT(); \ } \ int register _x_ = 0; \ while (isdigit(*buf_s)) \ { \ _x_ = _x_ * 10 + *buf_s - '0'; \ PTR_NEXT(); \ } \ if (_nega_) \ _x_ = -_x_; \ (_n_) = (_x_); \ } //上面是个快读 #define wmt 1,n,1 #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 const int maxn=100010; const int mo=1000000007; int n,m,z[maxn<<2|1],col[maxn<<2|1][2]; struct rec { int a,b; rec(){} rec(int a_,int b_){ a=a_;if (a>=mo) a-=mo;//一开始就取模 b=b_;if (b>=mo) b-=mo; } }f[maxn],sum[maxn]; rec operator+(const rec &a,const rec &b)//结构体加 { return rec(a.a+b.a,a.b+b.b); } int operator*(const rec &a,const rec &b)//方便后面乘f数组 { return (1ll*a.a*b.a+1ll*a.b*b.b)%mo; } void update(int rt) { z[rt]=z[rt<<1]+z[rt<<1|1]; if (z[rt]>=mo) z[rt]-=mo; } void color(int l,int r,int rt,int a,int b) { col[rt][0]+=a;if (col[rt][0]>=mo) col[rt][0]-=mo;//col[rt][0]代表a1的标记 col[rt][1]+=b;if (col[rt][1]>=mo) col[rt][1]-=mo;//col[rt][1]代表a2的标记 z[rt]+= rec(a,b)*sum[r-l];if (z[rt]>=mo) z[rt]-=mo;//修改区间和 } void push_col(int l,int r,int rt) { if (col[rt][0] || col[rt][1])//如果有一个不为0,就要下放 { int m=(l+r)>>1; color(l,m,rt<<1,col[rt][0],col[rt][1]); int a=rec(col[rt][0],col[rt][1])*f[m+1-l];//因为这里对应a1,且a1是第一项,所以是乘f[m+1-l] int b=rec(col[rt][0],col[rt][1])*f[m+2-l]; color(m+1,r,rt<<1|1,a,b); col[rt][0]=0;//清空标记 col[rt][1]=0; } } void build(int l,int r,int rt) { if (l==r) { readint(z[rt]); return; } int m=(l+r)>>1; build(lson); build(rson); update(rt); } void modify(int l,int r,int rt,int nowl,int nowr,int a,int b) { if (nowl<=l && r<=nowr) { int a_=rec(a,b)*f[l-nowl];//这一个节点的a1的值累加起来 int b_=rec(a,b)*f[l+1-nowl];//这一个节点的a2的值累加起来 color(l,r,rt,a_,b_);//修改区间和 return; } push_col(l,r,rt); int m=(l+r)>>1; if (nowl<=m) modify(lson,nowl,nowr,a,b); if (m<nowr) modify(rson,nowl,nowr,a,b); update(rt); } int query(int l,int r,int rt,int nowl,int nowr) { if (nowl<=l && r<=nowr) return z[rt]; push_col(l,r,rt); int m=(l+r)>>1; int ans=0; if (nowl<=m) ans=query(lson,nowl,nowr); if (m<nowr) ans+=query(rson,nowl,nowr); if (ans>=mo) ans-=mo; return ans; } int main() { f[0]=rec(1,0); f[1]=rec(0,1); for (int a=2;a<maxn;a++) f[a] = f[a-1]+f[a-2];//预处理c1,c2的系数 sum[0]=f[0];//sum是前缀和 for (int a=1;a<maxn;a++) sum[a]=sum[a-1]+f[a]; readint(n); readint(m); build(wmt); for (int a=1;a<=m;a++) { int opt,l,r; readint(opt); readint(l); readint(r); if (opt==1) printf("%d\n",query(wmt,l,r)); else { int x; readint(x); modify(wmt,l,r,f[x].b,f[x+1].b); } } return 0; }





