7.18
博弈论dp
还是合并石子那道题,我们现在可以合并任意两堆,但是合并两堆的代价是它们的异或和,求合并成一堆的最小代价
N≤16
看起来像个状压dp
f[s]表示合并s状态的石子用的最小代价
s可以由s的子集推过来
判断子集:s&a=a,或者s|a=s,则a为s子集
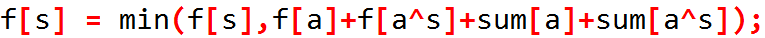
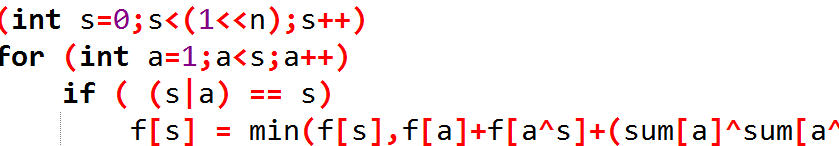
复杂度:O(4n)
我们发现他过不了,太慢了
那怎么优化?
我们发现第二层的循环枚举了很多不是s的子集的情况
所以我们直接只枚举s的子集

为什么这么写???
举个栗子:当前的s是1 0 1 0 1(代表4,2,0)
那么s-1=1 0 1 0 0,(s-1)^&s=1 0 1 0 0(代表4,2)
s-1-1:1 0 0 1 1 ,和s进行&操作后:1 0 0 0 1(代表4,0)
再减1:
优化之后就是O(3n)辣
博弈论dp正式开始
特征:
1.有一个游戏,玩家一定是A和B
2.是个回合制的游戏
3.这个游戏没有平局
4.胜负区分方法:当某个人无法进行操作的时候就输了
(fgo?战舰少女R?刀剑乱舞?)(算了算了非酋玩不了)(玄不救非氪不改命qwq)

把游戏状态抽象成一张图
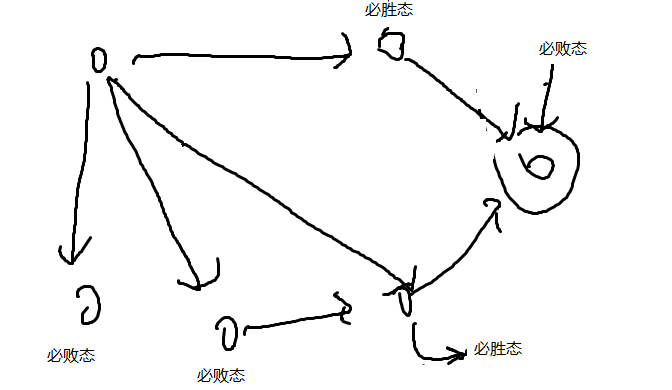
没有出边的点就代表无法进行下一步,所以是必败态。
能够走到必败态的点就是必胜态(因为必败态是对手操作)
那左上角的点呢?
这里就会有一个限制,A,B都绝顶聪明,会选择最优策略,所以左上角的点是必胜态
f[s]=true/flase表示是否是必胜态
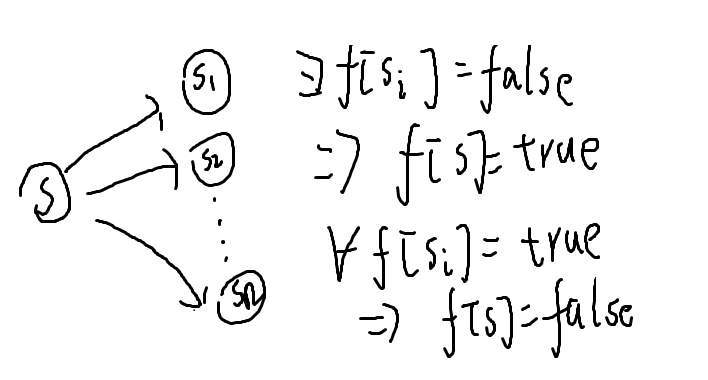
即它的转移状态中有一个是必败态,则它是必胜态,若所有都是必胜态,则它是必败态
回到这个题
f[i][j]表示s当前还剩下i,对手上一轮减了j,是必胜还是必败
转移:枚举r,1≤r≤j*k
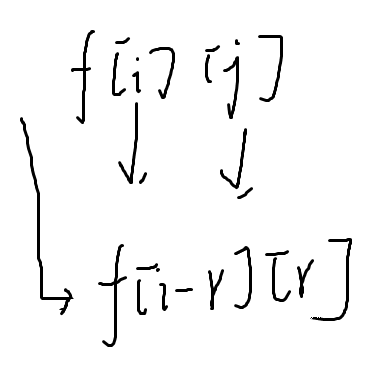
代码用记忆化搜索

第二类:
现在有两个强者A,B有N个游戏,同时玩
例如A可以在G1里面操作,B可以去G2里面操作
其他设定不变
输的条件是在每个游戏里面都无法移动
(立体五子棋?)(手动滑稽)
简单(雾)的例子:取石子游戏:
有n堆石子,第i堆石子的数量是ai,A先手,玩家可以从某一堆石子里面取走任意数量的石子(可以把这一堆取完),当没有办法取石子的时候就输了,也就是当一个人把石子变成0的时候,下一个操作的人会输
f[b1][b2]....[bn]:表示当前第i堆有bi个石子
转移:枚举从哪一堆石子中拿出多少个(貌似有点诡异)
这种方法除了炸了之外很完美
对于n个游戏,我们有SG函数
考虑只有一堆石子,先手必胜

0是必败态,所以sg[0]=0
找出i能转移到的所有状态,把这些状态的sg函数写出来,找出最小的没有出现的自然数,就是sg[i] //通顺emm
所以sg[1]=0.sg[2]=2(1可以转移到0,2可以转移到1,0)

我们发现这个题里的sg[i]=i
在这个题里我们可以手算出来所有的sg
举个栗子
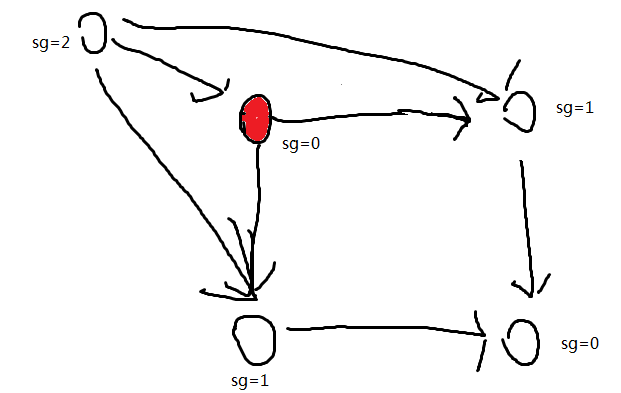
为什么红点的sg为0?
因为红点能够直接到达的点的sg是1,没有出现过的最小的自然数是0
sg=0,则先手必败
在这个题里面,ai的sg就是ai
那n个游戏的sg值怎么计算?
sg定理:n个游戏的sg值就是n个游戏的sg值异或起来
所以这里n个游戏的sg值就是a1^a2^a3^.............^an
如果sg值是0,先手必败
代码:

现在有N堆石子a1,a2,a3...an,可以从一堆石子里面取走1~4个石子,问先手必胜还是必败
sg[0]=0
sg[1]=1
sg[2]=2
sg[3]=3
sg[4]=4
sg[5]=0(因为5可以转移到4,3,2,1)
sg[6]=1(转移到5,4,3,2)
所以sg[ai]=ai%5
所以这个题就是(a1%5)^(a2%5)^.............^(an%5)
一般方法:手算sg值,找规律,把每个的sg值异或起来,看是否为0

这个题里面,石子堆和石子堆有关系了
一般思路:把问题转化为取石子1.0的形式
把所有石子数是奇数的堆的下标取出来进行异或,看是否为0
为什么?
每次操作的两堆只有下面两种情况:
(下面用1表示奇数的堆,0表示偶数的堆)
i j i j
1. 0 1 ------------------------------>1 0
2.1 1------------------------------->0 0
我们把红色的0看做是两个1,那么我们的操作就是一直把右边的1往左移
我们就把石子堆的值看成石子堆的数量,下标看成值,然后就转换成了1.0版本

把所有下标为奇数的石子数量异或起来
why?如果能把偶数位置搬到奇数位置,那就一定能把奇数位置搬到偶数位置,那偶数位置的石子好像没有什么用
所以就把下标为奇数的石子异或起来

每个格子到右下角的曼哈顿距离是不变的,如果我们能把偶数距离的石头移动到奇数距离的格子,那一定能从奇数距离的格子移动到偶数距离的格子,所以这个题和上题是一样的,只需要把奇数距离格子里的数异或起来就行了

显然这是只有一个游戏的问题
状压f[i]表示I状态的格子被标记了?
22000存不下qwq
所以我们考虑把它拆成多个游戏

我们发现在中间染色之后,左边两个格,右边两个格都不能染色了
sg[i]表示长度为I的横条的sg值
在上面这个条里面,答案就是sg[3]^sg[4]
代码求sg值

f[x][y]-------->f[1][x+y]
---------->f[2x][y]
----------->f[3x][y]
如果y>=n就是必败态,看谁能走到必败态,谁就是必胜态
N是30000,开个30000*30000的二维数组,几个G就存下了对吧qwq
好吧我们来谈正经的优化
我们发现第一维不可能取到不是2的倍数或不是3的倍数的数
所以f[a][b][y]表示现在是2a*3b是当前的x,




