7.17
dms去储备营了嘤嘤嘤
不过今天是zhx讲课qwq
DP
先看个例子
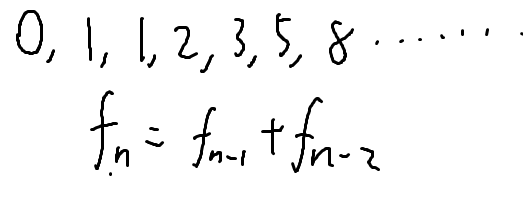
斐波那契数列对不对?
下面这个式子就是在告诉我们应该怎么算第n项
这个式子也就是其他算好的结果算自己的结果,是第一种写法
第二种写法:
用自己的结果算其他的结果
在这里,由fn可以推出fn+1,fn+2
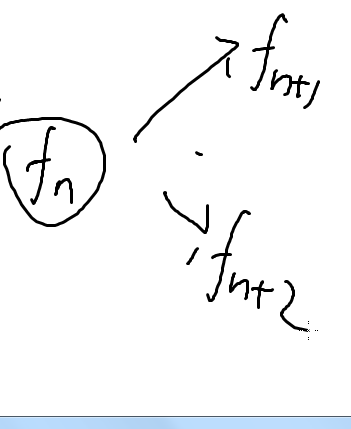
就像这样

注意有的题用一种方法难写,但用另一种方法会好写
最后一种写法
记忆化
先来个直白的搜索

复杂度:O(f(n))
因为f(n)是几,就需要几次return 1(或是return 0)
f(n)和2n是一个级别的
那为什么它出奇的慢?
因为它会重复计算很多次同一个项
那怎么办?
我们可以把搜索到的值记录下来
就像这个样子(传说中的记忆化搜索)
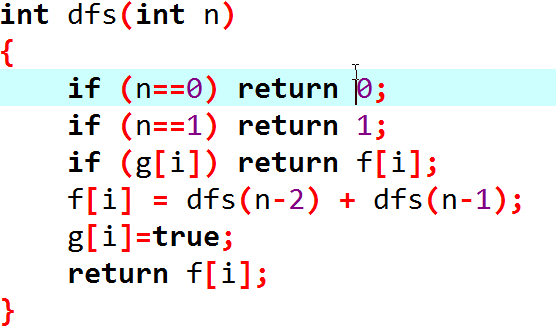
有些名词:
无后效性
阶段性
转移方程
状态
状态就是你要算什么,转移方程就是你怎么算
无后效性:状态视作点,转移视作边,这就是有向无环图
据说有乱序转移的题。这时转移关系是有向无环图,具有拓扑序。拓扑排序后for一遍就好了辣
特殊类型动态规划
数位dp
树形dp
状压dp
博弈论dp(明天讲)
背包
背包

f[i][j]表示前i个物品占用j的体积,最大价值是多少
i代表前i个物品已经考虑完了
当前物品只有放与不放两种情况
不放:f[i][j]=f[i-1][j]
放:f[i][j]=f[i-1][j-v[i]]+w[i]
为了最大化,所以我们取max
上面是别人更新自己的写法
自己更新别人的写法
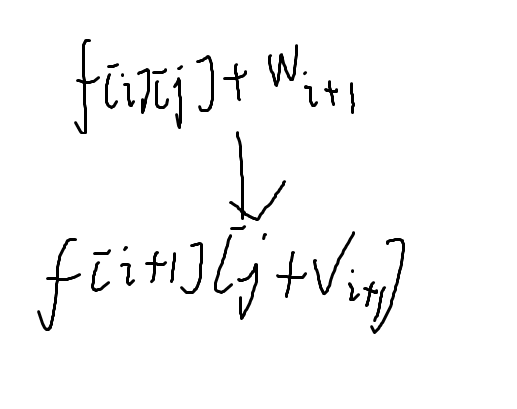
答案:max{f[n][j]}(0<=j<=m)
唉唉一维优化呢?
大概被吃了叭

 (第i个物品放0个的转移)
(第i个物品放0个的转移)
放n个:f[i-1][j-n*v[i]]->f[i][j]
所以我们枚举第i个物品放了多少个
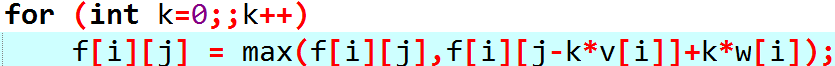
最内层循环
终止条件:k*v[i]>j
唉唉一维优化呢?都说了被吃了辣
我们发现它出奇的慢,因为这是三重循环
我们让他跑的快一点,变到n2级别
for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { f[i][j]=f[i-1][j]; if(v[i]<=j) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]); } }
为什么这样改就是对的?
我们之前说过dp是一个DAG
我们不妨来画个图
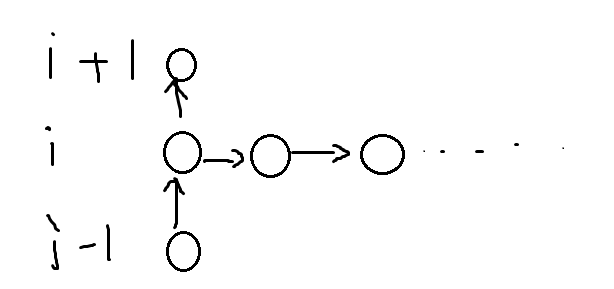
因为物品可以选无限个,所以递推的时候就可以向上走,也可以横着走,这样横着走就是f[i][j-v[i]]

1.枚举第i个物品用多少次O(nm每个物品个数)
2.考虑优化
我们可以把几个物品捆绑一下
比如这个物品有13个,我们就把它捆绑成酱紫
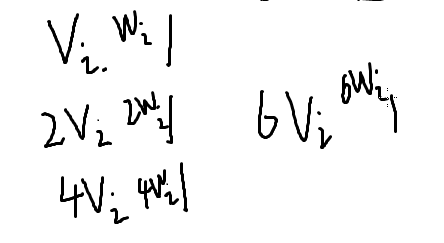
我们这么捆绑,那么无论用这个物品选几个,都可以用这些捆绑后包的组合来表示
每个捆绑包只能用一次,所以就变成了01背包
复杂度O(n2k) k是捆绑包的个数
不难猜出捆绑包是按二进制拆的
但最后一个为什么是6不是8?
13-1-2-4=6,6<8,所以是6
就是当最后的数(原数-20-21-22....)不够2k时,最后一个捆绑包的大小是最后的数
造捆绑包:

完整版代码
int main() { cin >> n >> m; int cnt = 0; for (int a=1;a<=n;a++) { int v_,w_,z; cin >> v_>> w_ >> z; int x = 1; while (x <= z)//制造捆绑包 { cnt ++; v[cnt] = v_*x;//注意捆绑包的权值和体积都跟着变 w[cnt] = w_*x; z-=x; x*=2; } if (z>0) { cnt ++; v[cnt] = v_*z; w[cnt] = w_*z; } } n=cnt; for (int i=1;i<=n;i++) for (int j=0;j<=m;j++)//对捆绑包进行01背包的操作 { f[i][j] = f[i-1][j]; if (j >= v[i]) f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]); } int ans=0; for (int a=0;a<=m;a++) ans = max(ans,f[n][a]); cout << ans << endl; return 0; }
基础类dp
ioi真题之-----------------------
数字三角形
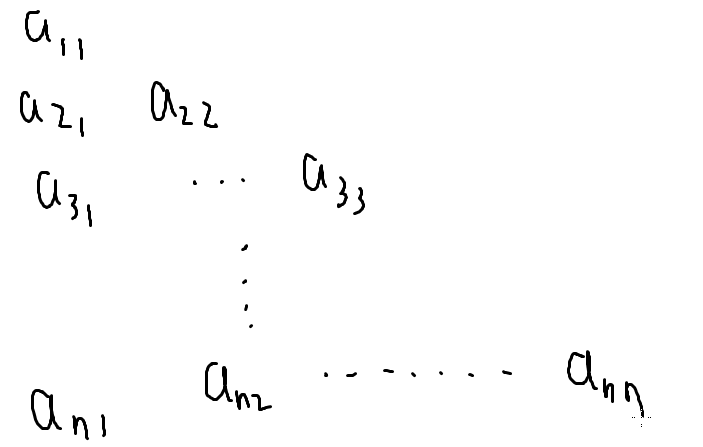
咋做?
当然是用dp辽
状态:f[i][j]表示在a[i][j]时的最大值
转移方程
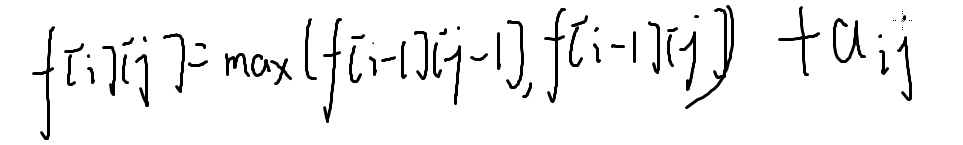
数字三角形2
求mod100之后的和最大
记录f[i][j]mod 100的最大值?
错
why?
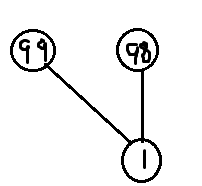
如果选f[i-1][j-1],f[i-1][j]中的最大值来进行转移
那对于a[i][j]=1的这个点来说,f[i][j]=0,因为我们选择了点权为99的那个点来更新它
但其实选择98的那个点更优
经典套路:目前做不出来,加维度。加一维不够,再来一维。
定义f[i][j][k]是走到(i,j)时,当前的和mod 100==k是否可行
有两种情况
f[i][j][k]=true:更新
f[i][j][k]=false:什么也不做
更新:
向下走:
f[i+1][j][(a[i+1][j]+k])%100]=true
向右走:
f[i+1][j+1][(a[i+1][j+1]+k)%100]=true
最后答案:最后一行f值为1的最大的k
最长上升子序列
f[i]表示以i结尾的最长上升子序列的长度
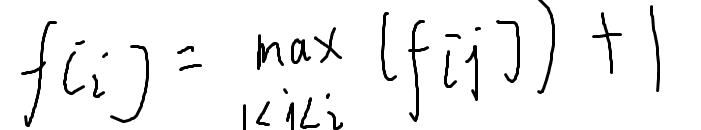
复杂度O(n2),显然太慢了,所以我们要进行一番优化
我们要的是j<i的最大值,所以我们可以搞个线段树什么的
所以我们有些时候可以用数据结构优化dp求值
常用技巧:加维度,数据结构(多一个条件,多一个维度)
区间dp
有好多堆石子排成一排,每次可以选择合并相邻两堆,代价就是合并的这两堆的石子个数,求最终合并成一堆最小代价
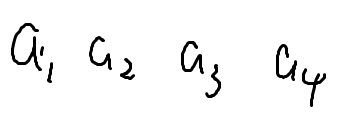
满足合并相邻的两个东西,就是区间dp。
我们发现如果我们合并了a1,a4,则a2,a3都在这一堆石子里面
f[l][r]:第l堆石子到第r堆石子合并起来的最小代价
初始化:f[i][i]=0
我们要合并l到r,首先要合并l到k,k到r(l<=k<r),这个k就相当于分界线一般的存在。
所以我们枚举分界线
f[l][r]=min{f[l][k]+f[k+1][r]}+a[l]+a[l+1]+a[l+2]....+a[r]
后面这些a[i]是[l,r]的区间和,区间和用前缀和来求
也就是f[l][r]=min{f[l][k]+f[k+1][r]}+sum[r]-sum[l-1]
典型错误示范:
for(int l=1;l<=n;l++) for(int r=1;r<=n;r++) for(int k=l;k<r;k++) f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+sum[r]-sum[l-1]);
为什么是错的?
这样我们是先算左端点为1的区间,再算左端点为2的区间....
但是当我们算到f[1][n]的时候,假如p枚举到3,但是f[4][n]没有算出来
正确示范:
for(int len=2;len<=n;len++) for(int l=1,r=len;r<=n;l++,r++) for(int k=l;k<r;k++) f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+sum[r]-sum[l-1]);
这里规定了区间长度,是按照区间长度从小到大的,也就保证了上述例子中的f[4][n]会在f[1][n]之前算出来
我也不造这到题叫啥
我们有N个矩阵,告诉你每个矩阵的大小,数据保证它们可以乘起来
就像酱紫
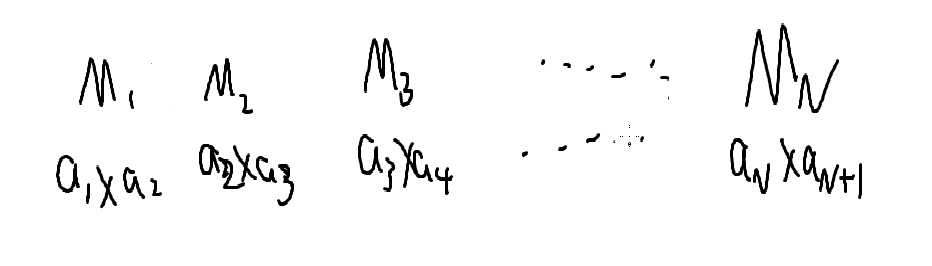
问把这些矩阵乘起来的最小次数
举个栗子
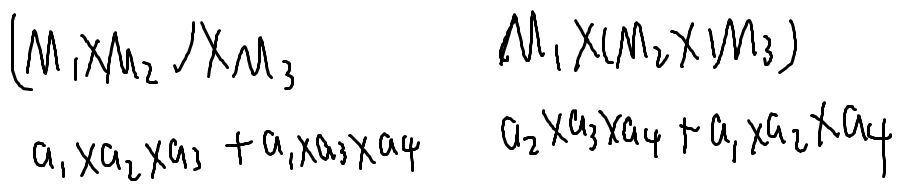
f[l][r]表示把第l个矩阵到第r个矩阵乘到一起,所花费的最小次数
则f[l][r]=min{f[l][k]+f[k+1][r]+al*ak*ar}(l<=k<l)
为什么?
我们结合上面给出的例子,发现多增加的步数就是第一个矩阵的行*第一个矩阵的列*第二个矩阵的列
状压dp
在二维平面上有n个点,坐标为(xi,yi),问求从1号点出发,把所有的点都走至少一遍之后再回到1号点,最短的距离是多少(想怎么走怎么走)
就比如这两个点之间可以这么走

当然我们知道两点之间线段最短
每个点没有必要走两次
dp设计要考虑变化量有哪些
这里的变化量就是我们当前在哪个点,已经走过哪些点

但是走过了哪些点不能直接用一个整数表示,而是要用数组表示
这时候就是状态压缩了(把这个数组压成一个数)
每个点只有走过和没走过两种状态,所以用0表示走过,用1代表走过
假设我们现在到过1,2,4折三个点
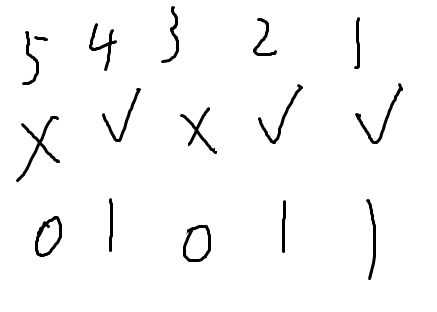
这就是一个二进制数
所以f[s][i]中的s就是状态压缩后的数
在转移的时候要考虑哪个位置没有到达过,也就是s的二进制表示中哪一位是0
判断哪一位是0:(1<<i)&s==0,则第i位是0(注意这里是按照2k的第k位,即存在第0位)
最终答案:min{f[(1<<n)-1][i]+juli(i,1)}
juli就是计算两点间的距离
复杂度O(2n*n2)
数据范围:n≤22或n≤20

f[i][s]表示前i行草种完,第i行的草长的样子
(s的二进制表示每个位置有没有种草)
如果两行之间有相邻的草,则s&s'不为0
判断草不相邻:(j&(j<<1))=0&&(j&(j>>1))==0
判断贫瘠的地方不种草:将每行能种草的地方压成一个二进制数no[i],然后j&no[i]=j,就说明贫瘠的地方没有种草
先枚举这一行的种草情况j,再枚举上一行合法的种草情况k,k&j==0即为合法情况
代码:
#include<bits/stdc++.h> #define ll long long using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } int n,m,f[20][1<<12+9],ans; const int mod=100000000; int no[20],mmax; int main() { m=read();n=read(); for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) { int x=read(); no[i]+=x<<j-1;//no[i]代表第i行能种草的情况 } } mmax=(1<<n)-1;//所有格子都种草的情况(也就是最大的情况) no[0]=mmax; f[0][0]=1; for(int i=1;i<=m;i++) { for(int j=0;j<=mmax;j++) { if((j&no[i])!=j)continue; if(((j<<1)&j)!=0||((j>>1)&j)!=0)continue; for(int k=0;k<=mmax;k++) { if((k&no[i-1])!=k)continue;//对枚举的k进行相同的操作 if(((k<<1)&k)!=0||((k>>1)&k)!=0)continue; if((k&j)==0) { f[i][j]+=f[i-1][k]; f[i][j]=(f[i][j]+mod)%mod; } } } } for(int i=0;i<=mmax;i++)//把最后一行加起来 ans=(ans+f[m][i])%mod,ans=(ans+mod)%mod; printf("%d",ans); }
luogu P1879

这里要求恰好k个国王,所以我们再加一个维度
f[i][s][j]表示前i行已经摆好,第i行摆了j个国王,长成s的样子
再注意一下对角线的判断
luogu P1896
数位dp
顾名思义,这是按照数的高位推导数的低位的dp
T1:给出两个数l,r,问l到r中有几个数
当然是r-l+1了
不过我们用数位dp做
我们还是要联系上面的r-l+1这个式子
要求r-l+1,我们一般用前缀和来实现,即sum[r]-sum[l-1],所以我们就把问题转化成了求0~x中的数的形式
先算0~r中所有的数,再算0~l-1中所有的数
这样就都是形如0~x的形式了
即求y,0≤y≤x
假设x是3245,那么y最多有4位
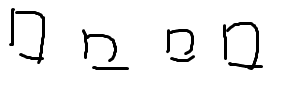
这样我们就转换成了填数问题
我们考虑到底是从高位开始填还是从低位开始填
如果我们从低位开始填
我们在个位填个9,能说明什么?
什么都说明不了
但我们从最高位开始填,如果填了9,就能说明当前数一定比x大,如果填了1,就说明当前数一定比x小
用f[i][0/1]表示填到第i位,当前的数已经填上的那几位是否与x的对应位相等
所以这里我们要先预处理x的每一位上的数
while (x>0) { l++; z[l] = x%10; x/=10; }
数位dp转移:
枚举下一位填0~9当中的哪个数
肯定会有填某些数不行的情况,那么哪些情况不行呢?
当j已经=1,且枚举的K大于x对应的位的时候,就不行了
当j=1且枚举的k与x对应位相等时,f[i-1][j]=f[i][j]
当j=0时:枚举的每一个k对答案的贡献是f[i][j],所以是f[i-1][j]+=f[i][j]
自己按照记忆胡的代码
while(x) { l++; z[l]=x%10; x/=10; } memset(f,0,sizeof(f)); f[l+1][1]=1; for(int i=l+1;i>1;i--)//这里是自己更新别的写法 { for (int j=0;j<=1;j++) { for (int k=0;k<=9;k++)//枚举这一位填什么 { if (j==1 && k>z[i-1]) continue;//如果不行,就continue int j_;//判断要更新的j if (j==0) j_=0; else if (k==z[i-1]) j_=1;//如果这一位填到了和x的对应为相等的数,且j=1,则j_也是1 else j_=0; f[i-1][j_] += f[i][j];//更新 } } }

什么意思呢?
假设[l,r]区间里的数是 19,20,21,那ans=1+9+2+0+2+1=15
设g[i][j]表示填到第i位,与x的关系是j的数位之和
枚举填的数k,计算对答案的贡献。
j=0:对答案的贡献是k*(f[i][j]) 这里的f[i][j]就是上一个题中的f[i][j](也就是数的数量)
递推式:
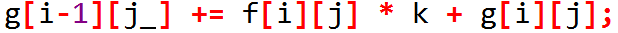
为什么要加g[i][j]?因为前面的f[i][j]*k是当前枚举的K对答案的贡献,是增加量,还要再加上原有的g[i][j]

加一维海阔天空
f[i][j][k]:i,j定义不变,k表示第i位填的k
枚举是只要避开两位之差小于2的情况

多一个条件,多一个维度
f[i][j][r],r代表已经填了的数字的乘积
枚举第i-1位填什么,r就直接乘
但是我们发现r炸了,r太大了,数组开不下啊
再来一维?
错,是再来好几维
我们发现r的因数里面不能有超过10的质数,所以数组有大部分是空的(就像我的脑子一样qwq?)
于是我们多来几个维度
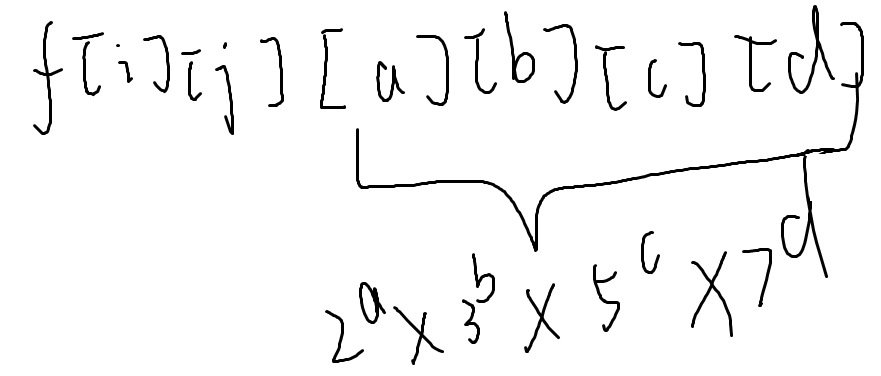
然后我们还是过不了qwq
继续优化ρωρ
下面是abcd的大概取值
a:60 b:30 c:20 d:10
我们发现abcd不可能同时取到上界,因此还有很大的浪费
对此强(sang)大(xin)无(bing)比(kuang)的官方是这么干的:
预处理所有可能取到的数,f[i][j][k]表示当前这个数是这些数中的第几个
树形dp
长者的简单题
给你一棵n个点的树,求这棵树有多少个点
n个点,此题完毕
并不
树形dp:dp子树的信息,从下往上来
放在这个题里面,f[i]表示以i为根的子树有多少个点
f[i]=∑f[j]+1(j为i的儿子)

神马是树的直径?在树上找到两个点,使得这两个点的距离最远
路径与子树有什么关系?
我们求两个点的路径,就要找lca
我们一般都是这么走的
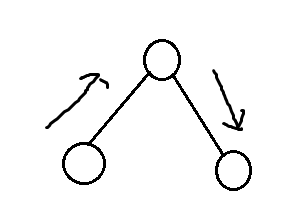
(最上面的点是lca)
现在我们这样走
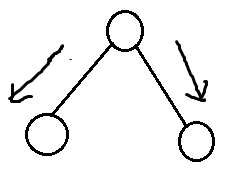
这样我们找最大值,就变成了找这个lca向下的最长的路径
最长的路径当然是向下最长路+向下次长路咯

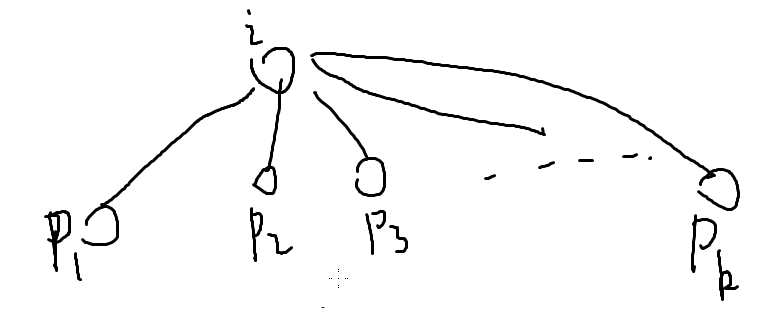
现在所有的pj的f都求出来了
我们要求最大值,那肯定是最大的那个f[p][0]+1咯
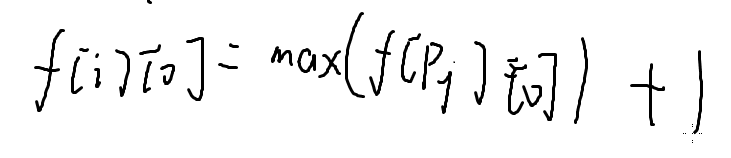
次长:
所有儿子的最长路和次长路混在一起求?
错
如果有一个pk,它很神仙,f[pk][0]是pk和它的所有兄弟中最长的那条边,f[pk][1]是次长的那条边
那么这样最长选了pk,这么找次长也可能是pk,这就不合法了
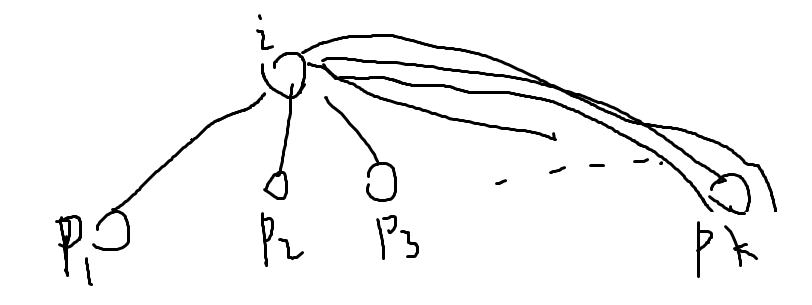
所以我们应该是在所有儿子的最长路中找最长。因为次长路不可能比所有的f[p][0]中次大的那个还长
伪代码(雾)

求树上所有路径的总长度之和
用f[i]表示以i为根的子树有多少个点
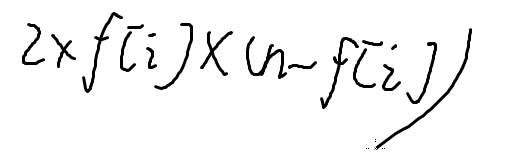
思想:看有多少条路劲经过当前枚举的这条边
一条边被算进路径:在子树里找一个点,在子树外面找一个点,这样一条路径肯定会经过这条边
因为可以正着走,也可以反着走,所以要*2

f[i][0]代表不选I的最大价值
f[i][1]代表选i的最大价值
选的时候,所有儿子都不能选
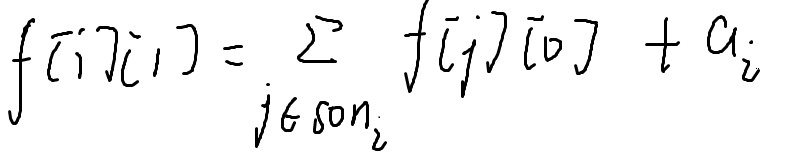
不选的时候,儿子可以选,也可以不选,取最大值
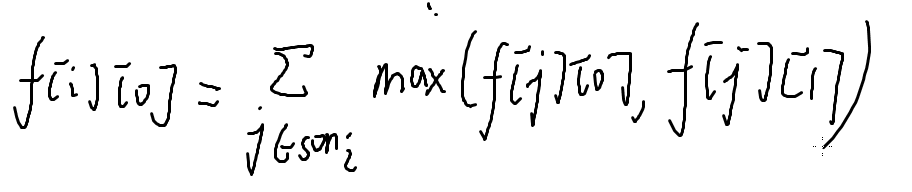

和上个题的思路差不多
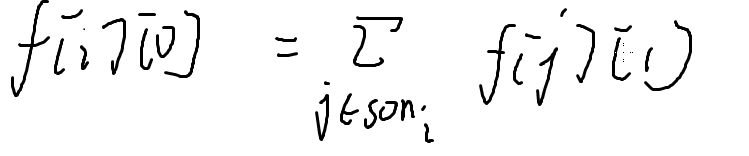
f[i][1]=∑min(f[j][1],f[j][0]) (后面没有+1)
拓展
每个士兵可以守护与自己距离不超过2的所有节点,求守护所有节点最少的士兵数量
加维警告
f[i][0/1/2]以i为根的子树被全部覆盖,i向下走,到达最近的士兵的距离
f[i][0]:在i上放士兵
这时候它的儿子放的士兵就与它无瓜了
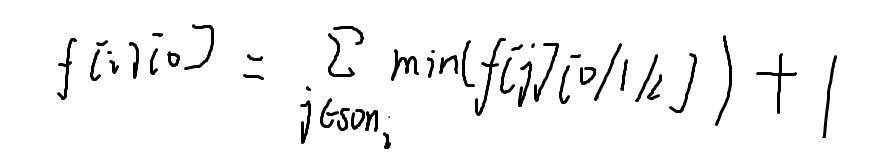
f[i][1]就有点让人![]() 疼了
疼了
这时候我们另外跑一个dp来算它
g[j][0/1]表示是否有一个儿子距离下面的士兵的距离是0(也就是第j个儿子有没有士兵)
f[i][2]
还是要跑个dp
dp套dp真的是涨姿势了




