7.14
一些安利(一些网站)


codeforce:炒鸡刺激的卡别人的那个网站
分治
分治,就是分而治之。
一般用途:纯二分,最值的最值(就是最大值最小这类的),以及昨天的毒瘤T3,二分答案加检查类型的鬼畜题目
借教室:

这是一道线段树板子题(雾)
其实这道题用二分
二分在第几份订单跪掉,然后检查就完事了
代码:
#include<bits/stdc++.h> #define ll long long using namespace std; ll read() { char ch=getchar(); ll x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } ll c[1000009],exc[1000009],n,m,a[1000009],d[1000009],s[1000009],t[1000009],ans; bool check(ll fen) { memset(exc,0,sizeof(exc)); for(ll i=1;i<=fen;i++) { exc[s[i]]+=d[i];//这里是反过来计算需求量 exc[t[i]+1]-=d[i]; } for(int i=1;i<=n;i++) { c[i]=c[i-1]+exc[i]; if(c[i]>a[i])return false; } return true; } int main() { n=read();m=read(); ll la=0; for(ll i=1;i<=n;i++) { a[i]=read(); } for(ll i=1;i<=m;i++) d[i]=read(),s[i]=read(),t[i]=read(); ll le=1,ri=n; while(le<=ri) { ll mid=(le+ri)>>1; if(check(mid)) le=mid+1; else { ans=mid; ri=mid-1; } } if(ans!=0) printf("-1\n%lld",ans); else printf("0"); return 0; }
三分
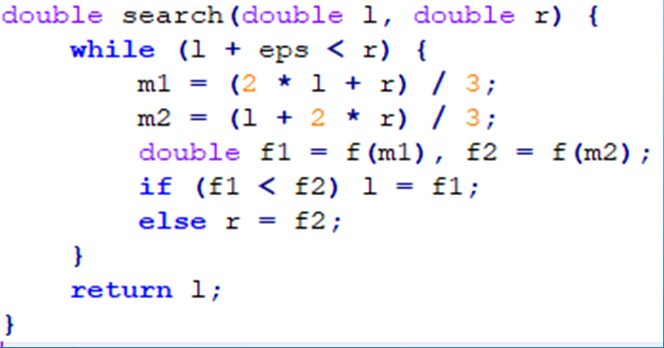
也可以用黄金分割率神马的,不过代码会很难看,还会精度丢失
如果一个函数长的特别骚,像这种

那就把它割成n段,由于求一个峰值是logn,所以我们可以把他切成100000段,然后在每一段的最大值中选最大的(当然还可以模拟退火什么的)

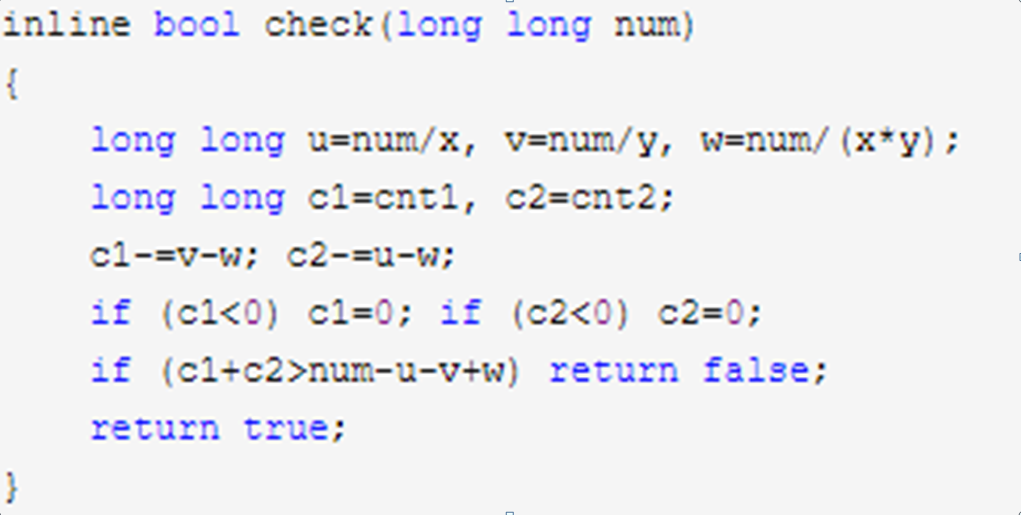
垃圾分类题

注意这里给了小A的数就不能给小B了
我们这里依旧是二分答案+check
我们发现被x整除或者被y整除的数可能有很多,这样就构成了很多垃圾数,于是我们可以像垃圾分类一样,对数进行分类
我们可以先找出来既被x整除,又被y整除的有害垃圾,把它们扔掉
然后我们看只被x整除的数能否扔给B,和只被y整除的数能否扔给A,如果都扔完了还不够cnta或者cntb,那当前检查的数肯定就不行。
否则就可以
分块
分块大概就是大块标记,小部分暴力(暴力到想不到)


我们有很多块
问题一:
区间l,r有那么几种情况
1.他们在同一个块里,暴力加(O(√n))
2.在相邻的块里,依旧暴力跑(O(2√n))
3.l,r隔得挺远:中间整块用tag,零碎部分暴力
问题2:
既然询问是查找比x大的数,那我们不妨先对每一块里的数进行排序,排完序后保证每个块内的数有序,但是全局不一定有序
假设我们一个块内有3个数
原序列:325 817 541
排完序:235 178 145
(每一块之间有空格)
情况还是问题1的三种情况,对于情况1,2,直接O(√n)暴力
对于情况3,中间的整块跑二分,零碎部分暴力。
区间加:整块打标记,零碎部分在原序列加,然后零碎部分所在的块重新排序(是不是暴力的不要不要的?但是复杂度只有√nlogn)
问题3:
这m个数都是整数,开根后向下取整、
我们发现打开跟标记根本没法打。那就暴力呗(反正分块本身就暴力的不要不要的)
我们发现0,1开根后向下取整都是自身。那么当一个数开根成0或1后,开根和不开根是一样的。所以我们对于开根命令每次都暴力开,当有一个块全部都是0和1的时候,他就成熟了,就会自己开根号了,就不用管它了。就算是longlong也只用开6次根号,所以时间复杂度是可以接受的


思路有点像选择客栈qwq
关于查询所有pre[i]<l,这个就是上面的问题二。所以现在我们已经切掉了查询
修改:对每个颜色维护一个set,把同种颜色丢进去,如果要修改,就把前驱,后继抠出来
搜索

1.dfs(大法师大法好)

好写好想,不好拿分
空间占的相对广搜来说要小一些(搜索树极深极窄除外)
但是不要试图让dfs来跑最优解,会T成狗的qwq
bfs

拿广搜走个迷宫玩个八数码啥的还是可以的,但赶不上双向bfs
bfs进化版:双向bfs

如何双向bfs?
我们现在有起点,终点和两个队列q1,q2
我们先让q1扩展一步,再让q2扩展一步,然后q1再扩展一步,这样交替扩展两个队列,当所有节点都被遍历过的时候就停止。最后看是否存在一个点被遍历了两遍。
它比广搜好在哪呢?
这是广搜的搜索树
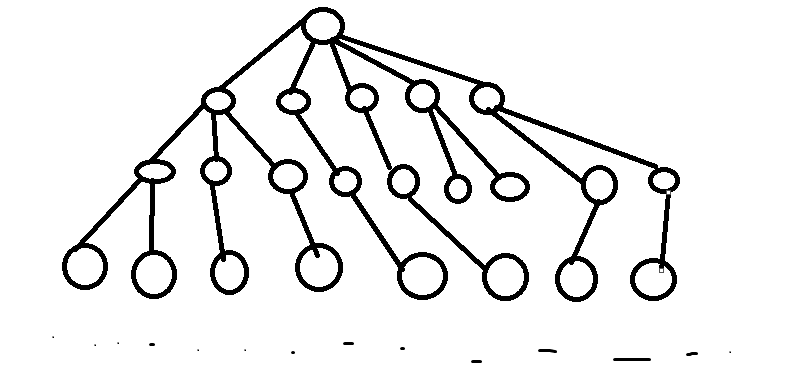
双向广搜:

从搜索树就能看出来了叭
数论


扫盲扫着扫着蒟蒻的我就瞎了
我们先来看看恶心的高精
高精加减乘都知道,那我们来看看没有人想敲的高精除高精
小学老师教过我们,用试除法,按照乘法口诀来试。但是计算机不会试除法,也没有乘法口诀,那咋办?用减法来模拟呗。
#define ll long long struct gaojing{ ll a[10009]; int size; }; gaojing operator / (gaojing a,gaojing b)//a是被除数,b是除数 { gaojing c; c.size=a.size-b.size+1; for(int i=a.size-1;i>=b.size;i--) { a.a[i]+=a.a[i+1]*10; a.a[i+1]=0; if(a.a[i]==0)continue;//位不够了 for(;;) { bool geq=true;//意思是大于等于b(当前截取的a的这几位) for(int j=i,k=b.size-1;k>=0;j--,k--) {if(a.a[j]>b.a[k]){geq=true;break;}//不相等的一位就可以判断大小了 if(a.a[j]<b.a[k]){geq=false;break;} }if(geq==false)break;//在上面的借位操作之后还是带不动,那就可以闪人了 c.a[i-b.size+1]++;//由于是开减法模拟,所以每次的增量是1 for(int j=i-b.size+1,k=0;k<b.size;j++,k++) //减法 { if(a.a[j]<b.a[k]) { a.a[j+1]--; a.a[j]+=10; } a.a[j]-=b.a[k]; } } } }
连高精除高精都可以打出来,那么还有什么不可以高精的???
接下来就是玄学的不要不要的高精度开方!!!!!

好了我们举个栗子
2.718281828(没错接下来我们要把e开方)
step1:以小数点为分界线,两个数一组,就像酱紫

step2:考虑每组内的最大完全平方数(把这一组的个数字当做两位数),然后像这样

step3:计算(1*20+x)*x最接近171的x,这里是6
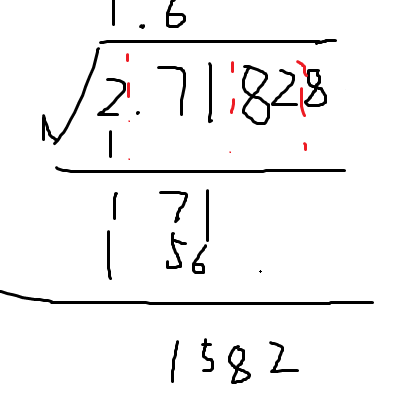 (这里因为158不够16*20,所以要写成1582
(这里因为158不够16*20,所以要写成1582
step4:再找(16*20+x)*x最接近1582的x
每次乘20的就是竖式上面的东西
为什么要乘20?
记住就好,没有为什么
代码什么的当然是咕咕咕了
麻麻再也不怕我不会开方了qwq
快速幂
快速幂当然都会咯,我们这里谈谈矩阵快速幂qwq
先来一发快速幂板子
ll ksm(ll a,ll b)//这里木有mod { ll r=1; while(b)//计算ab { if(b&1)r*=a; a*=a; b>>=1; } return r; }
再来看矩阵快速幂
其实只要重载矩阵的乘号就可以了
重载:
jz operator *(jz a,jz b) { jz c; for(int i=1;i<=n;i++)//n是a的行数 { for(int k=1;k<=m;k++)//m是b的列数 { for(int j=1;j<=r;j++)//r是b的行数 c[i][j]+=a[i][k]*b[k][j]; } }
矩阵快速幂有什么用呢?
对于一些恶心的递推的函数我们可以构造矩阵,然后使用矩阵快速幂优化(最骚能到O(dloglogd)))
高斯消元
行列式的值:削成上三角矩阵,对角线乘积
欧拉筛and欧拉函数
欧拉筛就是线性筛辣
欧拉函数φ:
n=p1q1+p2q2+p3q3+p4q4......
φ(n)=n(1-1/p1)(1-1/p2)(1-1/p3).....
φ的计算1:
按照公式老老实实算
φ的计算2:
素因子p第一次出现:phi*=(p-1),否则phi*=p
据说是计算1的展开
实现:代码咕咕咕
在欧拉筛时计算

因为欧拉筛时积性函数,所以在情况1下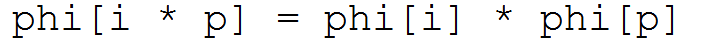
返回φ的定义,可知情况2的φ

推导
n=p1q1*p2q2*p3q3..........
φ(n)=n(1-1/p1).........
=n((p1-1)/p1)........
=p1q1*p2q2*...*(p1-1)/p1...........
=p1q1-1*p2q2-1..........
φ(i*p1)=p1q1*p2q2-1*p3q3-1........
=φ(i)*p1
莫比乌斯函数(一点点)

约数个数:(q1+1)(q2+1)(q3+1)....................(这里的q1,q2,q3的意义和上面的一样)
n/1+n/2+n/3+.....+n/n,每一项都向下取整,n=1014


why?
就算这个n很强大,当k<sqrt(n)时,每个k的取值都不同,也只有sqrt(n)种,k>sqrt(n)同理

我们可以搞个上面的循环,从i到j的整数t,n/t都是k
举个栗子
n=10,i=4
则k=2,j=5,
10/4=2,10/5=2
然后就做完了
代码
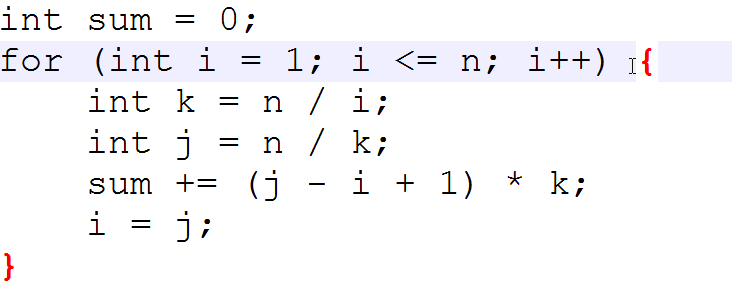
最大公约数
辗转相除太慢了(取模会拖慢速度),我们来个快速最大公约数(这个可以进行高精度最大公约数)

什么意思呢?
当x,y都是偶数的时候,那么它们的最大公约数就是2*gcd(x/2,y/2)
其中有一个是偶数,另一个是奇数,那么它们的最大公约数一定没有2,所以是偶数的那个除以2后,答案不变
如果都是奇数,就用更相减损术,减出个偶数来
玄学的A*
breath first search+best first search=A*
就是广搜和贪心搜索的结合体辣
为什么不直接用贪心搜索呢?
这是贪心搜索搞出来的
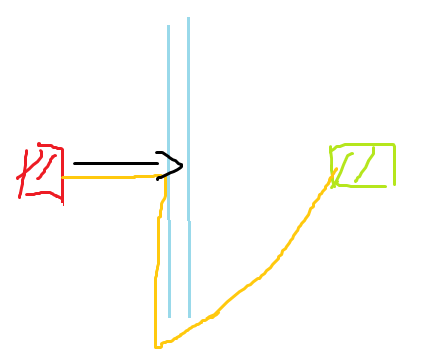
然而这才是最优解
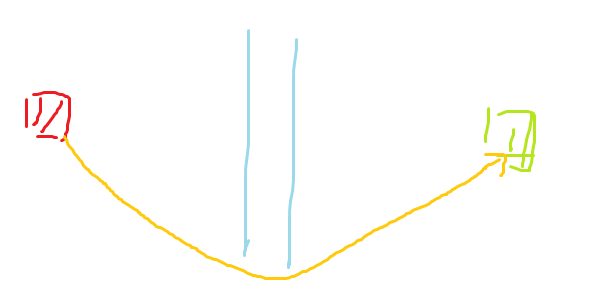
所以我们把这两个结合一下

通俗的说,g*(x)就是起点到当前点的最短距离,g(x)就是到这个点的实际距离,f(x)是不管障碍的情况下当前点到终点的最短距离(也就是估计),f*(x)就是处理障碍时的最优距离(也就是现实)(当然只有神仙才知道f*(x)是个什么东西)
g(x)和g*(x)的区别:
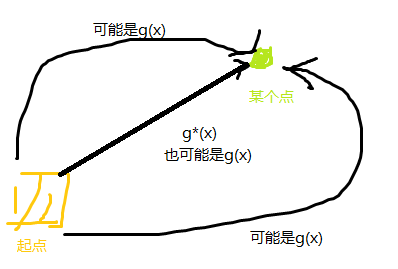
最后一个式子玄学证明:你的神仙预测肯定要比实际情况要小啊
其实只有当一直满足最后一个式子,最后等于的情况才是最优解
实现的思路:按照g(x)+f(x)排序,越小的节点越先扩展。
扩展着扩展着就找到了最优解qwq
A*就像一个有脑子的小朋友,bfs就像没脑子的小朋友,dfs在一边不断撞墙撞的很欢
题外话————排列编码

求rank
a[i]记录第i数字后面有几个数比当前的数小,∑a[i]*i!就是这个排列的rank
举个栗子
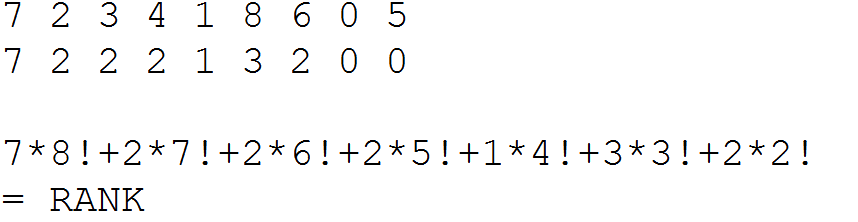
rank还原数组:
类似扫雷般的思路,看当前的a[i],然后就像玩扫雷一样判断每个数(扫雷中毒无法自拔)
exgcd:
用途:求逆元
组合数mod p
1:n,m很小:杨辉三角打表
2:p很小:
lucas定理:

说汉语:
把n,m转为p进制,把每一位的组合数算出来,乘进去,mod p
若出现ni<mi,则说明cnm能被p整除,直接输出0
3.p贼大
阶乘打表+求逆元+暴力
升级版:多次询问
1!~n! mod p:打表
1!~n!mod p的逆元:
求出n!的逆元,i从n到2循环,每次乘i,就是(i-1)!的逆元
线性求逆元:
中国剩余定理

数学公式qaq
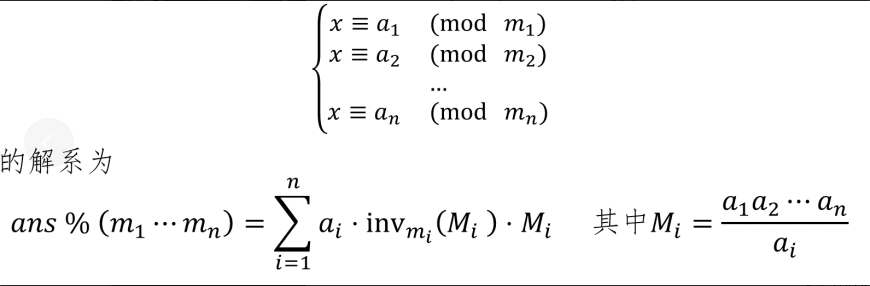
代码什么的先咕咕咕辣




