7.13考试

连暴力都不会写了QAQ

T1:

1.统计

(sum3.cpp)

（sum3.in/out)

时间限制：2s/空间限制：256MB

【题目描述】

小Z喜欢自己研究一些问题，今天老师上课讲了相反数，互为相反数的两个数的和为0，小 Z 现在在考虑三个数的情况，小 Z 现在命名三个互不相同且和为 0 的数为“相反数组”，两个相反数组相同当且仅当两个相反数组的三个数字都相同。

现在给定一组数字，求这组数中有多少个相反数组。

【输入格式】

本题读入为多组测试数据！

本题读入为多组测试数据！

本题读入为多组测试数据！

第一行为数据组数T

对于每组测试数据

第一行为数的个数 N

第二行为 N 个数，有正有负

【输出格式】

输对于每组测试数据，输出有多少个不同的相反数组

【输入输出样例1】

【输入输出样例2】 

【数据规模约定】 

对于30%的数据，1≤T≤10,1≤N≤100

对于70%的数据，1≤T≤10,1≤N≤500

对于100%的数据，1≤T≤50，1≤N≤1000

lyd:这不s*题吗

窝盟可以去个重再搞(因为要用unique所以顺便排了个序，后面有用qwq)

跟咱的思路如此之像qwq,但咱就是没想到二分查找啊qwq

不过咱的玄学优化似乎有用？？？

上面是70分算法

满分算法：

我们发现每次循环j会+1，由于数组有序，所以满足条件的x一定在上一个x的前面。因此我们的从a[n]开始枚举x，一旦发现a[i]+a[j]+x<0,就说明当前的a[j]小了，j就要+1，这样复杂度就降到了nT.

代码长度贼短（from lyd）

#include <cstdio>
#include <algorithm>
const int numsize = 131072;

int T, N;
int a[numsize];
inline int getint() {
    register int num = 0;
    register char ch = 0, last;
    do last = ch, ch = getchar(); while (ch < '0' || ch > '9');
    do num = num * 10 + ch - '0', ch = getchar(); while (ch >= '0' && ch <= '9');
    if (last == '-') num = -num;
    return num;
}

int main() {
    freopen("sum.in", "r", stdin);
    freopen("sum.out", "w", stdout);
    T = getint();
    for (int i = 0; i < T; i++) {
        N = getint();
        for (int i = 1; i <= N; i++)
            a[i] = getint();
        std::sort(a + 1, a + N + 1);//排序
        int cnt = 0;
        N = std::unique(a + 1, a + N + 1) - (a + 1);//去重
        for (int i = 1; i < N; i++) {//枚举a[i]
            int left = i + 1, right = N;//left就是j,a[right]就是上文中的x
            while (left < right) {
                if (a[i] + a[left] + a[right] == 0) {
                    left++;
                    cnt++;
                }
                if (a[i] + a[left] + a[right] > 0) right--;//此时说明x太大，应该向左
                if (a[i] + a[left] + a[right] < 0) left++;//此时应该增加j
            }
        }
        printf("%d\n", cnt);
    }
    return 0;
}//加上快读才40多行的代码

 

T2：

2.二次函数数列

(sequence.cpp)

（sequence.in/out)

时间限制：2s/空间限制：256MB

【题目描述】

我们都知道二次函数的一般形式是，我们打算把二次函数引入到迭代数列的概念中来，得到一个二次函数数列。

那么先来解释一下迭代数列的概念吧：

迭代数列即通过一个函数 和数列的初值来得到数列的每一项：

 

如果这个数列是一个二次函数数列，那么就意味着函数是一个二次函数。

我们都知道是一次函数和常函数时的情况，现在由于一些不可告人的原因我们希望知道它是二次函数时候，数列的通项公式性质。

我们不会要求你算通项公式，但是我们希望你可以计算这个数列的第项来帮助我们的研究，当然数字会很大，我们只需要你返回后的结果。

【输入格式】

读入一共一行，6 个整数

从左到右

 g1,a,b,c,n,p

其中 n 和 p 一定是正整数

【输出格式】

输出一共一行，即答案，答案请不要出现负数。

【输入输出样例1】

 

【输入输出样例2】

【数据规模约定】

对于30%的数据，n不超过 10 ^ 7。

对于100%的数据，n 不超过 10 ^ 17，p 不超过 2 * 10 ^ 6。

 

这个题说的啥呢？就是给出一个数列的第一项，已知这个数列的第i项是f(g_i-1),f是一个二次函数，它三个参数已知，求第n项。

 30pts:暴力O(n)

100pts:我们发现这个p长的很不一般（平常的取模数哪有2e6的？？）

p<2e6,所以这个函数的值域不会超过2e6,但是n远超2e6,所以肯定会有gi=gj,i≠j。当gj=gi时，g_j+1=g_i+1,所以就能构成循环节。我们只要找出这个循环节，基本就做完了。

实现：我们可以写一个死循环，一旦发现循环节或者当前已经算完了第n项就跳出循环，如果是找到循环节，就用n减去循环节前面的一部分，然后对循环节取模，直接输出答案

（代码好写，思路难想到爆炸）

代码from lyd

#include <cstdio>
#include <cstring>
const int mod = 2097152;

int F(long long x, int a, int b, int c, int p) {
    long long ans = 0;
    ans = a * x % p * x % p;
    ans = (ans + b * x % p) % p;
    ans = (ans + c) % p;
    return ans;
}

int g1, a, b, c, p;
long long n;
int f[mod];
int g[mod];

int main() {
    freopen("sequence.in", "r", stdin);
    freopen("sequence.out", "w", stdout);
    scanf("%d %d %d %d %lld %d", &g1, &a, &b, &c, &n, &p);
    g1 = (g1 % p + p) % p;
    a = (a % p + p) % p;
    b = (b % p + p) % p;
    c = (c % p + p) % p;
    memset(g, 0, sizeof(g));
    f[1] = g1, g[g1] = 1;
    int point = 0;
    for (int i = 2; true; i++) {
        if (i > n) break;
        f[i] = F(f[i - 1], a, b, c, p);
        if (g[f[i]]) {
            point = i;
            break;
        }
        g[f[i]] = i;
    }
    if (!point)
        printf("%d\n", f[n]);
    else {
        int m = g[f[point]] - 1, l = point - g[f[point]];
        n -= m;
        n %= l;
        if (n == 0) n = l;
        printf("%d\n", f[m+n]);
    }

    return 0;
}

 

 T3：外星罗盘 

【题目描述】

小H和小Z最近发现了一个神奇的外星罗盘，它的做工十分精美，背景是一副浩大的星空图。就像一个工艺品一般，外星罗盘的本身是一个的棋盘状，为了方便区分出每一个格子，小H和小Z就默认行是从上往下不断增大的，而列是从左到右不断增大的，也就是说你可以认为左上角是,右下角是。

同时罗盘的大部分格子都是光滑的，上面画着一颗行星，但是有些格子很特殊，他们的表面像是故意没有打磨过显得凹凸不平，上面模糊地画着一些小行星带。于是他们将光滑的格子用‘.’来表示，而凹凸不平的格子用‘#’来表示。

罗盘每隔一段时间会有两个光滑的格子突然亮起，一个亮起呈红色，一个呈绿色，然后过一段时间后亮起的格子会熄灭，然后另外两个格子亮起，这样一直反复循环。

小H和小Z觉得这个罗盘一定是在尝试发送什么信息，不过他们也没有思考出任何有效的信息，于是他们打算用这个罗盘玩一个游戏。

他们记录下来了次罗盘的亮灯行为，然后把绿色和红色格子的坐标记录了下来，他们打算研究是否每次绿色坐标都可以只通过往右走和往下走的方式移动到红色坐标，当然凹凸不平的格子是不可以经过的，你也不能神奇的走出棋盘外然后试图从一些神奇的角度绕回来。

【输入格式】(boardgame.in)

一共行。

第一行两个正整数为，表示棋盘迷宫的行列。

接下来行，每行一个长度为的字符串，由‘#’‘.’两种字符组成

接下来1行，一个正整数,表示询问的个数

接下来行，每行四个正整数x1,y1,x2,y2询问绿点（x1,y1）到红点（x2,y2）是否有一条合法的路径

数据保证（x1,y1）（x2,y2）所在的位置都是‘.’，同时x1<=x2,y1<=y2

【输出格式】(boardgame.out)

一共行，每行一个字符串或者，对应每一个询问的答案。

【输入输出样例】

boardgame.in	boardgame.out
4 4 .... ..#. .##. .... 3 2 2 4 4 2 1 4 4 1 2 4 4	No Yes Yes

 

【数据规模约定】

对于40%的数据，N，M≤100，Q≤1000

对于全部的数据，N，M≤500，Q≤1e6

看着这个数据，显然暴力会T成狗对吧。

我们想象怎么降复杂度

暴力的复杂度至少是O(Qn²）的（bfs的复杂度差不多是n²辣）

我们考虑大开脑洞进行优化。

如果我们把整个棋盘分成两半

那么起点和终点有三种情况

①：都在上半部分

②：都在下半部分

③：一个在上面，一个在下面

情况①，②如果继续二分，最终可以转化为情况③。

对于情况③，如果起点可以到达终点，则一定会穿过中间那条线。那我们对于中间那条线上的每一个点，都判断起点能否到达，再判断终点能否到达。如果有一个点，起点和终点都能到达，就说明起点可以到达终点。

 

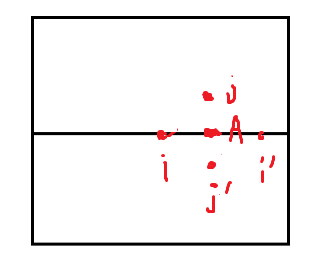
如果我们要判断横线上面的点能否到达点A，我们就可以看能否到达点i或者点j。特别的，对于在中间横线上的点，只需要判断能否到达点i

判断横线下面的点，就可以相当于把路线反过来，看能否到达i'或者j'

但是复杂度好像还是炸了qwq

so我们就需要玄学优化了。我们发现是否能到达是用bool数组表示的，这样就会导致数组很长，循环时间会长。不如我们把8个bool压成1个long long,酱紫就可以减少数组的长度，进而可以跑0.9s过掉这个题

qwq~

思路好口胡，but代码依旧难写的一匹

代码from lyd

#include <cstdio>
#include <vector>
#include <bitset>
using std::vector;
using std::bitset;
const int QUERY_SIZE = 600006;
const int MAP_SIZE = 511;

int N, M, Q;
char map[MAP_SIZE][MAP_SIZE];
int ans[QUERY_SIZE];
bitset<MAP_SIZE> up[MAP_SIZE][MAP_SIZE], down[MAP_SIZE][MAP_SIZE];
struct query {
    int x1, y1, x2, y2, id;
};

query q;
void solve(vector<query> v, int l, int r) {
    int m = (l + r) >> 1;
    if (l > r) return ;//二分出了神奇的东西 
    for (int i = m; i >= l; i--)//对上半部分进行操作 
        for (int j = M; j >= 1; j--) {
            up[i][j] = 0;
            if (map[i][j] == '.') {
                if (i == m) up[i][j].set(j);
                else up[i][j] |= up[i + 1][j];
                if (j != M) up[i][j] |= up[i][j + 1];
            }
        }
    for (int i = m; i <= r; i++)//对下班部分
        for (int j = 1; j <= M; j++) {
            down[i][j] = 0;
            if (map[i][j] == '.') {
                if (i == m) down[i][j].set(j);
                else down[i][j] |= down[i - 1][j];
                if (j != 1) down[i][j] |= down[i][j - 1];
            }
        }
    vector<query> vl, vr;
    for (vector<query>::iterator it = v.begin(); it != v.end(); it++) {
        q = *it;
        if (q.x2 < m) vl.push_back(q);
        else if (q.x1 > m) vr.push_back(q);
        else ans[q.id] = (up[q.x1][q.y1] & down[q.x2][q.y2]).any();
    }
    solve(vl, l, m - 1);
    solve(vr, m + 1, r);
}

int main() {
    freopen("boardgame.in", "r", stdin);
    freopen("boardgame.out", "w", stdout);
    scanf("%d %d", &N, &M);
    for (int i = 1; i <= N; i++)
        scanf("%s", map[i] + 1);
    vector<query> v;
    scanf("%d", &Q);
    for (int i = 0; i < Q; i++) {
        scanf("%d %d %d %d", &q.x1, &q.y1, &q.x2, &q.y2);
        q.id = i;
        v.push_back(q);
    }
    solve(v, 1, N);
    for (int i = 0; i < Q; i++)
        puts(ans[i] ? "Yes" : "No");
    return 0;
}