7.13
1.模拟算法
并不
膜你模拟需要HIGN LEVEL，用蒟蒻的话说，就是在写代码前先想好有哪些坑，整个的结构是个啥。据说不能先写读入输出再像双向bfs一样写中间（神奇的操作）
因为我们是用计算机，所以我们解决完一个题，就力求解决完这一类题。（也就是抽象出来一道题的模型）
我们看一道题压压惊
我们先把这个题抽象出来（也就是HIGH LEVEL）
然后就是按照每个规则判断一遍（恶心的把所有规则写下来）
有了这个模型，就可以想怎么改规则，就怎么改规则了
窝盟在写代码前的思考决定了调试的时间单位qwq
所以一定要想好了再写
（代码一时爽，调试火葬场）
真实的故事：
写完一部分就检查很重要啊
这个还是很有用的。当然在交之前还是要谨慎再谨慎。
还可以来个判断（if(n<0)跑个暴力什么的）
二.贪心
判断贪心：数据范围（线性的一般是贪心（国王游戏这种高精bt除外）），直觉，大胆猜想无需证明
第一步:找规律，找个反例验证
神马是局部最优解？
for example
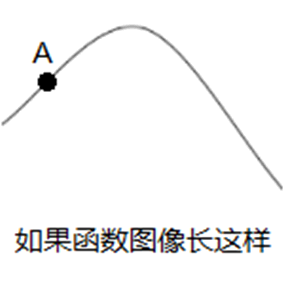
我们不管全局，只管A点周围的一点。当我们走到中间的最高点，A发现往左或往右都会比当前点低，所以A认为当前点就是最高点
如果函数长这样：
那么当A走到了第一个点，就会认为当前点是最大的，这时候就会陷入局部最优的情况
T1:
我们按照价钱从小到大排序，能买的就买，直到没钱。
证明：
①：按照生活常识，我们想省钱对不对？所以我们买便宜的
②：我们假设不这么买，那我们当前有一个k',它可以使一头奶牛高兴，同时它比我们买过的一块巧克力k便宜，这时候我们当然是去买k'咯。所以我们就能够知道要买便宜的。
贪心证明：
①：无需证明，由直觉可得
②：反证法（证明这里就咕咕咕了qwq）
我们可以想到前缀和。这样问题就成了求两个数的差mod M最大。
如果不考虑取模，我们枚举两个数，第一个数就是被减数，第二个数记录当前找到的最小的减数。
我们再考虑取模。取模之后的减法就是两种情况：
对于第一种情况（也就是x-y<m）,我们希望y越小越好，和不取模差不多
对于第二种情况，y当然是越靠近x越好，我们可以维护一个si，记录枚举的x前面比x大的数中最小的数
怎么实现？咕咕咕咕~~~~~~~~
线段覆盖问题（见凌乱的yyy）
按照结束时间排序，
emmm画出来就是酱紫
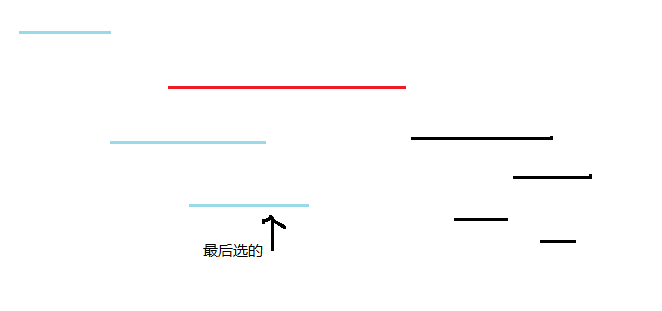
红色为当前线段，蓝色为符合条件的线段
why?因为我们要让线段覆盖尽量长的区间
伪代码如下：
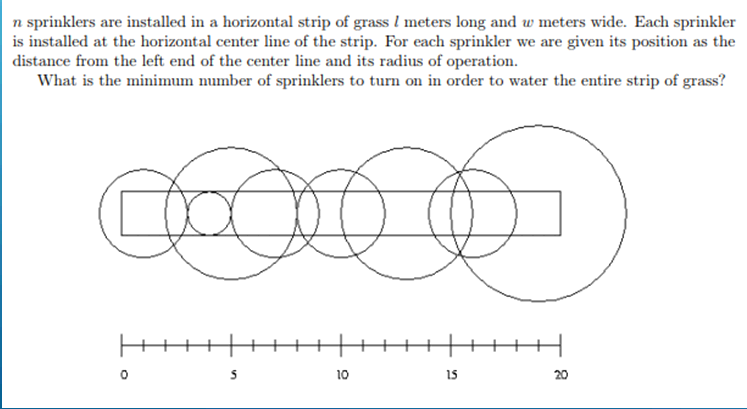
意思就是有一块长方形的草坪（上图中间那个矩形），有n个喷水头，每个喷水头能喷到的范围是一个圆（就是上图的圆），圆心再草坪的宽的一半的那条线上，问最少要几个喷水头才能保证整个草坪都被浇到水。
圆很不好处理，但是在这个题里面圆有用的部分似乎不多。我们不妨研究一下圆的那些地方有用
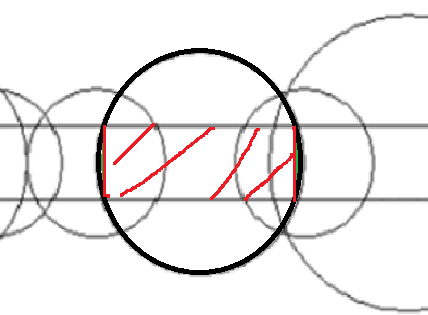
以这个加粗的圆为例，真正有用的部分是红色阴影，绿色部分的贡献可以忽略不计（在这里，可怜的
变成了条线，与矩形没有交的圆就不存在了）
我们发现矩形的宽好像没有什么用
然后每个圆就可以被处理成线段，接下来又是线段覆盖问题，但是和上一题不一样。
这个题要求选择完美覆盖大线段的所有线段
我们可以仿照上题的思路，只不过要考虑的问题与上题完全相反。
那我们还是按照结束时间排序，倒着枚举当前线段，扫描右端点再当前线段左端点右边的线段，找靠左的左端点
画一画：
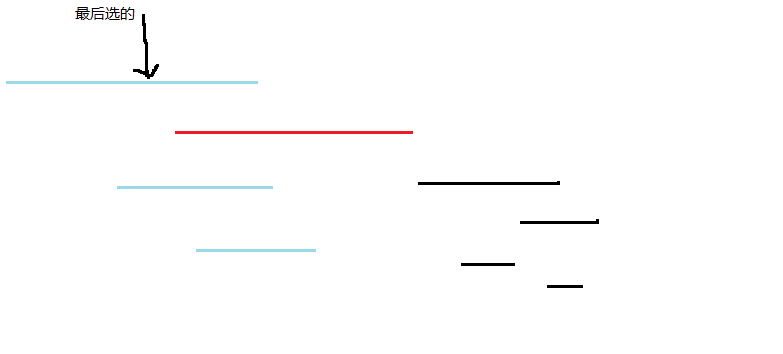
红色为当前线段，蓝色为被扫描到的线段
大意就是x轴是海岸线，在x轴上方有许多小岛，给出固定的雷达半径和小岛坐标，问最少要多少个雷达能覆盖全部小岛，雷达只能放在x轴上。
我们再x轴上画圆是木有希望的，所以我们以岛屿画圆
画的圆会与x轴有两个交点，这两个交点组成的线段内放雷达肯定是能扫到当前的岛屿，那就把岛屿转化成了线段，雷达变成点
那就是转换成有多少个点覆盖所有线段
咋整？
有以下几种情况（接下来的线段都不考虑这条线段之前的情况，假设它们已经弄好了）
1.
好像没什么特殊的，答案直接+1
2.
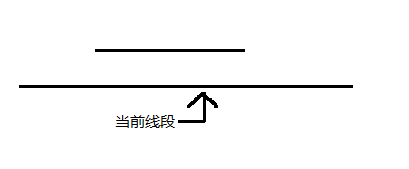发现当前线段里面还有一条更短的线段
3.
相交的如此好看
对于情况2.3，都是转化为考虑较短的那条线段
然后就做完了
实现就咕咕咕了
这里你的血量可以超过初始血量，存在a[i]>d[i]的情况。
真是充满了恶心的一道题。
也就是说打一些怪你的血会比原来的血量高，我们称这些怪为回血怪。而其他a[i]<d[i]的怪我们称之为扣血怪
为了更好的应对毒瘤的扣血怪，我们的血量自然是越高越好，所以我们先打回血怪。
打完所有的回血怪，我们的体力值就到了高峰。
同时我们注意到，如果打完所有的怪（不管你能不能活到那个时候），体力值是一定的。如果这个定值<0,那么肯定不能打完所有的怪
但是定值>0也不代表你能打完
还要判断是否有一个方式能打完怪，但是不好判断
于是我们可以画出来人物的体力值的图像
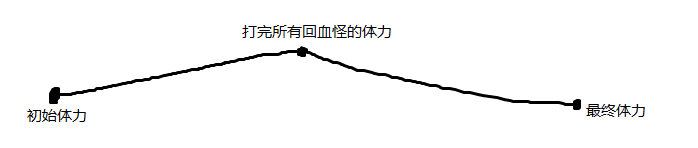
正难则反，顺着不好判断那就倒着来。
从最终体力出发，我们把扣血怪扣掉写当做加血，血瓶加的血当成扣血，这样所有的扣血怪就变成了回血怪,这样我们再判断能不能走回去（中间体力值不会小于0）。
预处理出所有数（<=20）的阶乘，从20的阶乘循环到1的，看输入的数能减哪个就减哪个，最后看能不能到0。
为什么呢?
因为n!>1!+2!+.....+(n-1)!
原理就和转换编码什么的差不多辣
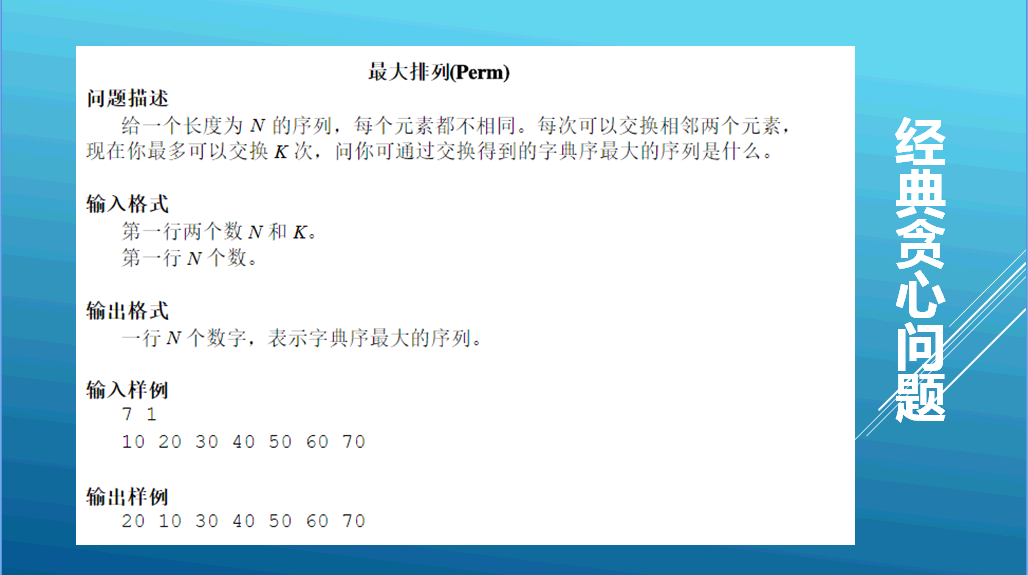
找到最大的往前换？次数不够怎么办
把前k个数中，最大的扔到前面去
就这么做完了
代码永远咕咕咕
