7.9校内考试

又双因为freopen写错少了那么几十分祭

T1:扫雷

简单的来说就是编个程序玩一维扫雷

坑真不少

还没写程序就可以知道的坑

坑1：数据没有保证每个格子上的数据在0到3之间

坑2：数据肯定会有无解的情况（我们输出“No answer会发生什么呢？那就是有55分”）

我们先来玩局扫雷冷静冷静

   （据说四个角上有雷的概率很小）

啊不对是下面这个

我们下面用num[i]表示第i个数，le[i]表示第i个格子上有几个雷

这是样例

 看第一个数字，可以推断出前两个格子都有雷

然后看第一行第三个格子，我们发现由于num[2]=2,le[1]+le[2]=2,所以第三个格子上面没有雷。

我们继续按照上面的方法扫雷,发现3周围的雷只有1个，而num[3]=2,所以le[4]=1

似乎每个格子i上有没有雷依赖于num[i-1]和le[i-1],le[i-2],如果le[i-1]+le[i-2]=num[i-1],就说明num[i-1]已经满足了，i这个格子上就不能有雷了，否则就要有雷。但如果这个格子上有雷，还是达不到num[i-1]，就说明无解。

所以le[i]=num[i-1]-le[i-1]-le[i-2]，当le[i]不为0或1时，就是无解。

这样我们就可以递推求解了

（思路by ych,%%%ych orz）

然鹅坑还木有踩完

坑3：如果num[1]≠2或者num[1]≠0(也就是前两个放什么不能确定),我们就要分两类讨论：

①：le[1]=1,le[2]=0.

②：le[1]=0,le[2]=1

也就是按照第一个格子是否有雷来讨论。

坑4：在坑3的情况下，如果n<3，还要特判（如果n=2,num[1]=1,num[2]=1应该输出什么我也不知道，反正没有这组数据）

坑5：因为要分情况讨论，所以我们在判断是否有解的函数中，如果无解不能直接输出无解。

坑6：分类讨论完别忘了memset

我们可以用前面得到的递推式来求解，过程中一旦有le[i]不为0或1，则无解，最后还要再判断第二行每个格子周围的le[i]相加是否等于num[i]。

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int n,le[10009],num[10009];
bool bj1,bj2;
bool emm()//判断函数
{
    bool a=0;
    for(int i=3;i<=n;i++)
    {
        le[i]=num[i-1]-le[i-1]-le[i-2];
        if(le[i]<0||le[i]>1)
        {
        return false;
        }
    }
    for(int i=3;i<=n;i++)//一定要有这个
    {
        int sum=0;
        int st=i-1;//st可以不要，和后面的end对应比较优雅
        int end=i+1;
        if(i==n)end=n;//处理i=n的情况
        for(int j=st;j<=end;j++)
        {
            sum+=le[j];
        }
        if(sum!=num[i])
        {
            return false;
        }
    }
    return true;
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
     {
         num[i]=read();
         if(num[i]>3||num[i]<0)
         {
             printf("No answer");return 0;//防止毒瘤数据
        }
     }
    if(num[1]>2||num[n]>2)
    {
        printf("No answer");return 0;
    }
    if(n==2)//我猜没有n=0的情况就没写
    {
        if(num[1]==0)
        {
            if(num[2]==0)
             printf("0 0");
            else printf("No answer");
            return 0; 
        }
        if(num[1]==1)
        {
            if(num[2]==1)
             printf("1 0");
            else printf("No answer");
            return 0;
        }
        if(num[1]==2)
        {
            if(num[2]==2)
            printf("1 1");
            else printf("No answer");
            return 0;
        }
    }
    if(n==1)
    {
        if(num[1]<2)printf("%d",num[1]);
        else printf("No answer");
        return 0;
    }
    if(num[1]==2)//以上都是对n的判断
    {
      le[1]=1;le[2]=1;
      if(emm())
      {
          for(int i=1;i<=n;i++)
           printf("%d ",le[i]);
          return 0; 
      }
      else {printf("No answer");
      }return 0;    
    } 
    if(num[1]==0)
    {
        le[1]=0;le[2]=0;
        if(emm())
        {
        for(int i=1;i<=n;i++)
           printf("%d ",le[i]);
          return 0; 
        }
        printf("No answer");
         return 0;
    }
    if(num[1]==1)
    {
        le[1]=0;le[2]=1;
        if(emm())//分情况讨论
        {
        for(int i=1;i<=n;i++)
           printf("%d ",le[i]);
          return 0; 
        }
        else
        {
            memset(le,0,sizeof(0));
            le[1]=1;le[2]=0;
            if(emm())
            {
             for(int i=1;i<=n;i++)
                   printf("%d ",le[i]);
                 return 0; 
            }
            printf("No answer"); 
            return 0;
        }
    }
}

（原谅我原来的坑爹代码打死不会改了）

蒟蒻太弱了，写的超长（ych的代码超短的说）

T2:极值

乍一看没什么思路。

打个表找找规律？

（1≤k≤100）

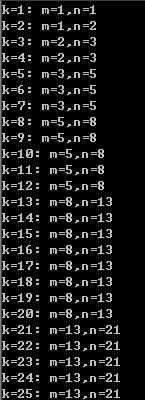
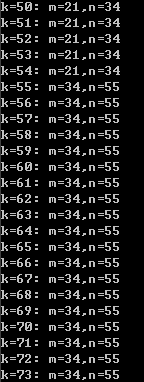
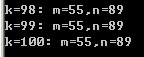
好长一张表ρωρ

不难发现这好像是斐波那契数列

先求一个斐波那契数列的前缀和。加到第几项大于等于k时，就输出这斐波那契数列的这一项和下一项。而且数据只有1e9,不需要矩阵快速幂。

代码很好写，但问题来了，它为什么是斐波那契数列？

（证明 by ybr）

(n²-mn-m²)²=1

(m²+mn-n²)²=1

(m²+mn+mn-mn+n²-2n²)²=1

[(m+n)²-mn-2n²]²=1

[(m+n)²-n(m+n)-n²]²=1

最后一个式子就是第一个式子的形式,所以它是斐波那契数列

证毕。

代码：

#include<cstring>
#include<cmath>
#define ll long long
using namespace std;
int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int k,m,n,z;
ll f[59]={0,1};
ll fb[59]={0,1};
int main()
{
   freopen("mn.in","r",stdin);
   freopen("mn.out","w",stdout);
   k=read();
   for(int i=2;fb[i-1]<=k;i++)
   {
        fb[i]=fb[i-1]+fb[i-2];
        f[i]=f[i-1]+fb[i];
        if(f[i]>=k)
         {
             z=i;break;
      }
   }
   fb[z+1]=fb[z]+fb[z-1];
   printf("%lld %lld",fb[z],fb[z+1]);   
}

T3 15数码问题

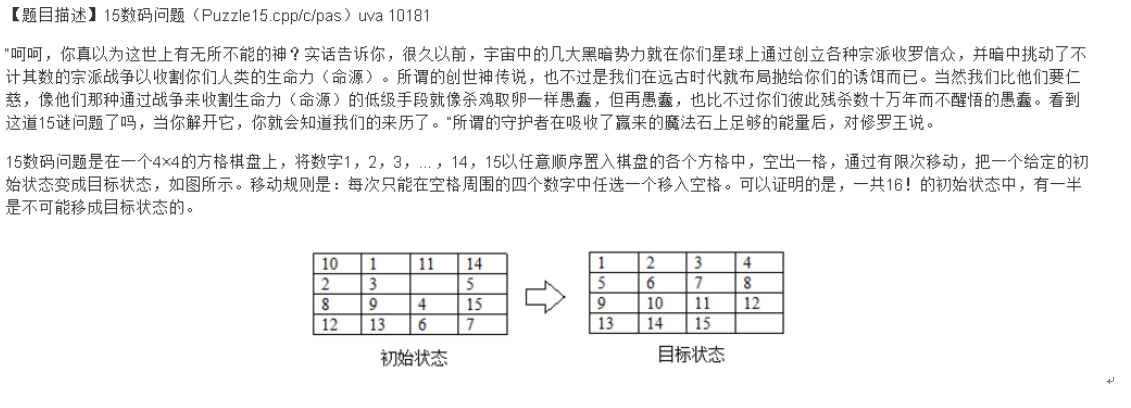
奥赛佳句醒目

这个是个什么东西呢？

就是这货：

依旧是玩小游戏（我都不会玩写个鸟程序）

然而数据水的一匹

两个点全无解，第一个点是样例，60pts直接送（freopen又炸了的人表示崩溃）

我们先来讨论讨论如何在神马都不会的题上骗分（毕竟在考场上推正解难于上青天）

1.输出样例（挑出样例输入中几个典型的数据作为判定依据）（万一就有样例分呢？？？）

2.打表找规律（就像T2一样，一次多打几个）

3.相信奇迹输出无解

4.爆搜（我是真的不会）

好了我们来讲正解。

因为题目说有一半的状态是无解的，所以我们可以先判断是否有解。

判断是否有解：

我们这里规定i逆序数是i前面所有数中，比i小的数的个数。

一个神奇的定理：

N×N的棋盘，N为奇数时，与八数码问题相同。

N为偶数时，空格每上下移动一次，奇偶性改变。称空格位置所在的行到目标空格所在的行步数为空格的距离（不计左右距离），若两个状态的可相互到达，则有，两个状态的逆序奇偶性相同且空格距离为偶数，或者，逆序奇偶性不同且空格距离为奇数数。否则不能。

证明：一位ID为 tiaotiaoyly的大佬的博客（这里面还讨论了三维的）

虽然能去掉一半的状态，但是16!/2的状态数量我们也承受不了。

所以接下来我们考虑剪枝。

直接搜索50步可能会搜出很多奇奇怪怪的不是最优解的状态，而且当前数据的解可能在50步以内，这样多搜索的步数就会造成很大的浪费，所以我们一步一步的放宽搜索步数的上限（开始是2）。那么为什么不会TLE呢？

我们想一棵搜索树，它的节点是指数级增加的。所以叶子节点的数量就和其他节点的数量差不多了，并且每次搜索每个节点只搜一次。因此不会TLE

当然我们还要继续剪枝。

在这里我们计算每个数与它的目标状态的最小距离，也就是最少走的步数x。如果当前已经走的步数+x>当前限制的步数，就说明在这次搜索是打死都不能把它移动到目标状态了，就返回。

据说这叫迭代加深搜索

std代码：