P1058立体图(面对代码解释)



样例:
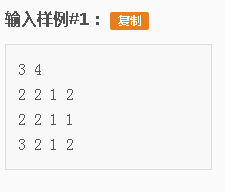
输出样例:

(洛谷上面的那个太丑了就不放了)
乍一看好像真的没有什么思路
所以我们结合ybr大佬的代码进行分析
疑点都将在代码下面进行分析(面对代码做题模式开始)
#include<cstdio> #include<iostream> using namespace std; int read(){ int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') { ans=(ans<<1)+(ans<<3)+(ch^48); ch=getchar(); } return last=='-'?-ans:ans; } char c[1001][1001],c1[10][10]= {//倒着存储 "+---+", "| |/", "| | +", "+---+ |", " / /|", " +---+", };//6行7列 的方块 int n,m,jz[51][51],maxh=-1,maxl=-1,zbx,zby; inline void fg(int zbx,int zby)//覆盖操作 { for(int i=0;i<=4;i++)c[zbx][zby+i]=c1[0][i];//这里是逐行覆盖 for(int i=0;i<=5;i++)c[zbx+1][zby+i]=c1[1][i]; for(int i=0;i<=6;i++)c[zbx+2][zby+i]=c1[2][i]; for(int i=0;i<=6;i++)c[zbx+3][zby+i]=c1[3][i]; for(int i=1;i<=6;i++)c[zbx+4][zby+i]=c1[4][i];//为什么从1开始?因为考虑到不在立方体内的空格要变成"." for(int i=2;i<=6;i++)c[zbx+5][zby+i]=c1[5][i];//从2开始同上 } int main() { m=read();n=read(); for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) { jz[i][j]=read(); } } for(int i=1;i<=m;i++)//从输入的矩阵的左上角开始,满足先后,先左 for(int j=1;j<=n;j++) { zbx=(m-i)*2+1;zby=(m-i)*2+1+4*(j-1);//待会解释 for(int k=1;k<=jz[i][j];k++,zbx+=3) { fg(zbx,zby); } if(zbx+2>maxh)maxh=zbx+2;//我不知道为什么 (by ybr)(下面有解释) if(zby+6>maxl)maxl=zby+6; } for(int i=maxh;i>=1;i--)//上面计算zbx是默认原点是(1,1),不是(0,0) { for(int j=1;j<=maxl;j++) { if(c[i][j]=='\0') printf(".");//如果c[i][j]没有被覆盖过,就输出"." else printf("%c",c[i][j]); } printf("\n"); } return 0; }
难点:1:zbx,zby是个啥玩意?
(zbx,zby)枚举当前的这个块的左下角在输出的图中的坐标

就是枚举这个蓝点辣
注意我们把最终输出的立体图当做二维图来看

推导:
zbx:(我们先考虑只有一层的情况)
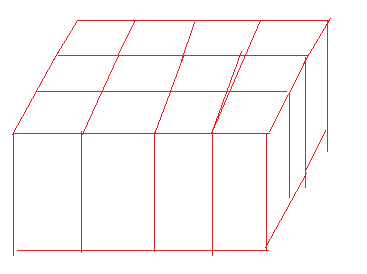
我们注意到,一个字符在上面的x轴上的贡献是1,(x轴就是上面说的x轴)
m-i:
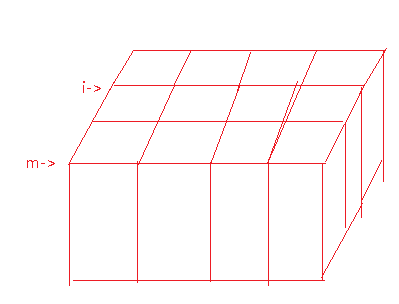
(不要在意没有画完的最右边)
从上图看出来,m-i就是m和i隔着几“行”,其中,一“行”在x轴上的贡献是2,所以要(m-i)*2,因为一个块的边对x的贡献都是2,我们要先+2,再-2,就抵消了。
又因为下标是从1开始计算,所以要+1
每往上摞一层,zbx就要+3(一层对x轴的贡献是3)
zby:
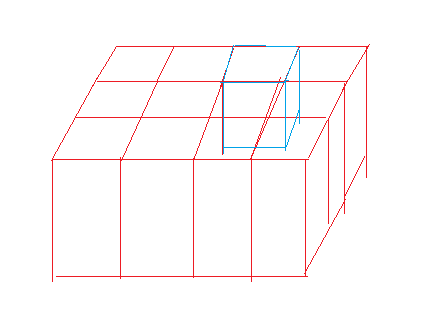
我们拿那个蓝色的方块举例。
因为一个方块在y轴方向上的贡献是4(这里的贡献不会重复计算),所以不考虑"."的贡献,当前的zby是(j-1)*4+1
再通过肉眼观察,发现在输出图中,是"+"的那一行最左边的"."的数量都是偶数,“.”对y轴的贡献是(m-i)*2
难点2:maxh?maxl?为毛这俩的更新方法如此玄学?
ybr:我也不知道为什么
咳咳我们来研究一下这个玄学的问题
窝盟先来分析一下zby+6是个什么鬼
分析如下:

一张手动补全的图
我们看到,在第一行的方块左下角在y轴上的坐标+6就是最终输出图的最右端
zbx+2:
由于代码在执行取maxh,maxl之前有以下神奇的操作
for(int k=1;k<=jz[i][j];k++,zbx+=3) { fg(zbx,zby); }
这就是看每一个格子上面有几个方块
在执行完神奇的操作之后,原本表示左下角的zbx变成了左上角(可以手画一下)
由于一个![]() 在x轴上的贡献是2,所以是zbx+2
在x轴上的贡献是2,所以是zbx+2
难点3:这是什么存储方法怎么好像是倒着的?
它的确是倒着的
难点4:这是什么个覆盖顺序???
从后往前枚举(i是从1到m,因为第1行在最里面),从左往右枚举,从下往上枚举
好了解释完了qwq(逃





