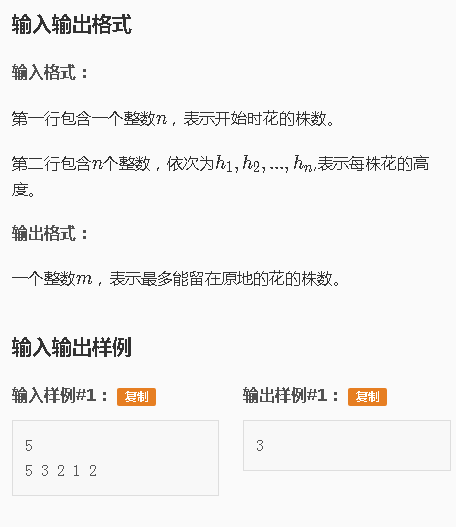
P1970花匠

传送

首先，这道题据说是一个dp

其次，贪心就能做

我们先来看好想好写的贪心

按照题目来，所有偶数点要么都是凸的，要么都是凹的，不能有凸有凹。我们把每株花的高度都在平面直角坐标系中点出来，再连线。这样我们就得到了若干条直线。在直线上的点（不包含波峰&波谷）都是单调的，要么加上不满足偶数点是凹/凸的，要么就改变了后面偶数点的凹凸性。所以在直线上的点都不选。这样我们把所有的波峰，波谷都选下来，就是最终的答案了。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,a[100009],ans;//1↑,0↓ 
int no,l;
int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int main()
{
 
    n=read();
    for(int i=1;i<=n;i++)
     a[i]=read();
    if(a[2]>a[1])l=1;//l记录a[i-1]对于a[i-2]是增还是减
    if(a[2]<a[1])l=0;
    if(a[1]!=a[2])ans=1;
    for(int i=2;i<=n;i++)
    {
      if(a[i]==a[i-1])continue;    //如果高度一样，就不管
      no=-2;
      if(a[i]>a[i-1])no=1;//no记录a[i]对于a[i-1]是增是减
      if(a[i]<a[i-1])no=0;
      if(no!=l)ans++;//如果增减性变化，就说明出现波峰（波谷）
      if(no!=-1)l=no;
    }
    ans++;
    printf("%d",ans); 
}

再来看正解的dp

dp[i][0]代表这个点在删完花后的序列里，是下降时最多保留的花的数量

dp[i][1]代表是上升是最多保留的花的数量（还是在删完花的序列里）

其中，dp[i][o]=dp[i-1][1]+1.dp[i][1]=dp[i-1][0]+1,因为要使最终的序列是个波浪形的，就必须前一个降，后一个升（或者反过来）。

dp[i][0]=max(dp[i][0],dp[i-1][0]),dp[i][1]=max(dp[i][1],dp[i-1][1])

初始化：dp[1][0]=1,dp[1][1]=1

代码：

#include<bits/stdc++.h>
using namespace std;
int n,a[100009],dp[100009][2],ma1,ma0;
int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
int main()
{
    
    n=read();
    for(int i=1;i<=n;i++)
     a[i]=read();
    dp[1][0]=1;dp[1][1]=1;
    ma1=1,ma0=1;
    for(int i=2;i<=n;i++)
    {
        if(a[i]>a[i-1])dp[i][1]=dp[i-1][0]+1;
        if(a[i]<a[i-1]) dp[i][0]=dp[i-1][1]+1;
        ma1=max(dp[i][1],ma1);
        ma0=max(dp[i][0],ma0);
        dp[i][1]=ma1;
        dp[i][0]=ma0;
    }
    printf("%d",max(dp[n][1],dp[n][0])); 
}