线段树板子1（洛谷P3372）
传送
一道线段树板子（最简单的）
似乎之前在培训里写过线段树的样子？不记得了
何为线段树？
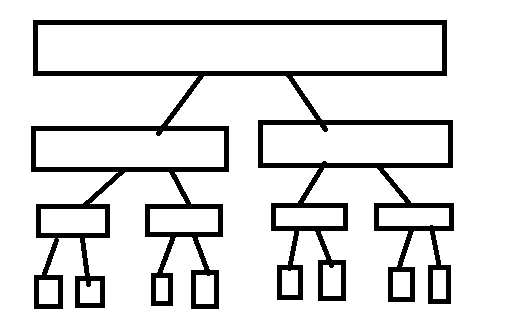
一般就是长成这样的树，树上的每个节点代表一个区间。线段树一般用于区间修改，区间查询的问题。
我们如何种写一棵线段树？
线段树包含：
1.建树
2.区间修改
3.区间查询与懒标记下传
---------------------------------------------------------------------
一些定义：
sum[k]:节点k所代表的区间的区间和（k是节点编号）
val[i]:在1到n的区间中，点i的权值
laz[k]:在k节点上打的懒标记
1.建树
从根节点开始，递归分别建左子树和右子树，当l=r时，sum[k]=val[l].我们注意到，对于每个不是叶子的节点来说，它的sum值为它的左二字+它的右儿子。同时线段树是一颗二叉树，所以节点k的左儿子的编号就是k*2,右儿子是k*2+1。所以，sum[k]=sum[k*2]+sum[k*2+1]。
2.区间修改
如果一个区间[l,r]要进行修改，那么与[l,r]有交集的节点都要修改。考虑到与[l,r]有交集的节点数为log(r-l+1)(如果出错欢迎指正)，如果直接修改每个点，则复杂度会很高，况且修改了以后还不一定会被查询到。为了降低复杂度，我们采用懒惰的思想。这时候，我们就有了懒标记。
在节点k上打上懒标记，代表k的子树中所有节点都加上laz[k],k节点的sum变为真实值。不过暂时先不真的在左右儿子节点加，如果查询到了，再加。这是待会要讲的标记下传。
所以，对于区间修改来说，我们唯一要做的就是找到被修改区间完全包含的区间，在这个节点上打个懒标记，然后维护一下打上标记的节点的sum(sum[k]+=laz[k]*(r-l+1))，就ok了。
如果当前区间并没有完全被包含，则继续递归寻找。判断它的左右儿子哪个与修改区间有交集，就修改哪个儿子，直到有完全被包含的区间出现。同时，对于当前的这个节点来说，还是要维护sum,sum[k]=sum[k*2]+sum[k*2+1](就是当前节点的sum=左儿子的sum+右儿子的sum)
3.区间查询与懒标记下传
当区间查询的时候，就不能再懒下去了（该干活了），这时候，我们就要把laz[k]扔给它的左儿子，右儿子，让他们变成真实值。
当然，如果没有懒标记（laz[k]=0）,那就直接结束了，就不管了。
如果当前区间并不完全被包含在查询区间里面，则递归查询。（要先懒标记下传）看它的哪个儿子与被查询区间有交集，就递归哪个儿子。
也正是因为上述原因，懒标记一次只下传一层（没有传到而要用到的节点会在递归查询中下传到）
在懒标记下传中，把懒标记传给它的左右儿子（不管是否与被查询区间有交集）。让它左右儿子的laz加上laz[k],然后维护他左右儿子的sum。(sum[2*k]+=laz[k]*(mid-l+1),sum[2*k+1]=laz[k]*(r-mid))
这样一棵线段树的基本操作就讲完辣。
代码：
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> using namespace std; const long long N=100009;//小心毒瘤数据范围 long long n,m,val[N*4],sum[N*4],laz[N*4];//注意数组大小 long long read()//读入long long(防毒瘤数据) { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } if(f)x=-x; return x; } int read2()//读入int(为了和函数的参数相匹配) { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } if(f)x=-x; return x; } void zj(int k,int l,int r,int v)//标记下传时候的增加（其实可以写进标记下传函数里面） { laz[k]+=v; sum[k]+=v*(r-l+1); } void pushdown(int k,int l,int r)//标记下传 { if(laz[k]==0)return ; long long mid=(l+r)>>1; zj(k<<1,l,(int)mid,laz[k]);//位运算优化常数 zj(k<<1|1,(int)mid+1,r,laz[k]); laz[k]=0; } void add(int k,int l,int r,int x,int y,int v)//将[x,y]这段区间加上v,l,r为当前递归到的节点代表的区间的左，右端点，k为当前节点编号 { if(l>=x&&r<=y) { laz[k]+=v; sum[k]+=v*(r-l+1); return; } long long mid=(l+r)>>1; pushdown(k,l,r); if(x<=mid) add(k<<1,l,(int)mid,x,y,v); if(mid<y) add(k<<1|1,(int)mid+1,r,x,y,v); sum[k]=sum[k<<1]+sum[k<<1|1];// 维护和！！！ return; } long long query(int k,int l,int r,int x,int y)//查询 { if(l>=x&&r<=y)//[l,r]被[x,y]完全覆盖 { return sum[k]; } long long mid=(l+r)>>1,ans=0; pushdown(k,l,r); if(x<=mid)//判断儿子是否有交集 ans+=query(k<<1,l,(int)mid,x,y); if(mid<y) ans+=query(k<<1|1,(int)(mid+1),r,x,y); return ans; } void build(int k,int l,int r)//建树 { if(l==r) { sum[k]=val[l]; return; } long long mid=(l+r)>>1; build(k<<1,l,(int)mid); build(k<<1|1,(int)(mid+1),r); sum[k]=sum[k<<1]+sum[k<<1|1]; return; } int main() { n=read();m=read(); for(int i=1;i<=n;i++) val[i]=read(); build(1,1,n); for(int i=1;i<=m;i++) { int cz,x,y; cz=read2();x=read2();y=read2(); if(cz==1)//修改 { int k=read2(); add(1,1,n,x,y,k); } else//查询 { printf("%lld\n",query(1,1,n,x,y)); } } return 0; }
线段树2（添加乘法操作，更带感）
