P1983车站分级

%%%rqy

传送

我们注意到题目中这段话：

既然大于等于x的站都要停，那么不停的站的级别是不是都小于x？(这里讨论在始发站和终点站以内的站(注意这里是个坑))

我们可以找出每趟车没停的站，向所有停了的站建一条边，表示没停的站的级别<停了的站的级别，同时记录所有的站的入度

这样，一开始入度为0的站级别就是1。

对于那些入度不为0的点来说，它们的级别就是所有指向它的点中，级别最大的那个点的级别+1

for example

 

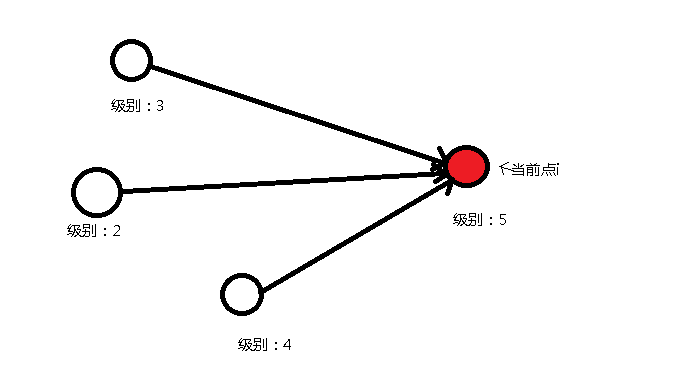
 因为每个级别为a车站x不一定只有级别为a-1的车站向x连边。

那程序怎么实现呢？

据大佬说要跑拓扑排序（%%%ych）

简单的说：

先将所有入度为0的点入队，遍历它们的每条出边，将所有到达的点的入度-1。如果有入度为0的点，就将其入队，并且它的级别为当前出队的点的级别+1。当队空时，拓扑排序结束。

这样为什么能保证达到上图的效果呢？因为对于任意一点i来说，如果当前出队的点为j,若存在有连接i且级别比j大的点k,则k此时入度一定不为0（还没遍历j的出边时），就可以保证先算k的级别，再算i的级别了。

复杂的说，走这里

跑完拓扑排序，我们将所有点的级别sort一遍，找最大的，就是答案。

小坑见代码

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
int aans,n,m,s[1005][1005],in[1005],head[1005],cnt,ans[1005];
bool jb[1005][1005];//b[i][j]为i到j是否建过边（不建重边）
queue <int> q;
struct Edge{
    int to,next;
}edge[10000005];//开大点（我也不知道最多有几条边，总之开小了会wa）
void add(int fr,int to)//前向星存图
{
    cnt++;
    edge[cnt].to=to;
    edge[cnt].next=head[fr];
    head[fr]=cnt;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
     {
      scanf("%d",&s[i][0]);
      bool rr[1005];int start,end;
      memset(rr,0,sizeof(rr));
      for(int j=1;j<=s[i][0];j++)
      {
        scanf("%d",&s[i][j]);
        rr[s[i][j]]=1;//标记每个点是否到达
        
      }start=s[i][1];end=s[i][s[i][0]];
       for(int j=start;j<=end;j++)//注意一定是讨论始发站和终点站以内的车站（见样例）
       {
           if(!rr[j])
            {  
                for(int k=1;k<=s[i][0];k++)
                {
                    if(!jb[j][s[i][k]])//不建重边
                {add(j,s[i][k]);
                    in[s[i][k]]++;//建边的时候统计入度
                    jb[j][s[i][k]]=1;
                }
            }
         }
       }    
     }
     for(int i=1;i<=n;i++)
      {
       if(!in[i])
       {
       q.push(i);
       ans[i]=1;
       }
      }
     while(!q.empty())//跑拓扑排序
     {
         int u=q.front();
         q.pop();
         for(int i=head[u];i;i=edge[i].next)
         {
             in[edge[i].to]--;
             if(in[edge[i].to]==0)
             {
              q.push(edge[i].to);
              ans[edge[i].to]=ans[u]+1;
             }
        }
     }
     sort(ans+1,ans+1+n);
     printf("%d",ans[n]);   
}