校内测试618
今天是618
题目:(只做前三题)
T1多项式输出


既然题目中系数按从高到低开始输出,那我们从n到1开始存
具体见代码
#include<iostream>//评测机拒绝万能头 #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int a[105],n; int main() { //freopen("poly.in","r",stdin);考试别忘写 //freopen("poly.out","w",stdout); scanf("%d",&n); for(int i=n;i>=0;i--) scanf("%d",&a[i]); for(int i=n;i>=0;i--)//i即为当前x的指数 { if(i!=n&&a[i]>0)printf("+");//注意输出的第一项没有加号 if(a[i]==-1&&i!=0)printf("-"); if(a[i]!=0&&a[i]!=1&&a[i]!=-1)printf("%d",a[i]);//如果abs(a[i])==1 ,则不输出1(-1) if(i>1&&a[i]!=0)printf("x^%d",i);//i为1时只输出x if(i==1&&a[i]!=0)printf("x"); if((a[i]==1||a[i]==-1)&&i==0)printf("%d",a[i]); } return 0; }
T2:分数线划定

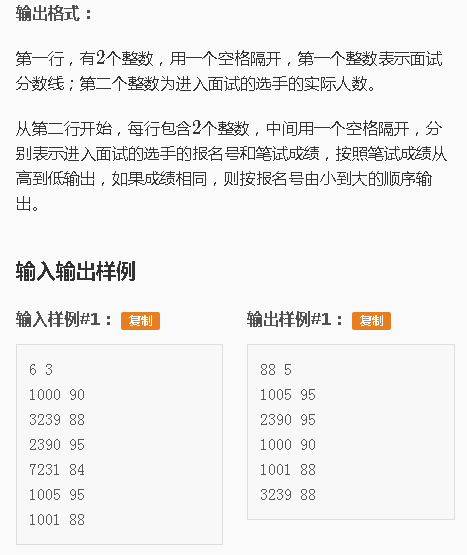
特别注意画黄线的部分!!!(忘记输出,结果100分没了QAQ)
简单来说,读入完之后先排序,算出k=m*1.5后注意会有分数相同的人,如果有分数相同的人,就一直m+1。最后输出小坑见代码。
#include<iostream>//评测机不喜欢万能头 #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int n,m; struct rr{ int bh,f; }r[5005]; bool cmp(rr a,rr b) { if(a.f!=b.f)return a.f>b.f; return a.bh<b.bh; } int main() { // freopen("score.in","r",stdin); // freopen("score.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d%d",&r[i].bh,&r[i].f); sort(r+1,r+1+n,cmp); int mm=(double)m*1.5; int k=mm; while(r[k].f==r[mm].f)k++; if(r[k].f!=r[mm].f)k--;//其实可以直接写成k-- printf("%d %d\n",r[k].f,k); for(int i=1;i<=k;i++) {printf("%d %d\n",r[i].bh,r[i].f); } return 0; }
T3:细(zhi)胞(bi)分(fen)裂(li)



数据那么大,显然是一道数学题
仔细思索,把题目翻译一下,对于每个si,求m1^m2|si^k的k的最小值。
我们看到数据范围,显然硬求会爆炸,那我们不妨分解一下质因数
对m1和每个输入的si分解质因数后,逐一比较m1与s的每个质因子的次数。
当然,如果有一个m1有的质因子,si没有,那就不用往下继续算了。
若si^k能被m1^m2整除,则对于s的每个质因子qi来说,它的次数ai一定大于m1的qi的次数bi,而且细胞每次分裂,对每个ai来说,都相当于加上一个最初的ai(刚分解完质因数的ai)。这时,问题转换为对每个ai求c*ai>=bi,c的最大值。
再从所有的c中,找出最小的那个,就是答案。若最后的答案没有被更新过,就输出-1。
特殊情况:m1=1 这时无论si怎样都可以在0秒内均分
代码
代码中有一些unbelievable的地方
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #include<cstring> using namespace std; //1.m1,所有的s质因数分解(m1的所有质因数的次数*m2) //2.比较每个s与m1分出的质因数的次数(没包含全,直接continue),用m1的次数/s的次数向上取整,找出每个最大,将每个最大取最小 //3.特判试管==1 int m2,n,ans=2147483647; struct pri{ int all,ys[30005],cs[30005],zhi;//ys[i]是第i个质因数,cs[i]是第i个质因数的次数,zhi就是m1,s的值,all是一共有几个不同的质因数 }m1,s; void fj(pri &kk)//分解质因数 { memset(kk.ys,0,sizeof(kk.ys)); memset(kk.cs,0,sizeof(kk.cs)); for(int i=2;i*i<=kk.zhi;i++) { if(kk.zhi%i==0) { kk.all++; kk.ys[kk.all]=i; kk.cs[kk.all]=1; kk.zhi/=i; while(kk.zhi%i==0) { kk.cs[kk.all]++; kk.zhi/=i; } } } if(kk.zhi>1) {kk.ys[++kk.all]=kk.zhi; kk.cs[kk.all]++; } } int main() { scanf("%d",&n); scanf("%d%d",&m1.zhi,&m2); if(m1.zhi==1){printf("0\n");return 0;}//小心有坑 fj(m1); for(int i=1;i<=m1.all;i++) {m1.cs[i]*=m2; } for(int i=1;i<=n;i++) { scanf("%d",&s.zhi); s.all=0; fj(s); if(s.all<m1.all)continue;//如果s的质因数的种数还没有m1多,则s肯定不能包含所有m1有的质因数 int aans=0; bool flag=0;int ss=1; if(s.all>=m1.all)//其实这句可以去掉的说 { for(int j=1;j<=m1.all;j++) { while(ss<=s.all&&s.ys[ss]<m1.ys[j])++ss; if(ss>s.all||s.ys[ss]>m1.ys[j])break;//如果有一个质因数s没有,就不用继续算下去了 int h=m1.cs[j]/s.cs[ss]; if((m1.cs[j]%s.cs[ss]))h++;//注意这里用ceil会出现一些unbelievable的事情,比如说你会wa if(h>aans)aans=h;//取最大值 if(j==m1.all)flag=1; else flag=0; } } if(flag) ans=min(ans,aans);//所有最大值中取min } if(ans==2147483647)ans=-1;//未被更新,则证明没有细胞能满足条件 printf("%d",ans); }
终于搞完了qwq
T4:道路游戏
此题木有做,先咕咕咕着


