5.1培训考试一

又一次爆0 QAQ

爆0次数++

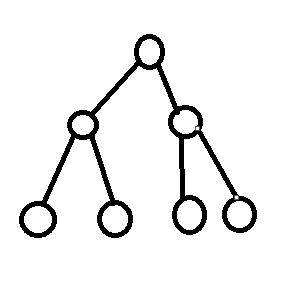
任意两点的最近公共祖先的深度便是包含这两个点且根节点最深的子树的根的深度。我们反过来想一想，一个节点是多少点对的最近公共祖先（这里算对答案贡献）？是这个点为根的子树的点数的平方。因为每一对算两次（lca[i][j]和lca[j][i]）（lca[i][i]除外）

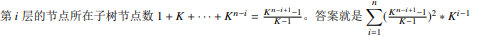
化简用到的是等比数列求和公式

这是60分的式子

#include<iostream>
#include<cstdio>
using namespace std;
long long fa[998224],all,q[998224];
const int mod=998244353;  
int n,k;
inline long long ksm(long long a,long long b)
{long long r=1;
   while(b)
   {if(b&1)r=(r%mod)*(a%mod)%mod;
    a=(a*a)%mod;
    b/=2;
   }
   return r;
}
int main()
{ 
  cin>>n>>k;
  long long ans=0;
  for(int i=1;i<=n;i++)
  {long long an=ksm(k-1,mod-2)%mod;//分步求上面的式子，注意模意义下除法要转换为求逆元（这里用费马小定理+long long）
   long long bn=ksm(k,n-i+1)%mod-1;
   bn=(((an*bn)%mod)*((an*bn)%mod))%mod;
   an=(bn%mod)*(ksm(k,i-1)%mod);
   an%=mod;
   ans+=an;
   ans=(ans+mod)%mod;//别忘了转换成正数
   } 
  printf("%lld",ans);
}

我们还要继续化简刚才的式子。

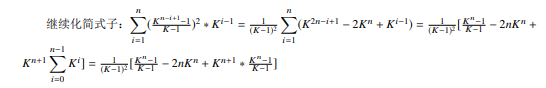
这里中括号是取整。

//from wyx
#include <bits/stdc++.h>

using namespace std;

const int mod = 998244353;
typedef long long LL;
int fpm(int p, int k)
{
    int res = 1;
    for (p %= mod; k; k >>= 1, p = (LL) p * p % mod)
        if (k & 1) res = (LL) res * p % mod;
    return res;
}
int main()
{
    freopen("lca.in", "r", stdin);
    freopen("lca.out", "w", stdout);
    int n, K; cin >> n >> K;
    int e = fpm(K - 1, mod - 2); //(K - 1) ^ (-1)
    int x = (fpm(K, n) - 1) * (LL) e % mod; //(K ^ n - 1) / (K - 1)
    int ans = (fpm(K, n + 1) + 1) * (LL) x % mod;
    ans = (ans - 2 * n * (LL) fpm(K, n)) % mod;
    ans = ans * (LL) e % mod * (LL) e % mod;
    cout << (ans < 0 ? ans + mod : ans);
}

暴力做法：求出s,t,s的反串，t的反串四个的公共子串。这里求反串是为了保证回文。

时间复杂度O(n^2*m^2)

显然它太暴力了。我们怎么优化呢？

代码from wyx

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int maxn = 100005;

int n, m, nex[maxn][26], ans;
char a[maxn], b[maxn], c[maxn];

bool pal(int l)
{
    for (int i = 1, j = l; i < j ; i++, j--)
        if (c[i] != c[j]) return false;//如果不是回文串，就返回false
    return true;
}
void solve(int stp, int l, int cur)//stp为当前的s串的下标，l是t的下标，
{
    if (l + m - stp + 1 <= ans) return ;
    if (stp > m) {if (pal(l)) ans = l; return ;}
    solve(stp + 1, l, cur);
    if (int t = nex[cur][b[stp] - 'a'])
        c[l + 1] = b[stp], solve(stp + 1, l + 1, t);
}
int main()
{
    scanf("%s", a + 1); n = strlen(a + 1);//从下标1开始存
    scanf("%s", b + 1); m = strlen(b + 1);
    for (int i = n - 1; i >= 0; i--)//构造自动机
    {
        for (int j = 0; j < 26 ; j++)//26个字母
            nex[i][j] = nex[i + 1][j];//初始化
        nex[i][a[i + 1] - 'a'] = i + 1;//原序列中的第i+1个字母出现在i+1的位置
    }
    solve(1, 0, 0); printf("%d", ans);
    return 0;
}

这道题防AK ------Jelly Goat

这道题最简单了 ------wyx

据说出题人有个神奇的习惯，那就是第一题巨难，最后一题巨简单qwq

我们先来看一下洛谷那道均分纸牌

题目描述

有

移牌规则为：在编号为

现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。

例如

①

移动

从 ③ 取

输入输出格式

输入格式：

两行

第一行为： $\le N \le 1001≤N≤100）$

第二行为： $A_1,A_2, … ,A_nA1,A2,…,An （NN堆纸牌，每堆纸牌初始数，1 \le A_i \le 100001≤Ai≤10000）$

输出格式：

一行：即所有堆均达到相等时的最少移动次数。

输入输出样例

输入样例#1：

4
9 8 17 6

输出样例#1：

在这里，我们先求出所有纸牌的平均数，然后将每堆纸牌比平均数多的部分（如果少，就视为多负数张牌）,移到旁边的牌堆上答案就是 ∑每次移动的张数的绝对值（要注意考虑第i堆要加上第i-1堆移过来的数量再减去平均数）

让我们回到考试题。我们可以参考上面的思路，计算出来每堆牌要向下一堆移动的数量|∑ak-∑bk|(k从1到i)。但又因为这里一次只能移动13张或者5张,这里设t=|∑ak-∑bk|,所以把一堆牌移动到合法的次数不定方程13a+5b=t的解a,b的绝对值之和。

画个图,演示一下洛谷的思路

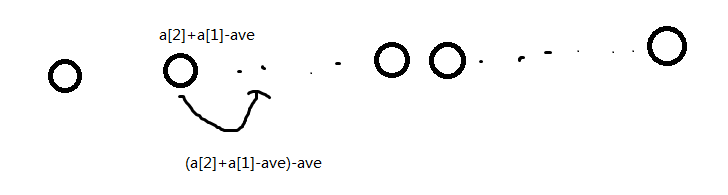
演示的就是上面每一堆移动为什么是|∑ak-∑bk|，这里的bk就是洛谷里面的ave(平均值)

我们要让总的次数最小，就得让单次最小。我们先用exgcd求出一组解a0,b0，通解就是：

a=a0-5k

b=b0+13k

k∈Z

为了让|a|+|b|最小，显然在a进行-5k后变号或者是b进行+13k后变号时的a,b满足要求

也就是：

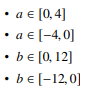
代码 from wyx
#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int maxn = 100005;
const LL inf = 1ll << 50;
int n; LL a[maxn], b[maxn], now = 0, ans = 0;

LL xabs(LL x) {return x < 0 ? -x : x;}
LL calc(LL t) {//其实我们这里不用exgcd,直接枚举a和b就行（因为我们知道了a,b的范围）
    LL res = inf;
    for (LL a = -4; a <= 4; a++)
        if ((t - a * 13) % 5 == 0) res = min(res, xabs(a) + xabs((t - a * 13) / 5));
    for (LL b = -12; b <= 12; b++)
        if ((t - b * 5) % 13 == 0) res = min(res, xabs(b) + xabs((t - b * 5) / 13));
    return res;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
    for (int i = 1; i <= n; i++) scanf("%lld", &b[i]);
    for (int i = 1; i <= n; i++)
        now += a[i] - b[i], ans += calc(now);
    printf("%lld", ans);
}

老师的代码太强惹%%% orz

posted @ 2019-05-05 15:49 千载煜阅读(164) 评论(0) 编辑收藏举报

刷新页面返回顶部

千载煜

5.1培训考试一

题目描述

输入输出格式

输入输出样例

公告