堆
堆是完全二叉树的一种。
所谓完全二叉树,就是每一个有孩子的节点一定有左孩子的二叉树
举几个例子
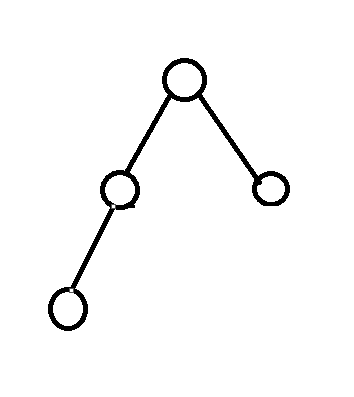
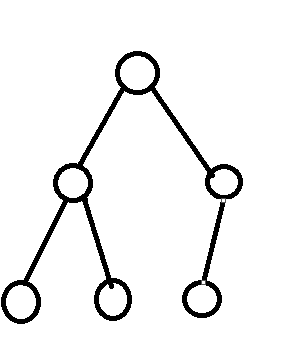
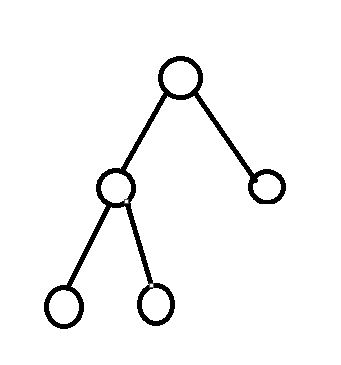
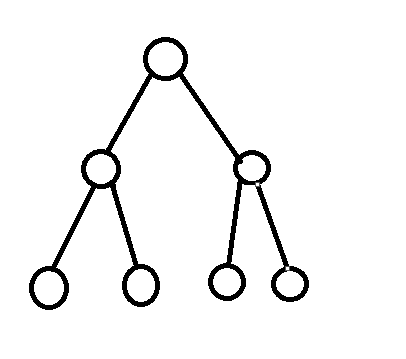
上面都是完全二叉树,最后一个是满二叉树,也是完全二叉树
而下面的就不是
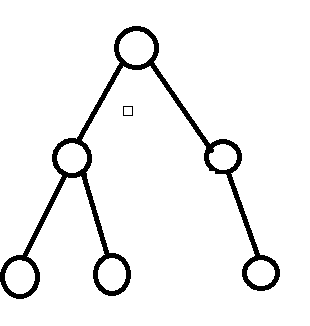
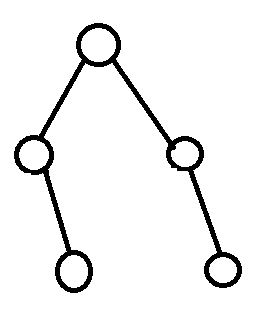
完全二叉树的结构方便存储。若我们设一个节点的编号为i,那么不难发现它的左孩子是2i,右孩子是2i+1,它的父亲是i/2(整除),这方便我们用一维数组模拟。
小根堆:
对于任何一个节点i来说,a[i/2]<=a[i]且a[i]<=a[2*i],a[i]<=a[2*i+1](如果存在左右孩子的话)
即每个节点的值必定大于等于其父节点,小于等于其子节点。
大根堆:
将小根堆反过来即为大根堆。
不难看出,堆是要动态维护的。所以我们如何将一个数加入到堆里/从堆里取出呢?
加入(这里是小根堆):
1. 在堆尾先加入一个元素,并将该节点置为当前节点i。
2. 将i与i/2比较,如果小于,就交换,并将当前节点编号改为i,继续如此比较。如果大于,就结束。(我们称之为上浮)
int cnt=0; void put(int x) { a[++cnt]=x; int m=cnt; while(m>=1) {int next=m/2; if(a[m]>=a[next])break;//如果满足小根堆,就停止循环 swap(a[m],a[next]); m=next; } }
大根堆的加入就把>=改为<=即可
取出:
1.将根节点取出,并将a[cnt]放到根节点的位置上。
2.比较该节点的两个儿子(特判没有儿子的情况),将该节点与较小的儿子比较,如果大于,就交换,继续如此比较。如果小于,就停止。
int get() {int m,next,r; r=a[1]; a[1]=a[cnt--]; while(m*2<=cnt) {next=m*2; if(a[next]>a[next+1]&&next+1<=cnt)next++;//如果右儿子比左儿子小并且右儿子存在,
//就比较当前点和右儿子 if(a[m]<a[next])break; swap(a[m],a[next]); m=next; }
return r;//这里是取出,上面是维护堆 }
大根堆依旧是将比较符号改过来。
应用:堆排序。


