一本通之最短路径

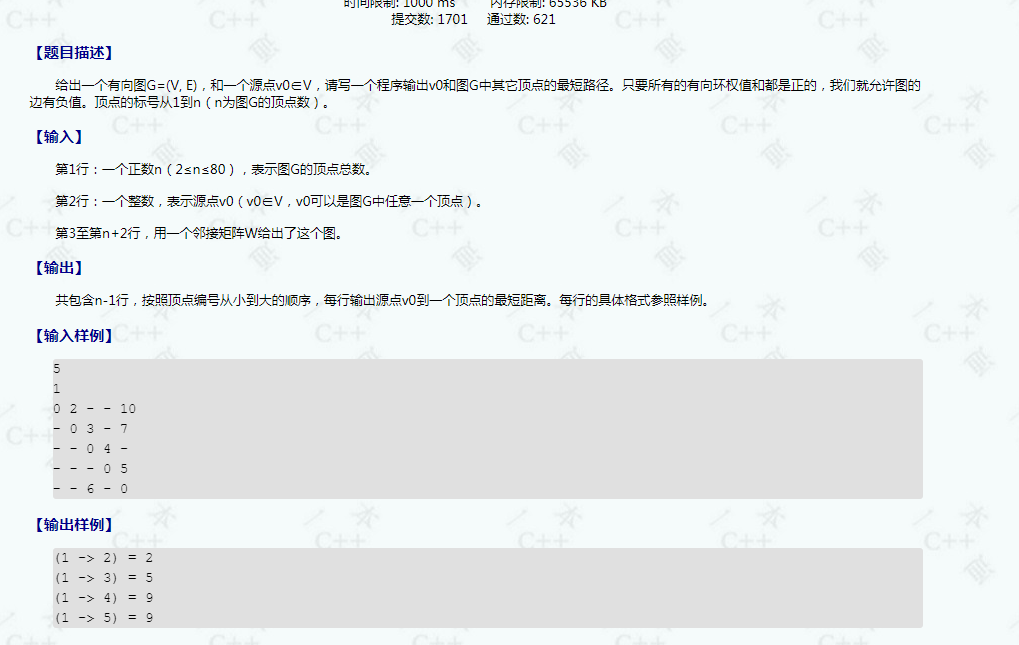
一个从输入就开始恶心人的题目~~~~~~~~~~~~

显然我们要判断邻接矩阵中的数字并把它赋值给g[i][j]。

介绍个神奇的东西

if是个神奇的函数。当用scanf输入时，有格式占位符。把这两个东西神奇的组合一下，可以判断当前输入的字符是否是整数。

代码如下：

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int main()
{int k; 
 if(scanf("%d",&k))cout<<"true"<<endl;
  else cout<<"false"<<endl;
}

输入3，输出true

输入 38，输出true

输入k,输出false

这个与快读的判断相比，如果数据是两位数，就不用再计算了。

解决输入，接下来就是求最短路径

因为要求1到每个点的最短路径，所以用floyed比较方便

代码如下

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int g[101][101],n,m;
const int inf=0x7ffffff;
int main()
{scanf("%d%d",&n,&m);
  for(int i=1;i<=n;i++)
   {for(int j=1;j<=n;j++)
     g[i][j]=inf;
     g[i][i]=0;
   }
for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            int b;
            if(scanf("%d",&b)==1)//如果b是整数
                a[i][j]=b;
            else
                a[i][j]=INF;
        }
    }
  for(int k=1;k<=n;k++)
  {for(int i=1;i<=n;i++)
    {for(int j=1;j<=n;j++)
      {if(g[i][j]>g[i][k]+g[k][j])
        g[i][j]=g[i][k]+g[k][j];
      }
    }
  }
  for(int i=1;i<=n;i++)
  {if(i!=m)
    printf("%d->%d = %d\n",m,i,g[m][i]);
  }
}