平衡二叉树和应用场景
腾讯公司昨日接受记者采访的平衡二叉树二叉树的排序,绝对是歧视。汗...
平衡二叉树称为平衡树,由Adelson-Velskii和Landis至1962首次提出,它也被称为AVL树。
他的定义是非常easy,1,此二叉树即是平衡二叉树。把二叉树的每一个节点的左子树减去右子树定义为该节点的平衡因子。
二叉平衡树的平衡因子仅仅能是1、0或者-1。
平衡二叉树是对二叉搜索树(又称为二叉排序树)的一种改进。二叉搜索树有一个缺点就是,树的结构是无法预料的。任意性非常大。它仅仅与节点的值和插入的顺序有关系。往往得到的是一个不平衡的二叉树。在最坏的情况下。可能得到的是一个单支二叉树,其高度和节点数同样,相当于一个单链表。对其正常的时间复杂度有O(lb n)变成了O(n)。从而丧失了二叉排序树的一些应该有的长处。
当插入一个新的节点的时候。在普通的二叉树中不用考虑树的平衡因子,仅仅要将大于根节点的值插入到右子树,小于节点的值插入到左子树,递归就可以。
而在平衡二叉树则不一样,在插入节点的时候,假设插入节点之后有一个节点的平衡因子要大于2或者小于-2的时候,他须要对其进行调整。如今仅仅考虑插入到节点的左子树部分(右子树与此同样)。主要分为下面三种情况:
(1)若插入前一部分节点的左子树高度和右子树高度相等。即平衡因子为0。插入后平衡因子变为1。仍符合平衡的条件不用调整。
(2)若插入前左子树高度小于右子树高度。即平衡因子为-1,则插入后将使平衡因子变为0,平衡性反倒得到调整,所以不必调整。
(3)若插入前左子树的高度大于右子树高度。即平衡因子为1。则插入左子树之后会使得平衡因子变为2,这种情况下就破坏了平衡二叉树的结构。所以必须对其进行调整,使其加以改善。
调整二叉树首先要明确一个定义。即最小不平衡子树。最小不平衡子树是指以离插入节点近期、且平衡因子绝对值大于1的节点做根的子树。
以下解说平衡二叉树最主要的4种调整操作,调整的原则是调整后他的搜索二叉树的性质不变,即树的中序遍历是不会改变的:
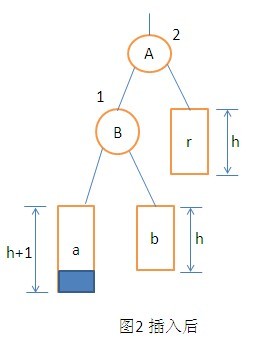
1. LL型调整。
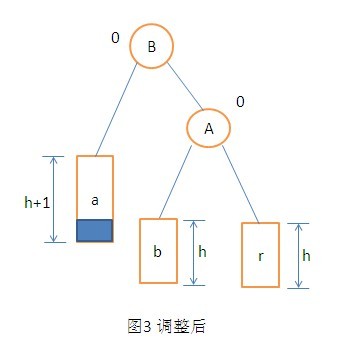
在B点的左子树上插入一个节点。插入后B点的左子树的平衡因子变为1。A节点的平衡因子变为了2。这样能够看出来A节点为根节点的子树是最小不平衡子树。
调整时,将A的左孩子B向右旋转取代A称为原来不平衡子树的根节点。将A的节点右下旋转称为B的右子树的根节点,而B的原右子树变为A的左子树。具体步骤例如以下图:

2. RR型调整操作
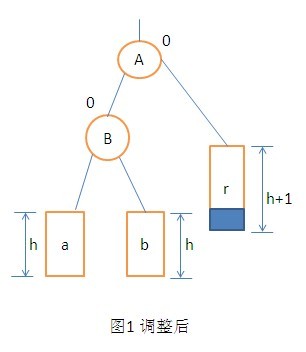
在A节点的右孩子的右子树上插入节点。使得A节点的平衡因子由-1变为-2而引起的不平衡所进行的调整操作。调整操作大致一样。看图就能够明确了。


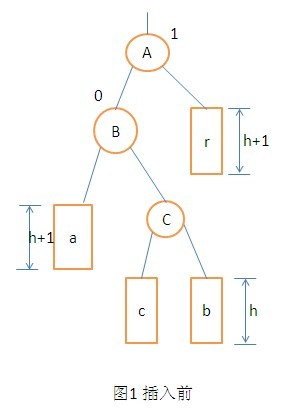
3. LR型的调整操作。在A节点的左孩子的右子树上插入节点。使得A节点的平衡因子由1变为了2而引起的不平衡所进行的调整的操作。调整过程如图:

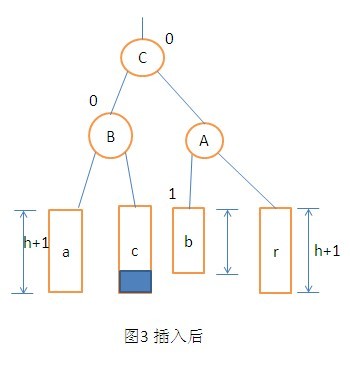
4. RL型的调整操作。不多说了,直接上图:
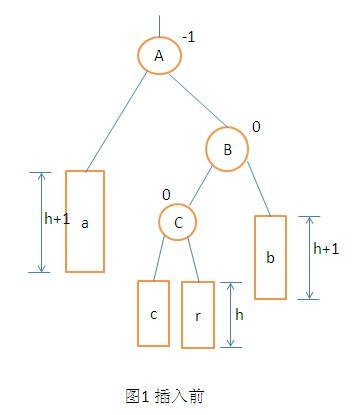


在二分搜索树的插入和删除计算,它有一个平衡树的优势:使树结构是更好,从而提高了速度查找操作。其缺点是:插入和删除操作复杂,从而降低了它们的操作速度。
不平衡的二叉搜索树的删除操作引起的比插入节点复杂的局面节点。这将不讨论。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号