count

一个数在modP意义下有逆元当且仅当这个数与P互质，否则无论成什么数都不能成一

且逆元有且只有一个

所以只要统计P之前的（不含P）与P互质的数的个数 s

但因为有可能算两次，所以找出所有x*x=1(mod P) 个数是t

答案就是（s+t）/2

而这个P之前与P互质的数的个数就是欧拉函数

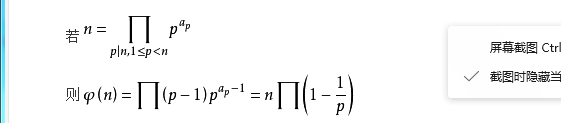
分解质因数

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <string>
 4 #include <cmath>
 5 #include <iostream>
 6 #include <algorithm>
 7 #include <map>
 8 #include <set>
 9 #include <queue>
10 #include <vector>
11 using namespace std;
12 typedef long long ll;
13 typedef unsigned int uint;
14 typedef unsigned long long ull;
15 typedef pair<int, int> PII;
16 #define fi first
17 #define se second
18 #define MP make_pair
19 
20 ll read()
21 {
22     ll v = 0, f = 1;
23     char c = getchar();
24     while (c < 48 || 57 < c) {if (c == '-') f = -1; c = getchar();}
25     while (48 <= c && c <= 57) v = (v << 3) + v + v + c - 48, c = getchar();
26     return v * f;
27 }
28 
29 int main()
30 {
31     freopen("count.in", "r", stdin);
32     freopen("count.out", "w", stdout);
33     ll n = read();
34     ll _n = n, phi = n;
35     for (ll i = 2; i * i <= _n; i++)
36         if (_n % i == 0)
37         {
38             phi = phi / i * (i - 1);
39             while (_n % i == 0)
40                 _n /= i;
41         }
42     if (_n > 1)
43         phi = phi / _n * (_n - 1);
44     ll s = 0;
45     for (ll i = 1; i < n; i++)
46         if (i * i % n == 1)
47             s++;
48     printf("%lld\n", (phi + s) / 2);
49 }

 欧拉定理求逆元

 

posted @ 2018-10-23 17:45  lcan  阅读(294)  评论(0)  编辑  收藏  举报