work
1.二维DP
f[i][j]选第i台,已经选了j
倒着
f[i][j]=f[i+1][j+1],f[i+1][0]
- 1d1d的才能优化（状态，转移都是一维的），状态是二维一一定有n^2个数，所以不能优化
2.贪心
- 最优化DP不会做，贪心，两个三个贪心取最大值
3.一维DP
dp[i]<-dp[j]+e[j+1]+e[j+2]+......+e[i-1] dp表示不选的，这样最后不能直接得出答案，在前面和后面各加上一个e为0的就可以了
这段长度一定是一个定值，枚举这个值
状态1d 转移n*k
优化
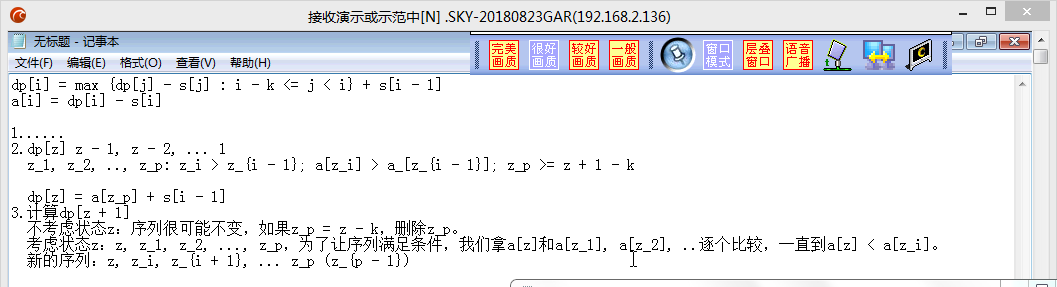
- DP优化思路：单调栈， 单调队列，数据结构，斜率优化
dp[i]=max{dp[j]-sum[j] }+sum[i-1]
令a[j]=dp[j]-sum[j]
- 动态求区间最大值 O(nlogn)
- 1.线段树，st表（加一个东西，重新更新）
- 2.单调队列
dp[0],dp[1]->dp[i]...
- 筛选根本不可能更新的状态
队列满足两个单调性（->单调队列），每个状态最多被删掉一次，O(n),
整个算法O(n)
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 typedef long long ll; 5 const int maxn=1e5+7; 6 ll n,k; 7 ll e[maxn],sum[maxn],f[maxn][3]; 8 int main(){ 9 cin>>n>>k; 10 for(int i=1;i<=n;i++){cin>>e[i];sum[i]=sum[i-1]+e[i];} 11 f[1][0]=0;f[1][1]=e[1]; 12 for(int i=2;i<=n;i++){ 13 f[i][0]=max(f[i-1][1],f[i-1][0]); 14 for(int j=1;j<=k;j++){ 15 if(i-j<0) continue; 16 f[i][1]=max(f[i][1],f[i-j][0]+sum[i]-sum[i-j]); 17 } 18 } 19 cout<<max(f[n][0],f[n][1])<<endl; 20 return 0; 21 }
我的30分代码，就是想到要把sum[i]提出来，用单调队列维护......
std:
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 using namespace std; 6 7 typedef long long ll; 8 9 const int N = (int)1e5; 10 typedef long long ll; 11 typedef int arr[N + 10]; 12 13 int n, K, f, r; 14 arr q; 15 ll e[N + 10], dp[N + 10]; 16 17 int main() { 18 scanf("%d %d", &n, &K); 19 for (int i = 1; i <= n; ++i) scanf("%lld", e + i), e[i] += e[i - 1]; 20 21 q[f = r = 1] = 0, dp[0] = 0; 22 23 for (int i = 1; i <= n + 1; ++i) { 24 if (q[f] < i - K - 1) ++f; 25 dp[i] = dp[q[f]] + e[i - 1] - e[q[f]]; 26 for ( ; r >= f && dp[q[r]] - e[q[r]] <= dp[i] - e[i]; --r); 27 q[++r] = i; 28 } 29 30 cout << dp[n + 1] << endl; 31 return 0; 32 }
1.要注意f[i]表示的是i不选，所以前后各加一个e为0的点，这个转化要能想到
也只有f[i]表示i不选才可以，要不没法写......
对我来说，nk的DP能想出来都很不容易，要注意把学的东西用到考试中，这种把相同的东西提出来，然后滑动窗口的夏令营貌似讲过，听课啊......
今天晚上听课又不好，听课的提高比做题有效多了
TAT
单调队列的写法 head tail的初值设置
