sub

 

求逆序对是枚举一个数，统计前面有多少数小于它

这个用乘法原理，统计左右小于或大于它的

要用树状数组，但数太大数组开不下，要离散化

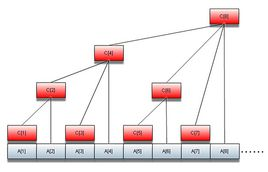
A[0]存储的是是0的数有多少个

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 typedef long long ll;
 5 const ll mod = 1e9 + 7;
 6 int n;
 7 int tmp[200005], a[200005];
 8 int bit1[200005], bit2[200005];
 9 
10 inline int lowbit(int x){
11     return x & -x;
12 }
13 
14 void add(int *bit, int pos, int v){
15     for(int i = pos; i <= n; i += lowbit(i)){
16         bit[i] += v;
17     }
18 }
19 int query(int *bit, int pos){
20     int ret = 0;
21     for(int i = pos; i; i -= lowbit(i)){
22         ret += bit[i];
23     }
24     return ret;
25 }
26 ll ans = 0;
27 int main(){
28     scanf("%d", &n);
29     for(int i = 1; i <= n; i ++){
30         scanf("%d", &a[i]); tmp[i] = a[i];
31     }
32     sort(tmp + 1, tmp + n + 1);
33     for(int i = 1; i <= n; i ++){
34         a[i] = lower_bound(tmp + 1, tmp + n + 1, a[i]) - tmp;
35         add(bit2, a[i], 1);
36     }
37     for(int i = 1; i <= n; i ++){
38         add(bit2, a[i], -1);
39         ans = (ans + 1ll * query(bit1, a[i] - 1) * (query(bit2, n) - query(bit2, a[i]))) % mod;
40         ans = (ans + 1ll * query(bit2, a[i] - 1) * (query(bit1, n) - query(bit1, a[i]))) % mod;
41         add(bit1, a[i], 1); 
42     }
43     printf("%lld\n", ans);
44     return 0;
45 }

 树状数组求逆序对的这种方法暑假在清北就听过，然而什么都不记了...

这是能力的问题，更是态度的问题

posted @ 2018-08-25 17:18  lcan  阅读(242)  评论(0)  编辑  收藏  举报