20172306 2018-2019-2 《程序设计与数据结构》实验二报告
20172306 2018-2019-2 《程序设计与数据结构》实验二报告
课程:《程序设计与数据结构》
班级: 1723
姓名: 刘辰
学号:20172306
实验教师:王志强
实验日期:2018年11月11日
必修/选修: 必修
1.实验内容
-
实验一:实现二叉树
参考教材p212,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试 -
实验二:中序先序序列构造二叉树
基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能,比如给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试 -
实验三:决策树
自己设计并实现一颗决策树 -
实验四:表达式树
输入中缀表达式,使用树将中缀表达式转换为后缀表达式,并输出后缀表达式和计算结果(如果没有用树,则为0分) -
实验五:二叉查找树
完成PP11.3 -
实验六:红黑树分析
参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树(TreeMap,HashMap)进行源码分析,并在实验报告中体现分析结果。
(C:\Program Files\Java\jdk-11.0.1\lib\src\java.base\java\util)
2. 实验过程及结果
实验一:实现二叉树的过程及结果
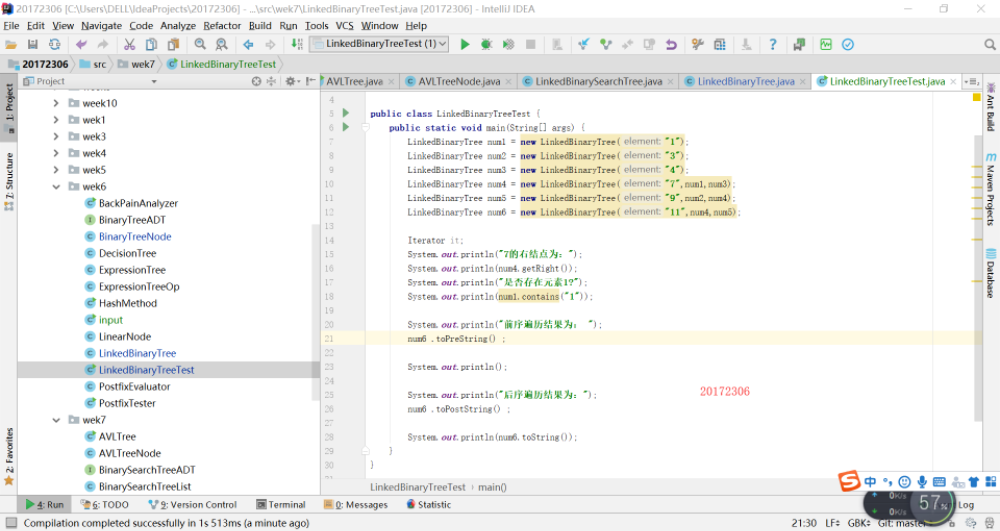
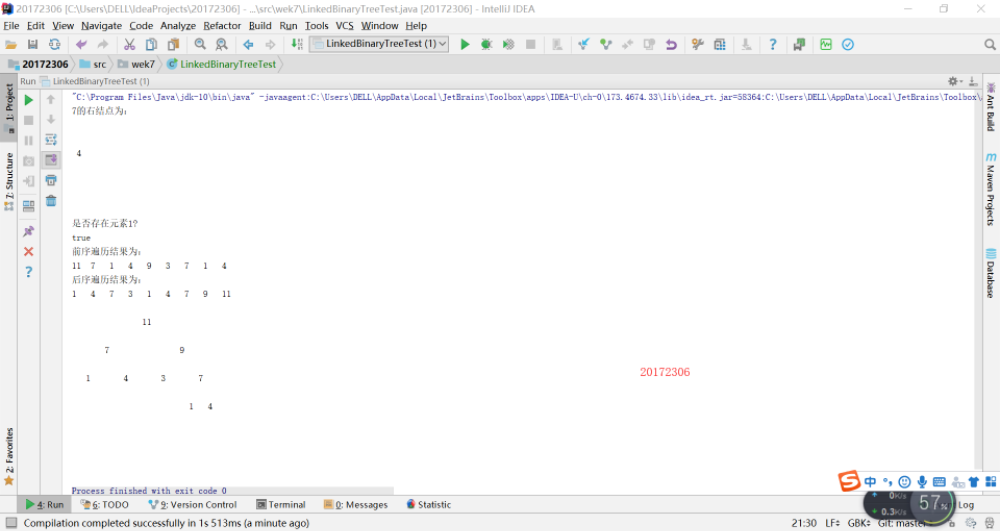
实验二:中序先序序列构造二叉树的过程及结果

实验三:决策树的过程及结果
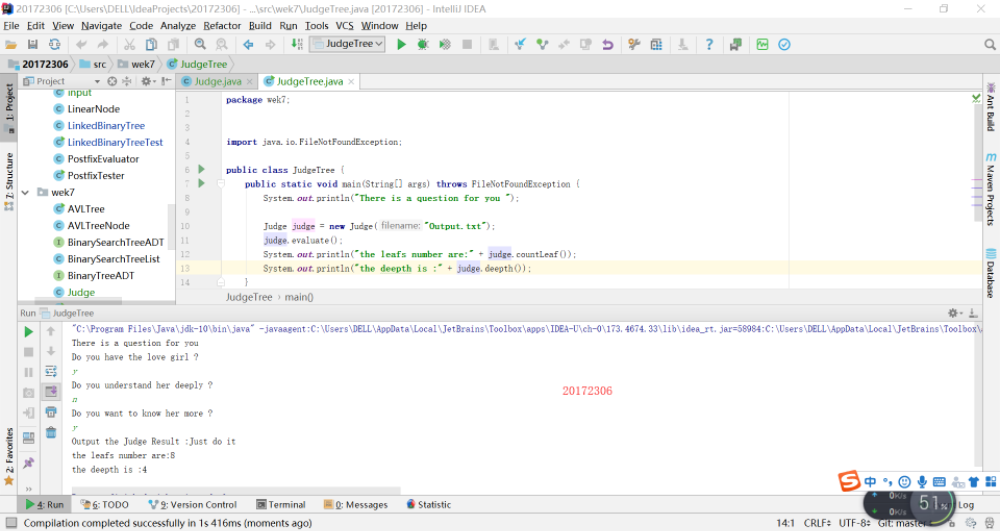
实验四:表达式树的过程及结果
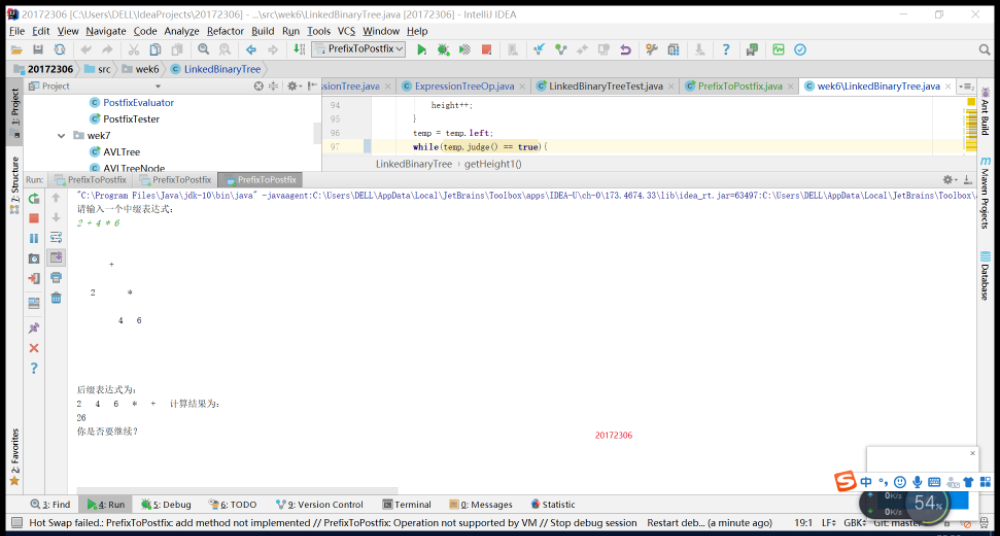
实验五:二叉查找树
实验六:红黑树分析(其实看了代码好长啊,但是很多都是注释,注释太长了)
-
先再了解一下红黑树的主要特点:
- 每个节点都只能是红色或者黑色
- 根节点是黑色
- 每个叶子节点是黑色的
- 如果一个节点是红色的,则它的两个子节点都是黑色的
- 从任意一个节点到每个叶子节点的所有路径都包含相同数目的黑色节点
-
TreeMap和HashMap的区别:
- TreeMap的key是有序的,增删改查操作的时间复杂度为O(log(n)),为了保证红黑树平衡,在必要时会进行旋转,在TreeMap中用的是Comparator,Comparator一般表示类在某种场合下的特殊分类,需要定制化排序
-
Comparator的接口
public interface Comparator<T> {
int compare(T o1, T o2);
boolean equals(Object obj);
}
- HashMap的key是无序的,增删改查操作的时间复杂度为O(1),为了做到动态扩容,在必要时会进行resize。在HashMap中用的是Comparable,Comparable一般表示类的自然序
- Comparable接口
public interface Comparable<T> {
public int compareTo(T o);
}
- TreeMap
- (1)put方法
首先构造排序二叉树,然后平衡二叉树
以根结点为初始节点遍历;与当前结点进行比较,如果新增的结点值大,则以当前结点的右子结点作为新的当前结点。否则以当前结点的左子结点作为新的当前结点;循环递归上一步直到找到合适的叶子结点为止;将新增结点与上一步骤中找到的结点进行比对,如果新增结点较大,则添加为右子结点;否则添加为左子结点。
按照上面步骤就可以将一个新增结点添加到排序二叉树中合适的位置
- (1)put方法
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
//如果根节点为null,将传入的键值对构造成根节点(根节点没有父节点,所以传入的父节点为null)
root = new Entry<K,V>(key, value, null);
size = 1;
modCount++;
return null;
}
// 记录比较结果
int cmp;
Entry<K,V> parent;
// 分割比较器和可比较接口的处理
Comparator<? super K> cpr = comparator;
// 有比较器的处理
if (cpr != null) {
// do while实现在root为根节点移动寻找传入键值对需要插入的位置
do {
// 记录将要被掺入新的键值对将要节点(即新节点的父节点)
parent = t;
// 使用比较器比较父节点和插入键值对的key值的大小
cmp = cpr.compare(key, t.key);
// 插入的key较大
if (cmp < 0)
t = t.left;
// 插入的key较小
else if (cmp > 0)
t = t.right;
// key值相等,替换并返回t节点的value(put方法结束)
else
return t.setValue(value);
} while (t != null);
}
// 没有比较器的处理
else {
// key为null抛出NullPointerException异常
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
// 与if中的do while类似,只是比较的方式不同
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
// 没有找到key相同的节点才会有下面的操作
// 根据传入的键值对和找到的“父节点”创建新节点
Entry<K,V> e = new Entry<K,V>(key, value, parent);
// 根据最后一次的判断结果确认新节点是“父节点”的左孩子还是又孩子
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// 对加入新节点的树进行调整
fixAfterInsertion(e);
// 记录size和modCount
size++;
modCount++;
// 因为是插入新节点,所以返回的是null
return null;
}
在put(K key,V value)方法的末尾调用了fixAfterInsertion(Entry<K,V> x)方法,这个方法负责在插入结点后调整树结构和着色,以满足红黑树的要求。
private void fixAfterInsertion(Entry<K,V> x) {
// 插入节点默认为红色
x.color = RED;
// 循环条件是x不为空、不是根节点、父节点的颜色是红色(如果父节点不是红色,则没有连续的红色节点,不再调整)
while (x != null && x != root && x.parent.color == RED) {
// x节点的父节点p(记作p)是其父节点pp(p的父节点,记作pp)的左孩子(pp的左孩子)
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
// 获取pp节点的右孩子r
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
// pp右孩子的颜色是红色(colorOf(Entry e)方法在e为空时返回BLACK),不需要进行旋转操作(因为红黑树不是严格的平衡二叉树)
if (colorOf(y) == RED) {
// 将父节点设置为黑色
setColor(parentOf(x), BLACK);
// y节点,即r设置成黑色
setColor(y, BLACK);
// pp节点设置成红色
setColor(parentOf(parentOf(x)), RED);
// x“移动”到pp节点
x = parentOf(parentOf(x));
} else {//父亲的兄弟是黑色的,这时需要进行旋转操作,根据是“内部”还是“外部”的情况决定是双旋转还是单旋转
// x节点是父节点的右孩子(因为上面已近确认p是pp的左孩子,所以这是一个“内部,左-右”插入的情况,需要进行双旋转处理)
if (x == rightOf(parentOf(x))) {
// x移动到它的父节点
x = parentOf(x);
// 左旋操作
rotateLeft(x);
}
// x的父节点设置成黑色
setColor(parentOf(x), BLACK);
// x的父节点的父节点设置成红色
setColor(parentOf(parentOf(x)), RED);
// 右旋操作
rotateRight(parentOf(parentOf(x)));
}
} else {
// 获取x的父节点(记作p)的父节点(记作pp)的左孩子
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
// y节点是红色的
if (colorOf(y) == RED) {
// x的父节点,即p节点,设置成黑色
setColor(parentOf(x), BLACK);
// y节点设置成黑色
setColor(y, BLACK);
// pp节点设置成红色
setColor(parentOf(parentOf(x)), RED);
// x移动到pp节点
x = parentOf(parentOf(x));
} else {
// x是父节点的左孩子(因为上面已近确认p是pp的右孩子,所以这是一个“内部,右-左”插入的情况,需要进行双旋转处理),
if (x == leftOf(parentOf(x))) {
// x移动到父节点
x = parentOf(x);
// 右旋操作
rotateRight(x);
}
// x的父节点设置成黑色
setColor(parentOf(x), BLACK);
// x的父节点的父节点设置成红色
setColor(parentOf(parentOf(x)), RED);
// 左旋操作
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 根节点为黑色
root.color = BLACK;
}
在这个里面在平衡二叉树时,还有涉及左旋和右旋的操作。
- (2)get方法
public V get(Object key) {
Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
在这个get方法中涉及了getEntry的方法,这个主要是来寻找结点的
final Entry<K,V> getEntry(Object key) {
// 如果有比较器,返回getEntryUsingComparator(Object key)的结果
if (comparator != null)
return getEntryUsingComparator(key);
// 查找的key为null,抛出NullPointerException
if (key == null)
throw new NullPointerException();
// 如果没有比较器,而是实现了可比较接口
Comparable<? super K> k = (Comparable<? super K>) key;
// 获取根节点
Entry<K,V> p = root;
// 对树进行遍历查找节点
while (p != null) {
// 把key和当前节点的key进行比较
int cmp = k.compareTo(p.key);
// key小于当前节点的key
if (cmp < 0)
// p “移动”到左节点上
p = p.left;
// key大于当前节点的key
else if (cmp > 0)
// p “移动”到右节点上
p = p.right;
// key值相等则当前节点就是要找的节点
else
// 返回找到的节点
return p;
}
// 没找到则返回null
return null;
}
- (3)remove方法
真正实现删除结点的是deleteEntry的方法
private void deleteEntry(Entry<K,V> p) {
// 记录树结构的修改次数
modCount++;
// 记录树中节点的个数
size--;
// p有左右两个孩子的情况 标记①
if (p.left != null && p.right != null) {
// 获取继承者节点(有两个孩子的情况下,继承者肯定是右孩子或右孩子的最左子孙)
Entry<K,V> s = successor (p);
// 使用继承者s替换要被删除的节点p,将继承者的key和value复制到p节点,之后将p指向继承者
p.key = s.key;
p.value = s.value;
p = s;
}
// Start fixup at replacement node, if it exists.
// 开始修复被移除节点处的树结构
// 如果p有左孩子,取左孩子,否则取右孩子 标记②
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
// Link replacement to parent
replacement.parent = p.parent;
// p节点没有父节点,即p节点是根节点
if (p.parent == null)
// 将根节点替换为replacement节点
root = replacement;
// p是其父节点的左孩子
else if (p == p.parent.left)
// 将p的父节点的left引用指向replacement
// 这步操作实现了删除p的父节点到p节点的引用
p.parent.left = replacement;
else
// 如果p是其父节点的右孩子,将父节点的right引用指向replacement
p.parent.right = replacement;
// 解除p节点到其左右孩子和父节点的引用
p.left = p.right = p.parent = null;
if (p.color == BLACK)
// 在删除节点后修复红黑树的颜色分配
fixAfterDeletion(replacement);
} else if (p.parent == null) {
/* 进入这块代码则说明p节点就是根节点(这块比较难理解,如果标记①处p有左右孩子,则找到的继承节点s是p的一个祖先节点或右孩子或右孩子的最左子孙节点,他们要么有孩子节点,要么有父节点,所以如果进入这块代码,则说明标记①除的p节点没有左右两个孩子。没有左右孩子,则有没有孩子、有一个右孩子、有一个左孩子三种情况,三种情况中只有没有孩子的情况会使标记②的if判断不通过,所以p节点只能是没有孩子,加上这里的判断,p没有父节点,所以p是一个独立节点,也是树种的唯一节点……有点难理解,只能解释到这里了,读者只能结合注释慢慢体会了),所以将根节点设置为null即实现了对该节点的删除 */
root = null;
} else { /* 标记②的if判断没有通过说明被删除节点没有孩子,或它有两个孩子但它的继承者没有孩子。如果是被删除节点没有孩子,说明p是个叶子节点,则不需要找继承者,直接删除该节点。如果是有两个孩子,那么继承者肯定是右孩子或右孩子的最左子孙 */
if (p.color == BLACK)
// 调整树结构
fixAfterDeletion(p);
// 这个判断也一定会通过,因为p.parent如果不是null则在上面的else if块中已经被处理
if (p.parent != null) {
// p是一个左孩子
if (p == p.parent.left)
// 删除父节点对p的引用
p.parent.left = null;
else if (p == p.parent.right)// p是一个右孩子
// 删除父节点对p的引用
p.parent.right = null;
// 删除p节点对父节点的引用
p.parent = null;
}
}
}
- HashMap
- HashMap的构造方法
//1.构造一个带指定初始容量和加载因子的空HashMap
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
//2.构造一个带指定初始容量和默认加载因子(0.75)的空 HashMap
public HashMap(int initialCapacity)
{
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
//3.构造一个具有默认初始容量 (16)和默认加载因子 (0.75)的空 HashMap
public HashMap()
{
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
//4.构造一个映射关系与指定 Map相同的新 HashMap
public HashMap(Map<? extends K, ? extends V> m)
{
this.loadFactor = DEFAULT_LOAD_FACTOR;
putMapEntries(m, false);
}
- (1)put方法
public V put(K key, V value)
{
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict)
{
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)//该key的hash值对应的那个节点为空
tab[i] = newNode(hash, key, value, null);//新建节点
else
{
//节点不为空,先比较链表上的第一个节点
Node<K,V> e; K k;
if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount)
{
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) //若该key对应的键值对已经存在,则用新的value取代旧的value
{
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
// 若“该key”对应的键值对不存在,则将“key-value”添加到table中
++modCount;
//如果加入该键值对后超过最大阀值,则进行resize操作
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
- (2)get方法
public V get(Object key) {
Node<K,V> e;
//传入key的hash
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
//这里访问(n - 1) & hash其实就是jdk1.7中indexFor方法的作用
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
//判断桶索引位置的节点是不是相同(通过hash和equals判断),如果相同返回此节点
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
//判断是否是红黑树节点,如果是查找红黑树
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
//如果是链表,遍历链表
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
//如果不存在返回null
return null;
}
3. 实验过程中遇到的问题和解决过程
-
问题1:实验三的那个决策树,我最开始完全不知道要干嘛,后面的数字我也有点懵
-
问题1解决方案:我进行了几次实验,重复的利用Y、N来看看都对应什么,后来发现,后面的数字其实就是将之前的各个句子当做数字,然后一个个形成树,后来我试图再添加一个树,我就添加到了那串数字的最后,但是会有问题,有时会出现BUG
-
问题1后续解决方案:后来我在想,是不是那个数字是有规律的,我就继续找,后来才知道,其实顺序是从树的左下到右下,再向上到头的
-
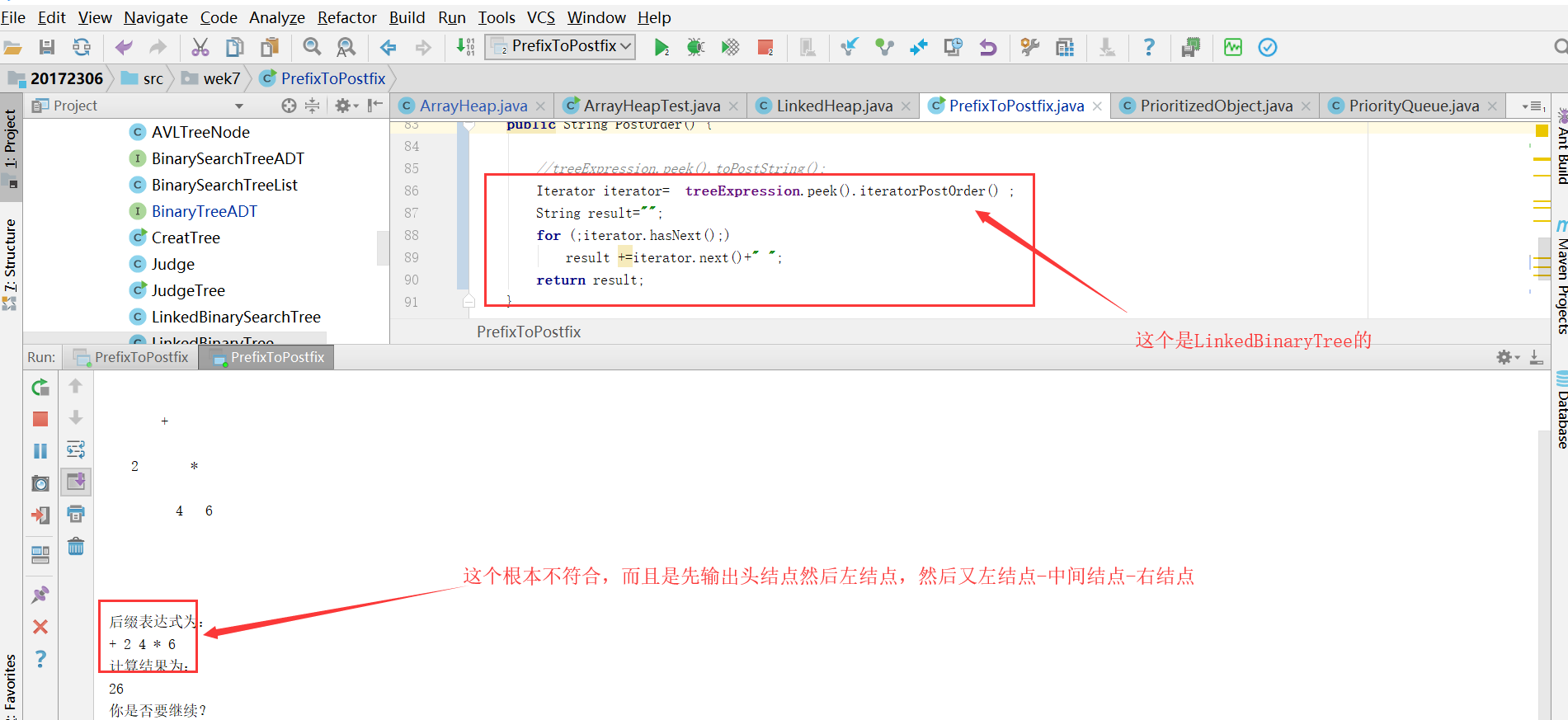
问题2:在做实验四的时候,我最开始的toString我用的是利用我之前的LinkedBinaryTree的后序的迭代器进行编写的,但是总是出现这样的问题,它出现的不是后序的输出
![]()
-
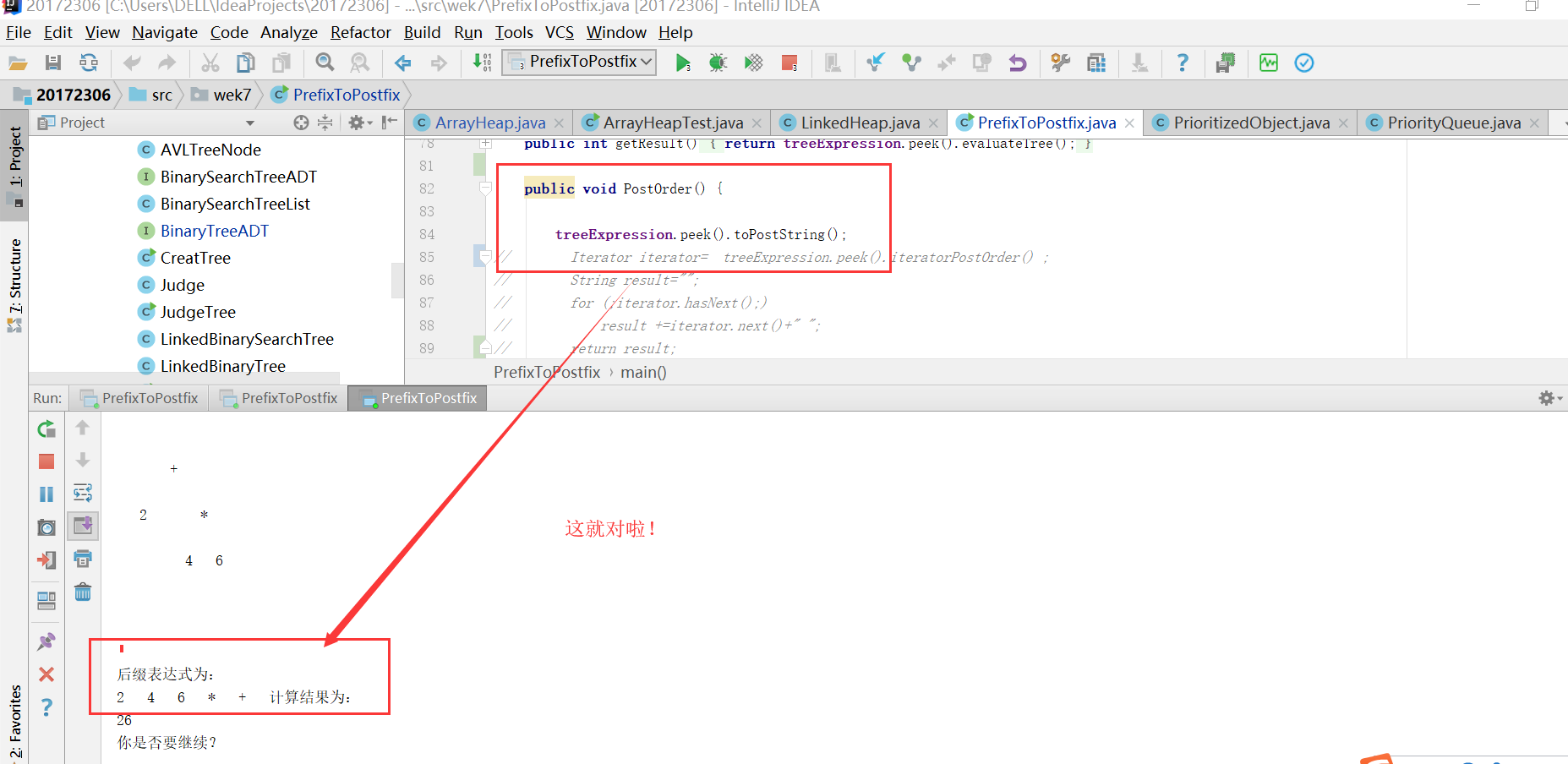
问题2解决方案:我一开始以为是不是我的LinkedBinaryTree的那段代码有问题,我想到之前测试过,我就又测试一遍,发现是没问题的;之后,我试图看其他人关于LinkedBinaryTree的代码,发现跟我的一样啊,因为这个其实每个人都是基本一样的;我后来又想,是不是不是我的toString有问题呢,我就单步调试了一下,发现就是这个问题;我最后尝试将IDEA关掉重进,结果亦如此,主要是我跟别人的一样啊问题出在哪呢??我很疑惑,而且依旧疑惑,问了仇夏和结对伙伴,依旧没有结果。后来我换了一个toString,我调用了toPostring方法,是我LinkedBinaryTree的输出后序的方法,结果就成功了。
![]()
-
问题3:其实最开始做中序先序表达树的时候吧,我有点蒙圈,我不知道怎么做
-
问题3解决方案:很幸运,谭鑫不厌其烦,我问他,他就给我讲了,其实就是先序的第一个为root,然后在中序中找root,把它分成两部分,再在这两部分中的先序继续找小树中的root,在中序中继续分两部分,以此向下。主要总结就是:先序是来找root,中序是来分块的。然后其实代码就很好写啦!
其他(感悟、思考等)
我觉得实验三的那个决策树,特别好玩,我可以用这个来测试我想测试的东西,还挺好玩的,头回觉得会Java是一件很好的事情,如果我不会树的话,我就没法把问题弄出来了;实验四我觉得特别难,其实都是在理解其他人的代码的情况下渐渐写出来的;实验六嘛,嗯~我觉得那个红黑树的源代码实在很长,很难懂,很难,很难懂!!!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号