归并排序算法Java实现

2017-11-30 18:27 lc_java 阅读(440) 评论(0) 编辑收藏举报

一. 算法描述

归并排序采用了分治策略（divide-and-conquer），就是将原问题分解为一些规模较小的相似子问题，然后递归解决这些子问题，最后合并其结果作为原问题的解。

归并排序将待排序数组A[1..n]分成两个各含n/2个元素的子序列，然后对这个两个子序列进行递归排序，最后将这两个已排序的子序列进行合并，即得到最终排好序的序列。具体排序过程如下图所示：

归并排序中一个很重要的部分是两个已排序序列合并的过程，这里需要另外开辟一块新的空间来作为存储这两个已排序序列的临时容器。假设对A[p..r]序列进行合并，已知A[p..q]及A[q+1..r]为已排序的序列，合并的具体步骤为：

Step 1：新建两个数组L、R分别存储待合并序列A[p..q]和A[q+1..r]，将待排序序列中的对应元素copy到L和R中，L和R最后设置一个极大值作为“哨兵”；

Step 2：令指针i指向L的起始元素，j指向R的起始元素，k指向A待合并部分的起始元素A[p]；

Step 3：若L[i]≤R[j]，令A[k]=L[i]，i=i+1，k=k+1；

否则，令A[k]=R[j]，j=j+1，k=k+1；

（这一步即依次比较i、j所指向的元素，将较小值依次放入到A中相应位置。）

Step 4 ：重复Step 3，r-p+1次后停止，即依次确定A[p..q]每个位置上的元素。

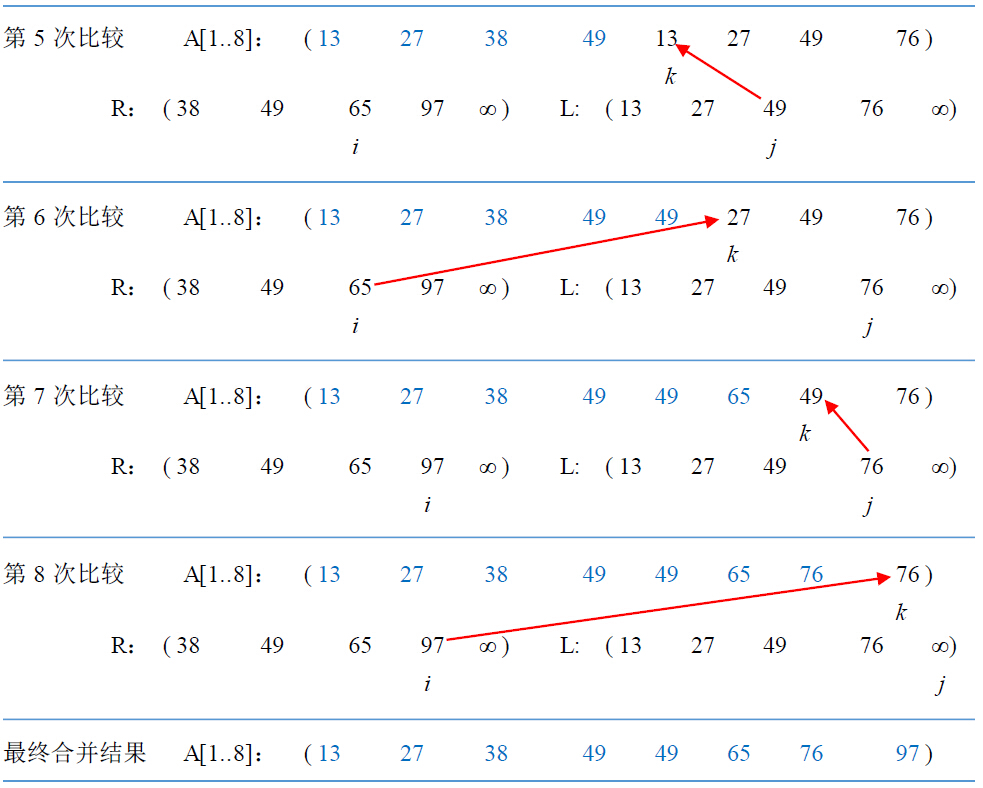
经过合并操作后，A[p..q]为一个有序序列。若待合并序列为（38， 49， 65， 97， 13， 27， 49， 76），p=1，q=4,， r=8，即A[1..4]和A[5..8]分别为有序序列，则合并操作的具体过程如下图所示：

package com.neuedu.algorithm;
 
import java.util.Arrays;
 
public class MergeSort {
//归并排序
    /*归并排序采用递归实现
     * 分阶段可以理解为就是递归拆分子序列的过程、
     * 治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，
     * */
    public static void main(String []args){
        int []arr = {9,8,7,6,5,4,3,2,1};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void sort(int []arr){
        int []temp = new int[arr.length];//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        sort(arr,0,arr.length-1,temp);
    }
    private static void sort(int[] arr,int left,int right,int []temp){
        if(left<right){
            int mid = (left+right)/2;
            sort(arr,left,mid,temp);//左边归并排序，使得左子序列有序
            sort(arr,mid+1,right,temp);//右边归并排序，使得右子序列有序
            merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
        }
    }
    private static void merge(int[] arr,int left,int mid,int right,int[] temp){
        int i = left;//左序列指针
        int j = mid+1;//右序列指针
        int t = 0;//临时数组指针
        while (i<=mid && j<=right){
            if(arr[i]<=arr[j]){
                temp[t++] = arr[i++];
            }else {
                temp[t++] = arr[j++];
            }
        }
        while(i<=mid){//将左边剩余元素填充进temp中
            temp[t++] = arr[i++];
        }
        while(j<=right){//将右序列剩余元素填充进temp中
            temp[t++] = arr[j++];
        }
        t = 0;
        //将temp中的元素全部拷贝到原数组中
        while(left <= right){
            arr[left++] = temp[t++];
        }
    }
 
}