向量与三角

[题目]
如图，等边 \(△ABC\) 的边长为 \(2\) ，顶点 \(B,C\) 分别在 \(x\) 轴的非负半轴，\(y\) 轴的非负半轴上滑动，\(M\) 为 \(AB\) 中点，则 \(\overrightarrow{OA}\cdot\overrightarrow{OM}\) 的最大值为 \((\qquad)\)

\(A.\sqrt{7}\qquad\qquad B.\dfrac{5}{2}+\sqrt{7}\qquad\qquad C. \dfrac{7}{2}\qquad\qquad D. 3+\dfrac{3\sqrt{3}}{2}\)

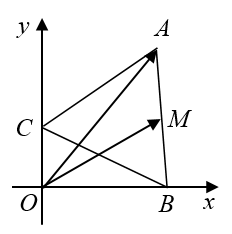
**[解析]** 如图，设 $\angle OBC=\theta ,\theta\in[0,\dfrac{\pi}{2}]$ ， 则 $OB=2\cos\theta,OC=2\sin\theta$ .所以$$\begin{array}{clr}\overrightarrow{OA}\cdot\overrightarrow{OM}&=(\overrightarrow{OC}+\overrightarrow{CA})\cdot(\overrightarrow{OB}+\overrightarrow{BM}) \\ &=\overrightarrow{OC}\cdot\overrightarrow{OB}+\overrightarrow{CA}\cdot\overrightarrow{OB}+\overrightarrow{OC}\cdot\overrightarrow{BM}+\overrightarrow{CA}\cdot\overrightarrow{BM}\end{array}$$代入数据得$$\overrightarrow{OA}\cdot\overrightarrow{OM}=0+2\cdot2\cos\theta\cdot\cos(\dfrac{\pi}{3}-\theta)+2\sin\theta\cdot1\cdot\cos(\dfrac{\pi}{6}-\theta)+2\cdot1\cdot\cos\dfrac{\pi}{3}$$化简得$$\overrightarrow{OA}\cdot\overrightarrow{OM}=\sqrt{7}\sin(2\theta+\varphi)+\dfrac{5}{2}$$所以 $\overrightarrow{OA}\cdot\overrightarrow{OM}$ 的最大值为 $\dfrac{5}{2}+\sqrt{7}$.