四点共圆

第一题

如图，在四边形 \(ABCD\) 中，\(\angle ABC=\angle ADC=90^{\circ}\)，\(\angle BCD=120^{\circ}\) ，\(AB=4,AD=5\)，则 \(AC=(\qquad)\)

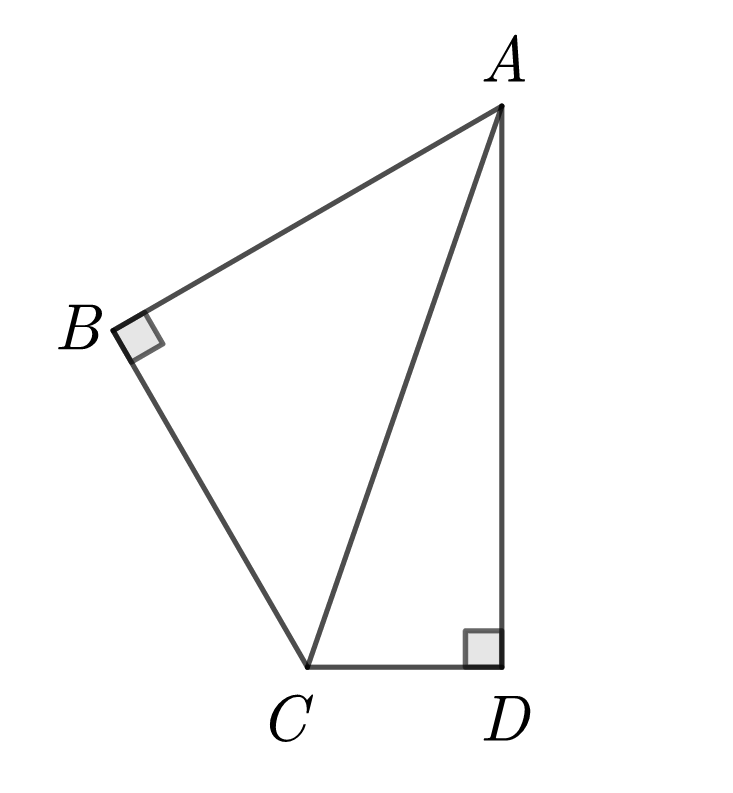
A. \(\dfrac{\sqrt{21}}{2}\)

B. \(\sqrt{21}\)

C. \(\sqrt7\)

D. \(2\sqrt7\)

解析：

因为

\[BD^2=AB^2+AD^2-2AB\cdot AD\cdot\cos\angle BAD=21 \]

所以 \(BD=\sqrt{21}\) ，由题意知 \(A,B,C,D\) 四点共圆，所以

\[\dfrac{BD}{\sin 60^{\circ}}=2R=AD \]

所以 \(AD=2\sqrt7\) .

第二题

已知圆 \(C:x^2+(y-2)^2=1\) ，圆 \(C\) 外一点 \(P(2,0)\) ，过点 \(P\) 作圆 \(C\) 的两条切线 \(PA,PB\) ，切点为 \(A,B\) ，在直线 \(AB\) 的方程为 \(\underline{\qquad\qquad}\).

解析：

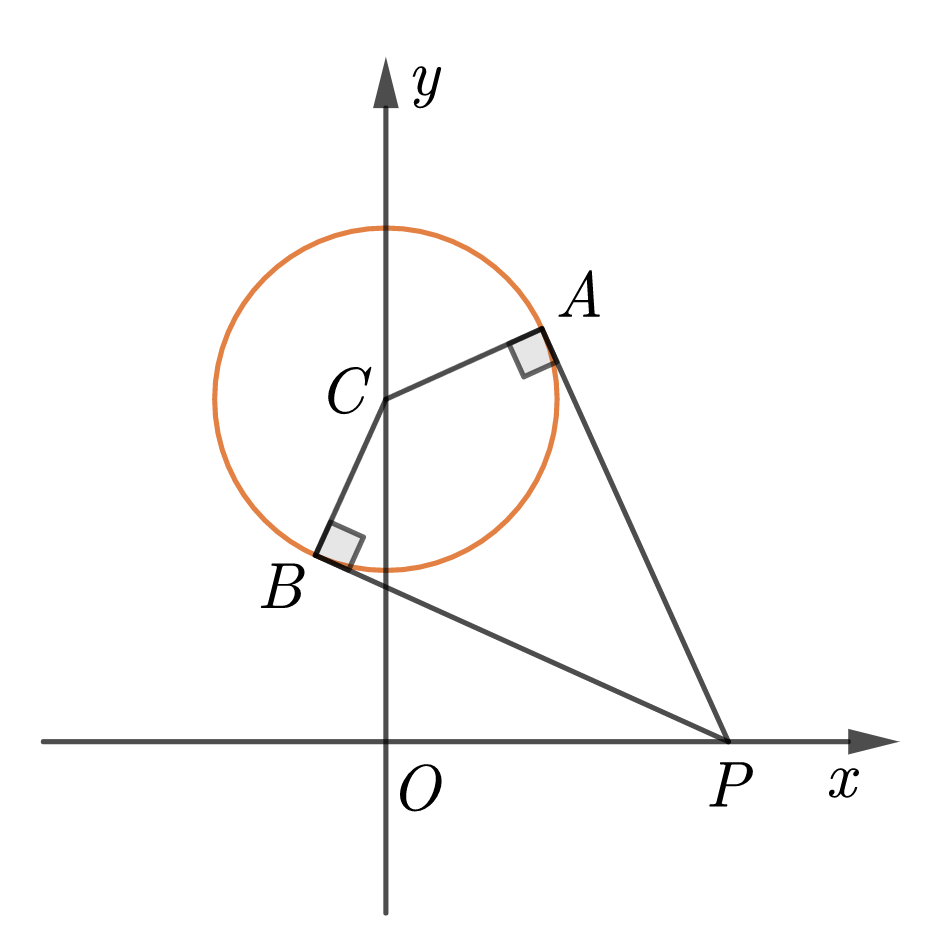
如图，由题意知 \(P,A,B,C\) 四点共圆，设圆心为 \(M\) ，因为 \(C(0,2)\) ，则

\[M(1,1) , r^2=2 \]

所以圆 \(M\) 的方程为

\[(x-1)^2+(y-1)^2=2 \]

两圆方程相减得直线 \(AB\) 方程为

\[2x-2y+3=0 \]