一道立体几何大题求体积问题
题目:
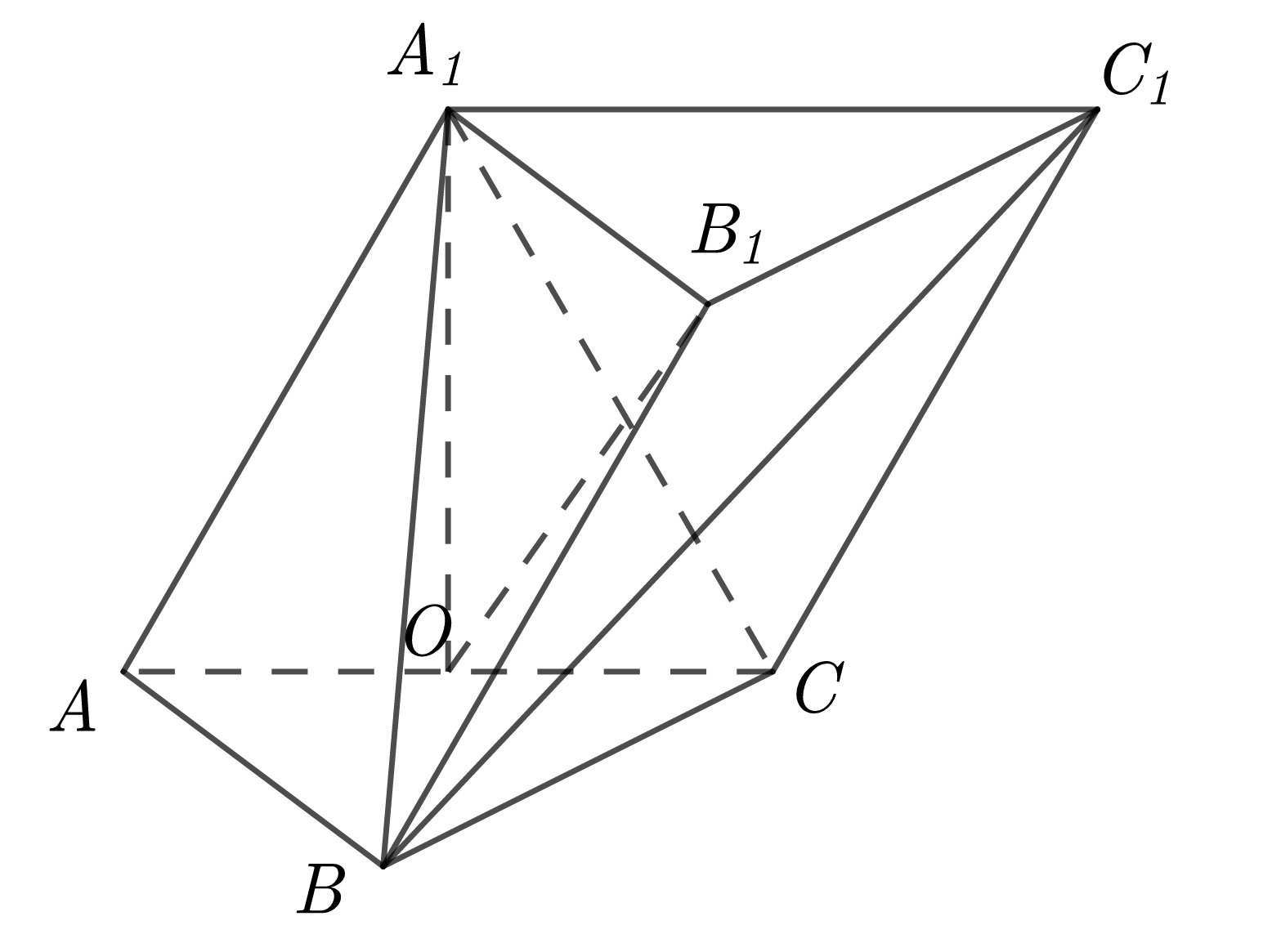
如图,在三棱柱 \(ABC-A_1B_1C_1\) 中,侧面 \(AA_1C_1C\perp\) 底面 \(ABC\) ,\(AA_1=A_1C=AC=2\) ,\(AB=BC\) ,且 \(AB\perp BC\) ,\(O\) 为 \(AC\) 的中点.
(1) 求证:平面 \(A_1B_1O\perp\) 平面 \(BCA_1\) ;
(2) 若点 \(E\) 在 \(BC_1\) 上 ,且 \(OE//\) 平面 \(A_1AB\) ,求三棱锥 \(E-A_1BC\) 的体积.
解析:
(1) 因为三角形 \(AA_1C\) 为等边三角形,所以 \(A_1O\perp AC\),因为侧面 \(AA_1C_1C\perp\) 底面 \(ABC\),且面 \(AA_1C_1C\;\cap\) 底面 \(ABC=AC\),所以 \(A_1O\perp\) 平面 \(ABC\),所以 \(A_1O\perp BC\) . 又因为 \(BC\perp AB,AB//A_1B_1\) ,所以 \(BC\perp A_1B_1\) . 而 \(A_1O\;\cap A_1B_1=A_1\),所以 \(BC\perp\) 平面 \(A_1B_1O\) ,因为 \(BC\subset\) 平面 \(BCA_1\) ,所以平面 \(BCA_1//\) 平面 \(A_1B_1O\) .
(2) 如图,连接 \(AB_1\) ,\(OE\) .
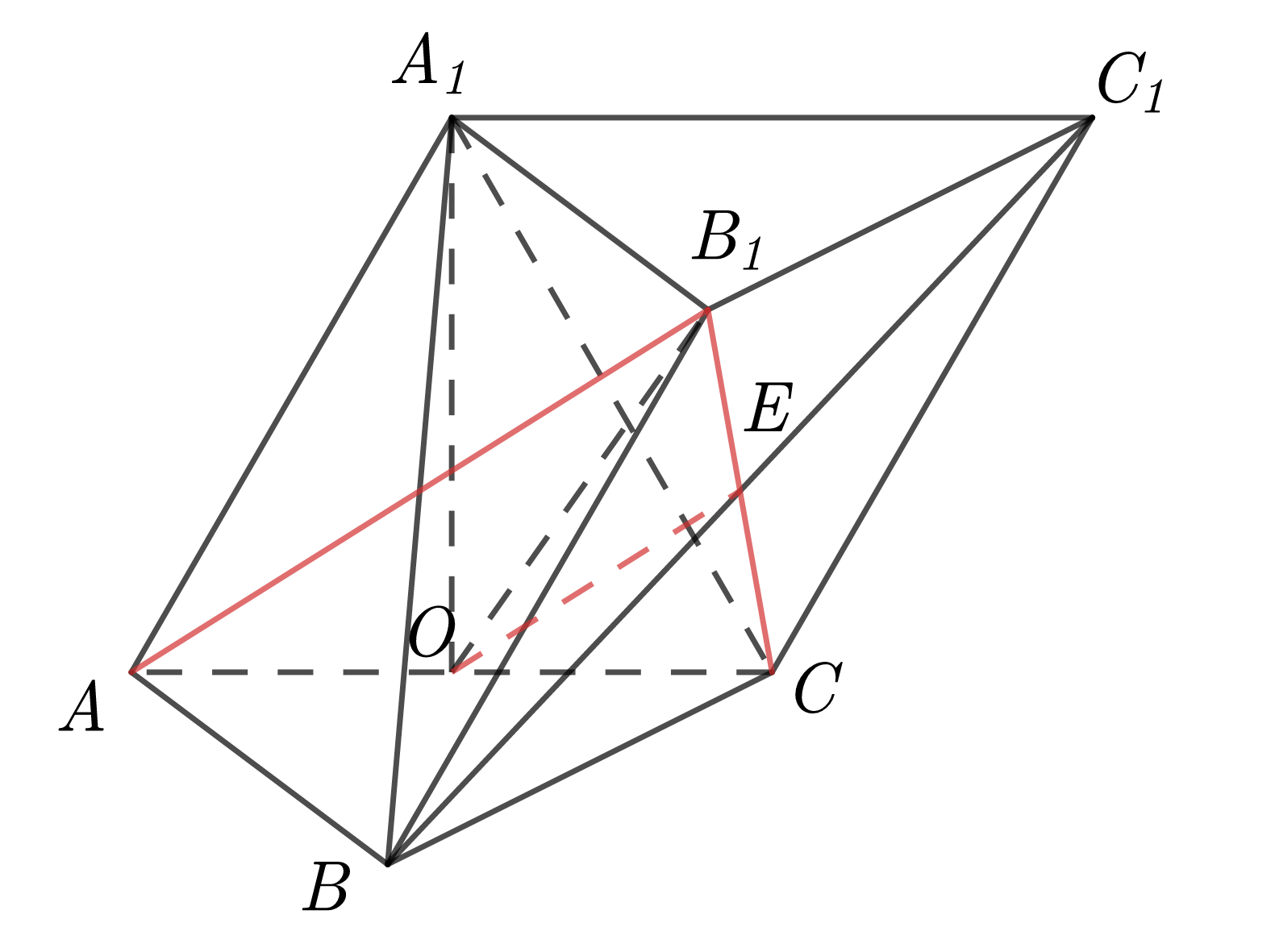
因为 \(OE//\) 平面 \(A_1ABB_1\),\(OE\subset\) 平面 \(AB_1C\) ,平面 \(AB_1C\;\cap\) 平面 \(A_1ABB_1=AB_1\) ,所以 \(OE//AB_1\) . 又因为 \(O\) 为 \(AC\) 中点,所以 \(E\) 为 \(B_1C\) 的中点,也即 \(BC_1\) 与 \(B_1C\) 的交点。
方法一:
所以
方法二:
如图,以 \(O\) 为原点建立空间直角坐标系,则
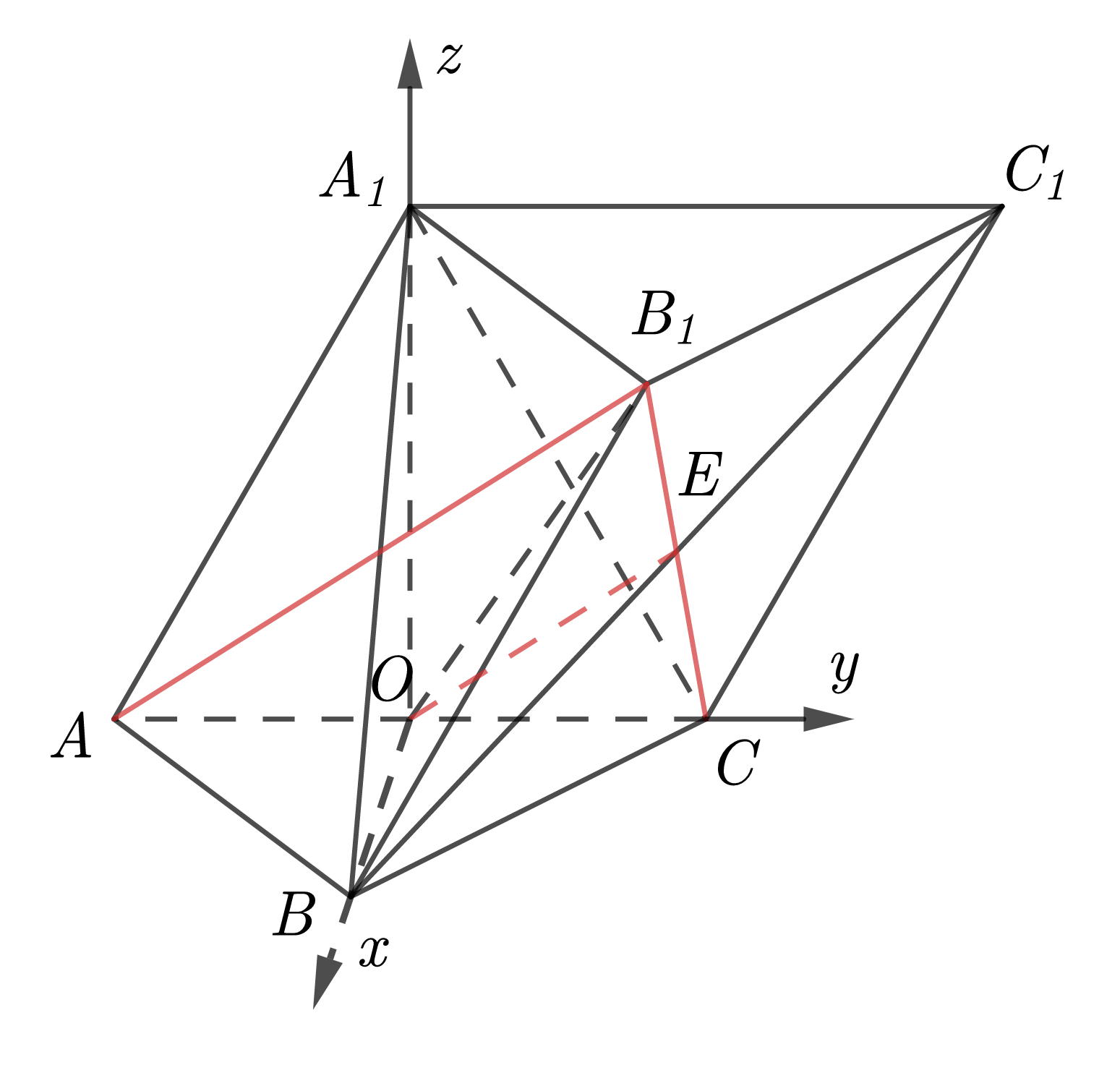
\(A_1(0,0,\sqrt3),B(1,0,0),C(0,1,0),C_1(0,2,\sqrt3),E\Big(\dfrac12,1,\dfrac{\sqrt3}{2}\Big)\) ,故有 \(\overrightarrow{A_1B}=(1,0,-\sqrt3),\overrightarrow{A_1C}=(0,1,-\sqrt3),\overrightarrow{BE}=\Big(-\dfrac12,1,\dfrac{\sqrt3}2\Big)\) ,设 \(\overrightarrow{n}=(x,y,z)\) 为平面 \(A_1BC\) 的法向量,则
令 \(x=\sqrt3\) ,则 \(\overrightarrow{n}=(\sqrt3,\sqrt3,1)\),则点 \(E\) 到平面 \(A_1BC\) 的距离
又在等腰三角形 \(ABC\) 中,\(S_{\triangle A_1BC}=\dfrac{\sqrt7}{2}\) ,所以

