异面直线最小距离

如图，在正方体 \(ABCD-A_1B_1C_1D_1\) 中，\(M,N\) 分别是棱 \(AB,BB_1\) 的中点，点 \(P\) 在对角线 \(CA_1\) 上运动. 当 \(\triangle PMN\) 的面积最小时，点 \(P\) 的位置是 \((\qquad)\)

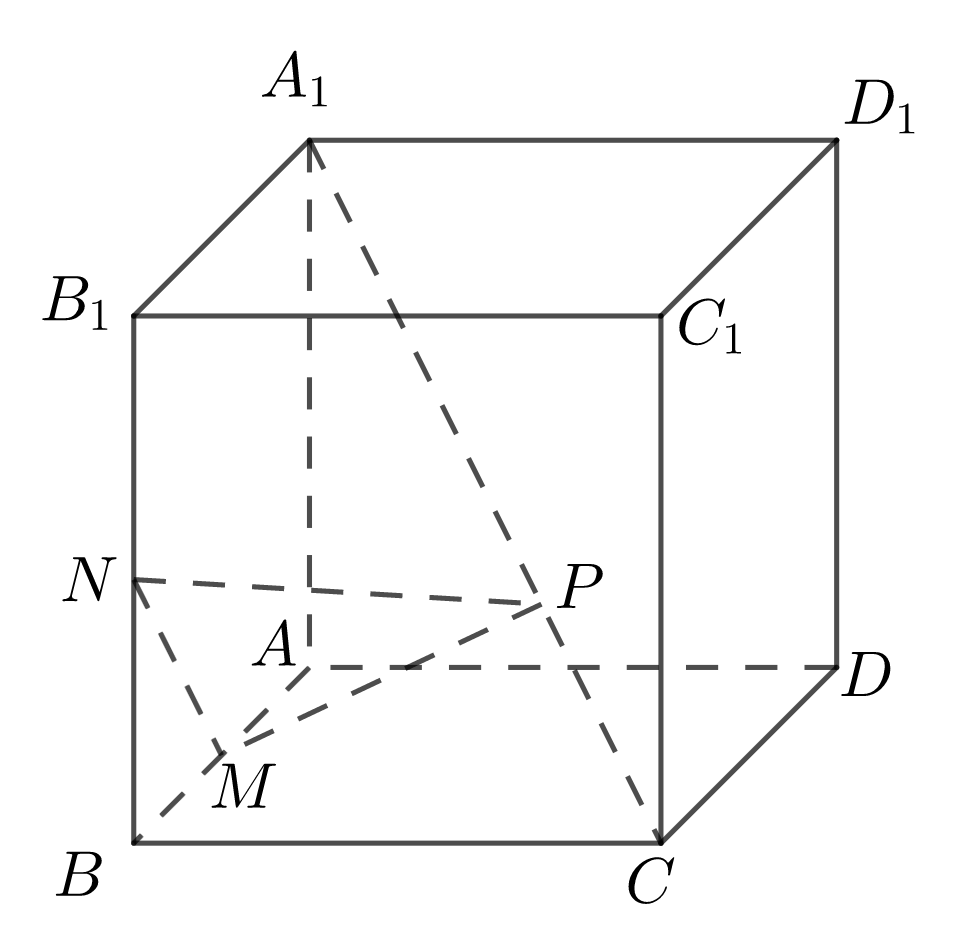
A. 线段 \(CA_1\) 的三等分点，且靠近 \(A_1\)

B. 线段 \(CA_1\) 的中点

C. 线段 \(CA_1\) 的三等分点，且靠近点 \(C\)

D. 线段 \(CA_1\) 的四等分点，且靠近点 \(C\)

解析：

要使 \(\triangle PMN\) 的面积最小，则需点 \(P\) 到直线 \(MN\) 的距离最小，即求异面直线 \(MN\) 与 \(A_1C\) 的最小距离。如图

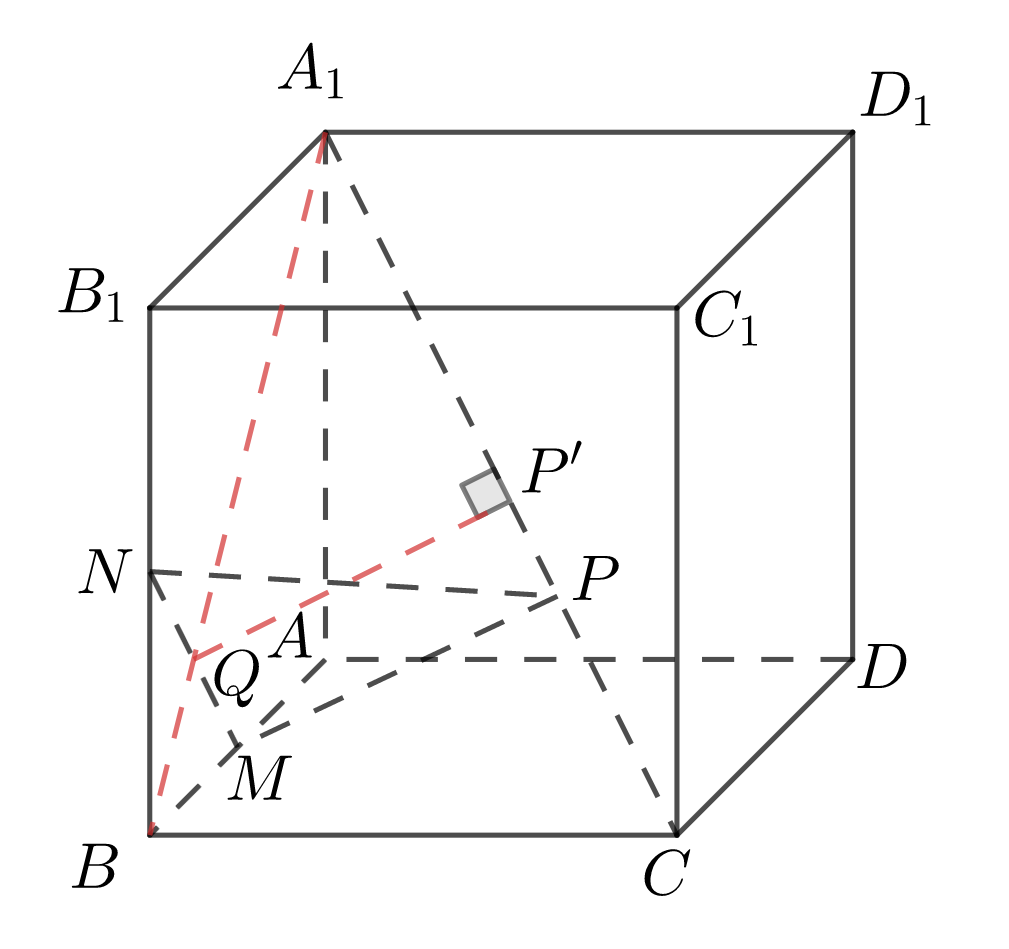
连接 \(A_1B\) 交 \(MN\) 于点 \(Q\) ，过点 \(Q\) 作 \(QP'\perp A_1C\) ，交 \(A_1C\) 于点 \(P'\) ，因为 \(MN\perp A_1B\) ，\(MN\perp BC\) ，所以 \(MN\perp\) 平面 \(A_1BC\) ，所以 \(MN\perp QP'\) ，又 \(QP'\perp A_1C\) ，所以 \(|QP'|\) 为异面直线 \(MN,A_1C\) 之间的最小距离。设正方体棱长为 \(1\) ，求得

\[A_1B=\sqrt{2},A_1Q=\dfrac{3}{4}\sqrt{2},A_1C=\sqrt{3} \]

易知 \(\triangle A_1QP'\sim\triangle A_1CB\) ，设 \(|A_1P'|=x\) ，则

\[\dfrac{|A_1P'|}{|A_1B|}=\dfrac{|A_1Q|}{|A_1C|}\Longrightarrow \dfrac{x}{\sqrt{2}}=\dfrac{\dfrac{3}{4}\sqrt2}{\sqrt3} \]

解得 \(x=\dfrac{\sqrt3}{2}\) ，所以当点 \(P\) 在点 \(P'\) 处（即 \(A_1C\) 中点）时，\(\triangle PMN\) 的面积最小.

答案：B