阿基米德三角形

已知抛物线 \(C:x^2=2py\) ，弦 \(AB\) 过 \(C\) 的焦点 \(F\) ，过 \(A,B\) 两点作抛物线 \(C\) 的两条切线，若两切线相交于点 \(P\) ，则

(1) \(AP\perp PB\) ；

(2) 点 \(P\) 在抛物线 \(C\) 的准线上。

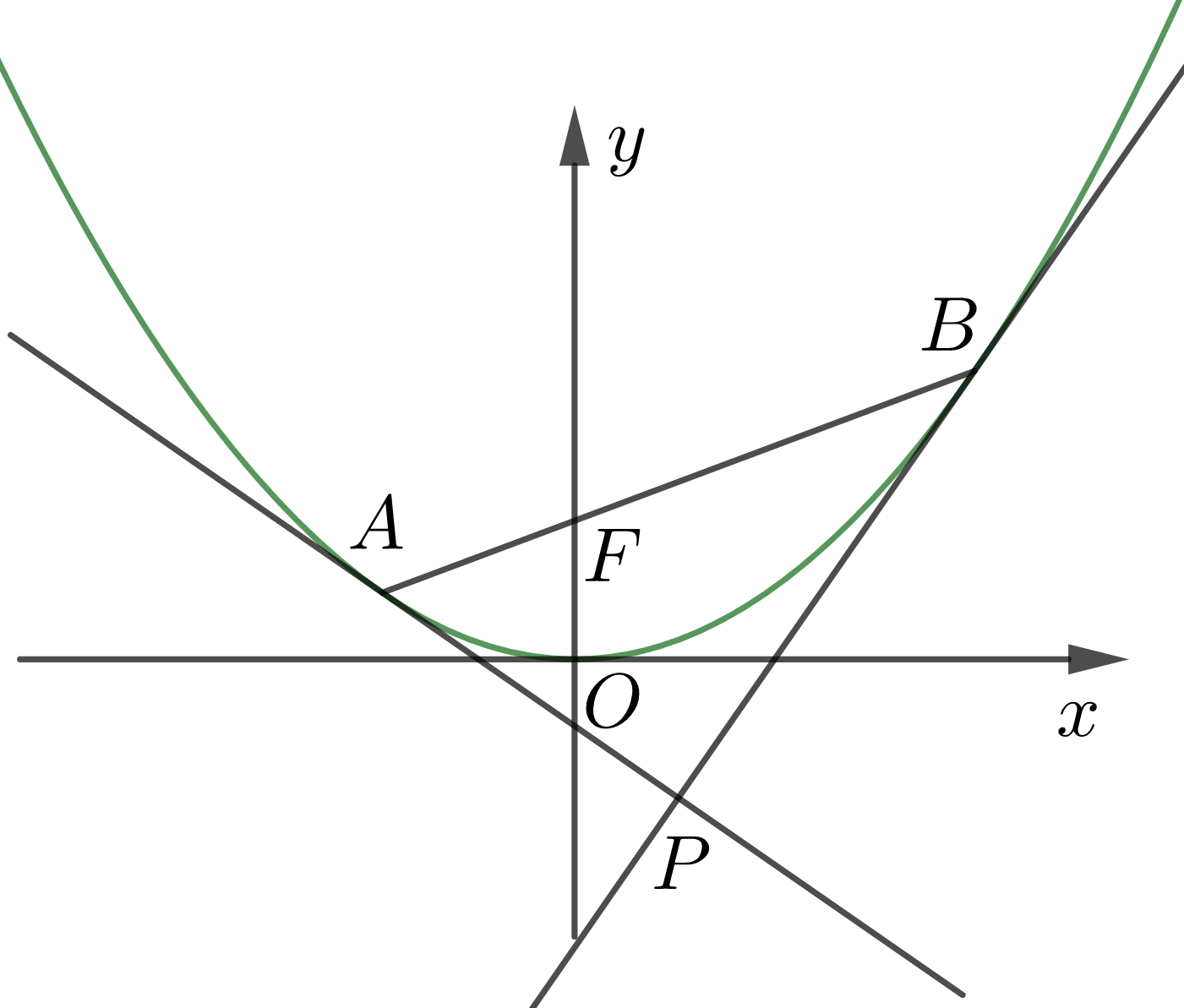
证明：设 \(A\Big(x_1,\dfrac{x_1^2}{2p}\Big),B\Big(x_2,\dfrac{x_2^2}{2p}\Big),P(x_0,y_0)\) ，设过点 \(P\) 的切线斜率为 \(k\) ，则切线方程为 \(y=y_0+k(x-x_0)\) ，联立抛物线方程得

\[x^2-2pkx+2pkx_0-2py_0=0 \]

令 \(\Delta=0\) 得

\[4p^2k^2-8px_0k+8py_0=0 \]

故

\[k_1+k_2=\dfrac{2x_0}{p},k_1k_2=\dfrac{2y_0}{p} \]

所以

\[x=\dfrac{2pk\pm\sqrt{\Delta}}{2}=pk\;\Longrightarrow\;x_1=pk_1,x_2=pk_2 \]

则 \(A\Big(pk_1,\dfrac{pk_1^2}{2}\Big), B\Big(pk_2,\dfrac{pk_2^2}{2}\Big)\)，由 \(A,F,B\) 三点共线得 \(k_{AF}=k_{FB}\) ，即

\[\dfrac{\dfrac{pk_1^2}{2}-\dfrac p2}{pk_1}=\dfrac{\dfrac{pk_2^2}{2}-\dfrac p2}{pk_2} \]

化简得

\[\dfrac{(k_1k_2+1)(k_1-k_2)}{k_1k_2}=0 \]

因为 \(k_1\neq k_2\) ，所以 \(k_1k_2=-1\) , 所以 \(AP\perp PB\) .

又 \(k_1k_2=\dfrac{2y_0}{p}=-1\) ，所以 \(y_0=-\dfrac{p}{2}\) . 所以点 \(P\) 在抛物线的准线上。