2020年高考数学全国1卷圆锥曲线

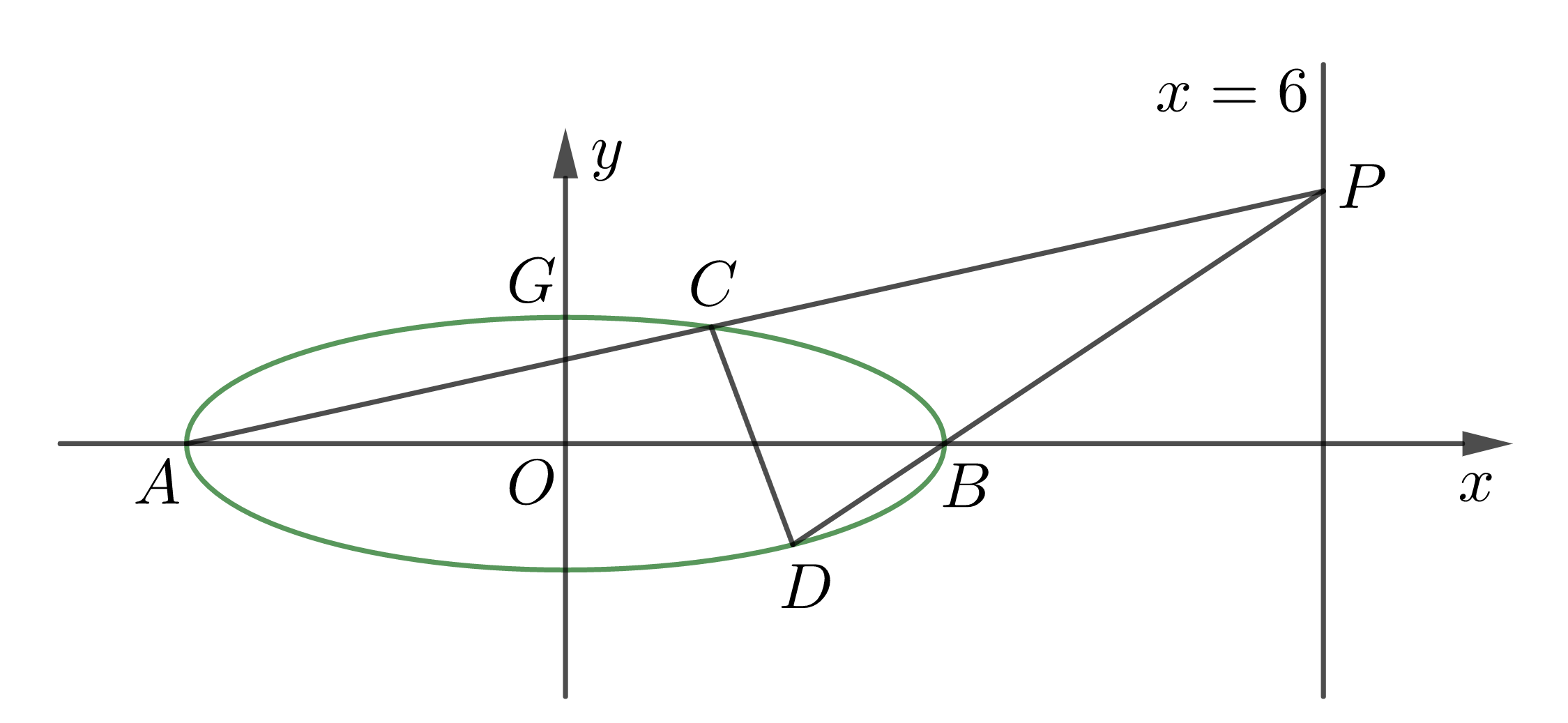
已知 \(A,B\) 分别为椭圆 \(E:\dfrac{x^2}{a^2}+y^2=1(a>0)\) 的左、右顶点，\(G\) 为 \(E\) 的上顶点，\(\overrightarrow{AG}\cdot\overrightarrow{GB}=8\) ，\(P\) 为直线 \(x=6\) 上的动点，\(PA\) 与 \(E\) 的另一交点为 \(C\) ，\(PB\) 与 \(E\) 的另一交点为 \(D\) .

(1) 求 \(E\) 的方程；

(2) 证明：直线 \(CD\) 过定点.

解析：

(1) \(\dfrac{x^2}{9}+y^2=1\)

(2) 设 \(C(x_1,y_1),D(x_2,y_2)\) ，则有

\[l_{AC}:y=\dfrac{y_1}{x_1+3}(x+3)\;\;,\;\;l_{BD}:y=\dfrac{y_2}{x_2-3}(x-3) \]

因为直线 \(AC,BD\) 交于直线 \(x=6\) 上同一点，则

\[\begin{align}\dfrac{9y_1}{x_1+3}=\dfrac{3y_2}{x_2-3}\end{align} \]

情形一 当直线 \(CD\) 斜率存在时，设直线 \(CD\) 的方程为 \(y=kx+m\) ，联立

\[\begin{cases}y=kx+m\\x^2+9y^2=9\end{cases}\Longrightarrow(1+9k^2)x^2+18kmx+9m^2-9=0 \]

则 \(x_1+x_2=-\dfrac{18km}{1+9k^2},x_1x_2=\dfrac{9m^2-9}{1+9k^2}\) ，将 \((1)\) 式两边平方得

\[\begin{align}\dfrac{9\cdot9y_1^2}{(x_1+3)^2}=\dfrac{9y_2^2}{(x_2-3)^2}\end{align} \]

因为 \(C,D\) 在椭圆 \(E\) 上，则

\[9y_1^2=9-x_1^2\;,\;9y_2^2=9-x_2^2 \]

代入 \((2)\) 式，得

\[\dfrac{9\cdot(9-x_1^2)}{(x_1+3)^2}=\dfrac{9-x_2^2}{(x_2-3)^2} \]

化简得

\[4x_1x_2-15(x_1+x_2)+36=0 \]

则

\[4\cdot\dfrac{9m^2-9}{1+9k^2}+15\cdot\dfrac{18km}{1+9k^2}+36=0 \]

化简得

\[2m^2+15km+18k^2=(2m+3k)(m+6k)=0 \]

解得 \(m=-\dfrac{3}{2}k\) 或 \(m=-6k\) (舍) ，则直线 \(CD\) 为 \(y=k\Big(x-\dfrac32\Big)\) ，过定点 \(\Big(\dfrac32,0\Big)\) .

情形二 当直线 \(CD\) 的斜率不存在时，设为 \(x=m\) ，则此时 \(x_1=x_2=m,y_1=-y_2\) ，代入 \((1)\) 式求得 \(m=\dfrac{3}{2}\) ，过点 \(\Big(\dfrac32,0\Big)\)

综上，直线 \(CD\) 过定点 \(\Big(\dfrac32,0\Big)\) .