二维均值不等式的几何证明

对于任意正实数 \(a,b\) ，有

\[\sqrt{\dfrac{a^2+b^2}{2}}\geqslant\dfrac{a+b}{2}\geqslant\sqrt{ab}\geqslant\dfrac{2}{\dfrac1a+\dfrac1b} \]

当且仅当 \(a=b\) 时，等号成立.

1、\(\sqrt{\dfrac{a^2+b^2}{2}}\geqslant\dfrac{a+b}{2}\)

如图，点 \(D\) 在半圆 \(O\) 上，点 \(C\) 在直径 \(AB\) 上，且 \(OD\perp AB\) ，设 \(AC=a,BC=b\) .

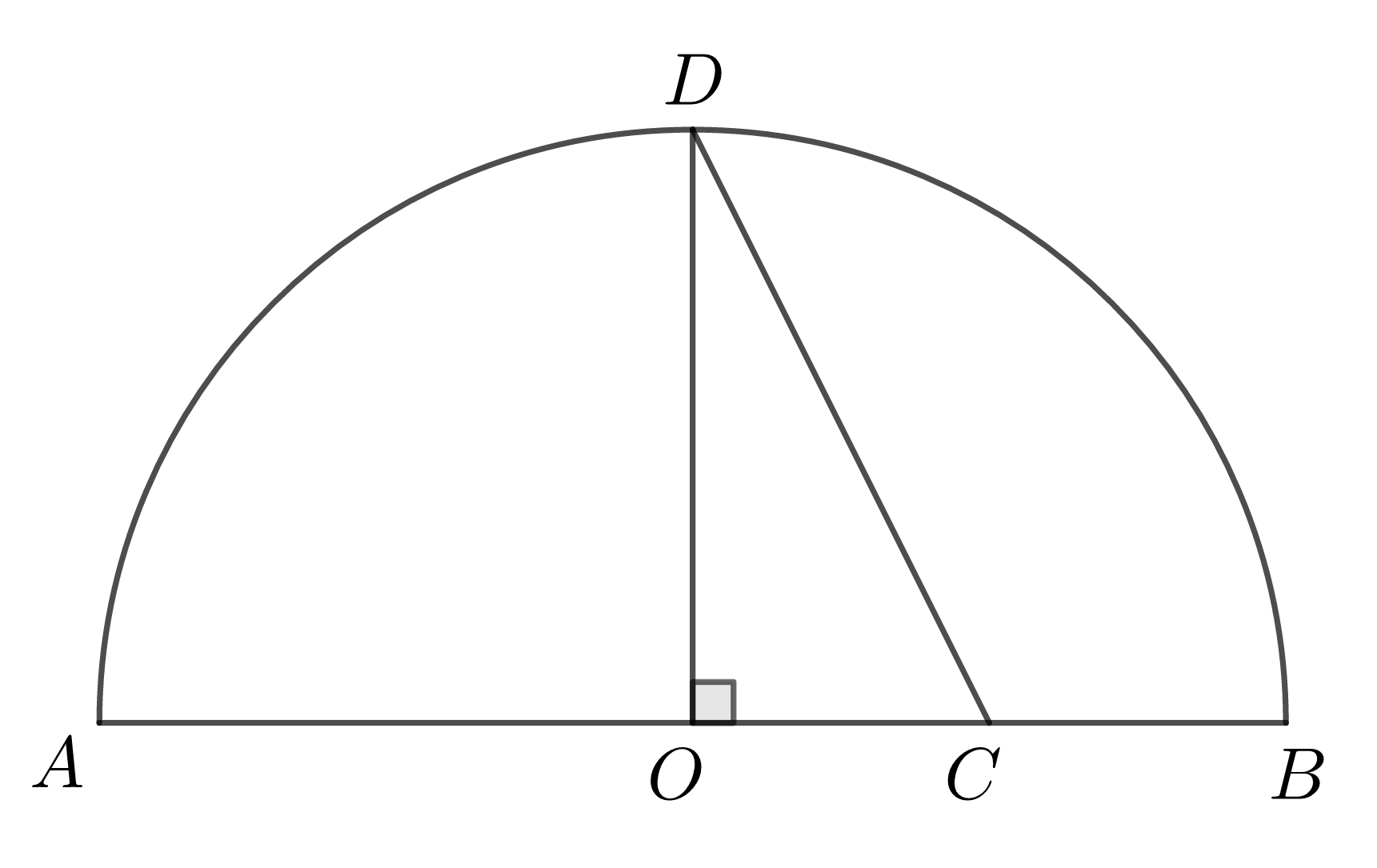
证明：因为 \(AC=a,BC=b\)，则

\[OD=\dfrac{a+b}{2}\;\;,\;\;OC=\dfrac{a-b}{2}\;\;,\;\;CD=\sqrt{OF^2+OC^2}=\sqrt{\dfrac{a^2+b^2}{2}} \]

由 \(CD\geqslant OD\) 得

\[\sqrt{\dfrac{a^2+b^2}{2}}\geqslant\dfrac{a+b}{2} \]

当且仅当 \(a=b\) 时，等号成立，得证。

2、\(\dfrac{a+b}{2}\geqslant\sqrt{ab}\)

如图，点 \(E\) 在半圆 \(O\) 上，点 \(C\) 在直径 \(AB\) 上，且 \(EC\perp AB\) ，设 \(AC=a,BC=b\) .

证明：因为 \(AC=a,BC=b\)，且 \(\triangle ACE\backsim \triangle ECB\) 则

\[OE=\dfrac{a+b}{2}\;\;,\;\;CE=\sqrt{AC\cdot BC}=\sqrt{ab} \]

由 \(OE\geqslant CE\) 得

\[\dfrac{a+b}{2}\geqslant\sqrt{ab} \]

当且仅当 \(a=b\) 时，等号成立，得证。

3、\(\sqrt{ab}\geqslant\dfrac{2}{\dfrac1a+\dfrac1b}\)

如图，点 \(E\) 在半圆 \(O\) 上，点 \(C\) 在直径 \(AB\) 上，且 \(EC\perp AB\) ，\(CF\perp OE\) 设 \(AC=a,BC=b\) .

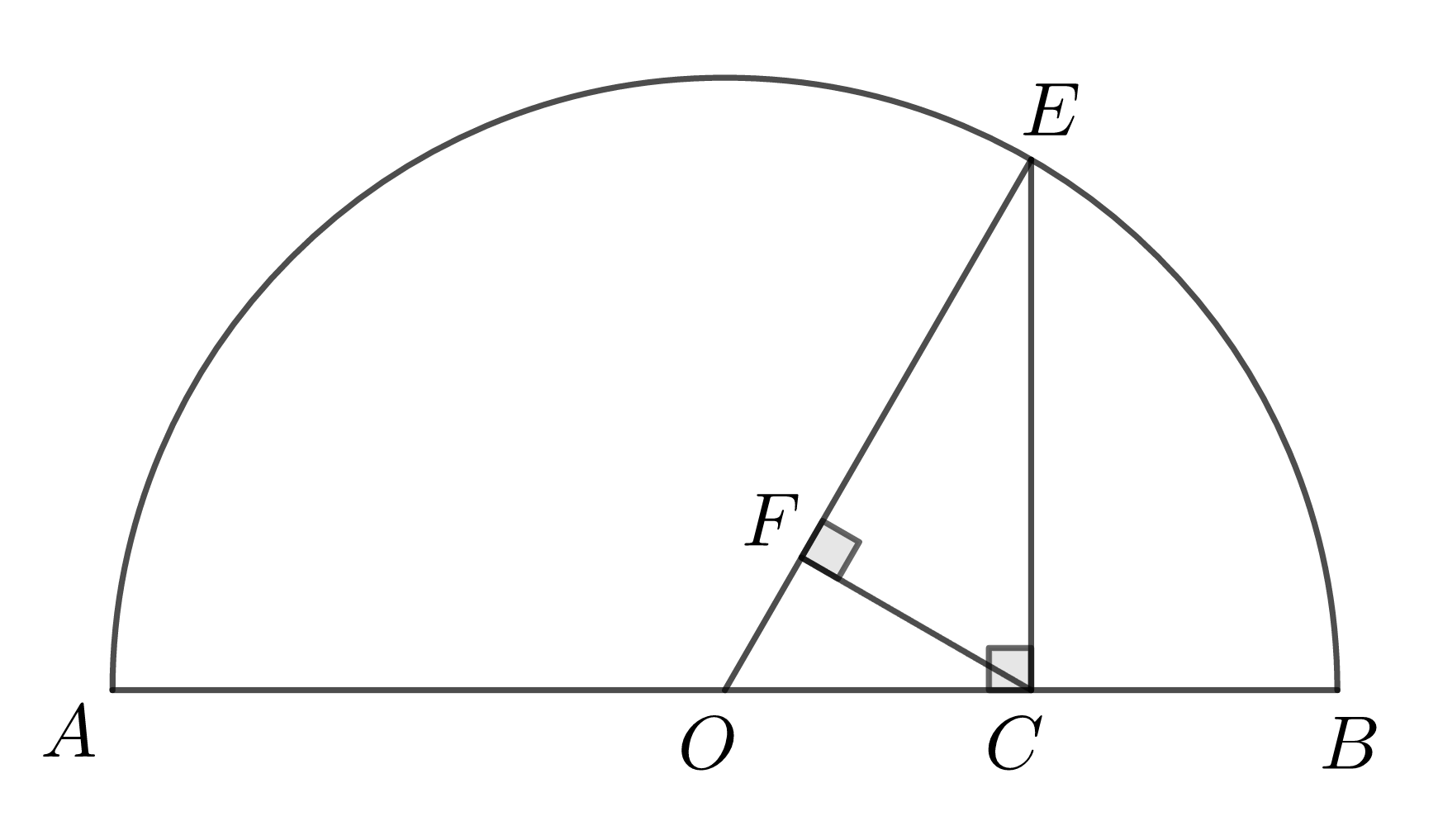
证明：由 \(\triangle OCE\backsim \triangle CFE\) 得 \(\dfrac{CE}{OE}=\dfrac{EF}{CE}\) ，则

\[EF=\dfrac{CE^2}{OE}=\dfrac{ab}{\dfrac{a+b}{2}}=\dfrac{2ab}{a+b}=\dfrac{2}{\dfrac{1}{a}+\dfrac{1}{b}} \]

由 \(CE\geqslant EF\) 得

\[\sqrt{ab}\geqslant\dfrac{2}{\dfrac1a+\dfrac1b} \]

当且仅当 \(a=b\) 时，等号成立，得证。

4、把它们画在同一个图有

由 \(CD\geqslant OD=OE\geqslant CE\geqslant EF\) 得

\[\sqrt{\dfrac{a^2+b^2}{2}}\geqslant\dfrac{a+b}{2}\geqslant\sqrt{ab}\geqslant\dfrac{2}{\dfrac1a+\dfrac1b} \]

当且仅当 \(a=b\) 时，等号成立.