设点与设线

已知椭圆 \(C；\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)\) 的右焦点为 \(F(1,0)\) ，且经过点 \(A(-2,0)\) 和点 \(B(2,0)\) .

(1) 求椭圆 \(C\) 的方程；

(2) \(M\) 和 \(N\) 是椭圆 \(C\) 上两个不同的点，四边形 \(AMBN\) 是平行四边形，直线 \(AM,AN\) 分别交 \(y\) 轴于点 \(P\) 和点 \(Q\) ，求四边形 \(APFQ\) 面积的最小值。

解析：

(1) \(\dfrac{x^2}{4}+\dfrac{y^2}{3}=1\) ；

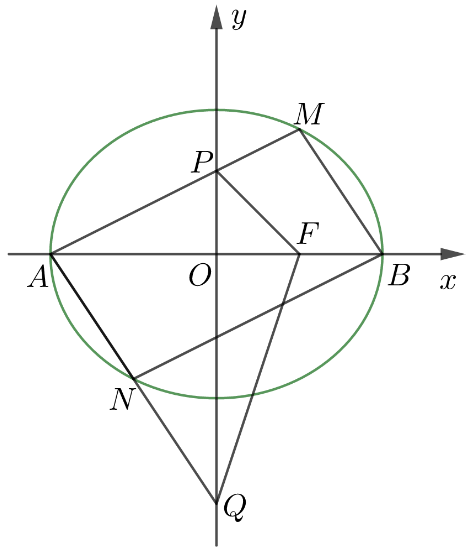
(2) 法一：设 \(M(x_0,y_0),N(-x_0,-y_0)\) ，则

\[k_{AM}\cdot k_{AN}=\dfrac{y_0}{x_0+2}\cdot\dfrac{-y_0}{-x_0+2}=\dfrac{y_0^2}{x_0^2-4} \]

因为点 \(M\) 在椭圆上，则

\[\dfrac{x_0^2}{4}+\dfrac{y_0^2}{3}=1\Longrightarrow x_0^2-4=-\dfrac{4y_0^2}{3} \]

则 \(k_{AM}\cdot k_{AN}=-\dfrac{3}{4}\)直线，设直线 \(AM\) 的斜率 \(k_{AM}=k(k>0)\) ，则 \(k_{AN}=-\dfrac{3}{4k}\) . 故有

\[\begin{cases}l_{AM}:y=k(x+2)\\l_{AN}:y=-\dfrac{3}{4k}(x+2)\end{cases}\Longrightarrow\begin{cases} P(0,2k)\\Q(0,-\dfrac{3}{2k})\end{cases} \]

则

\[S_{APFQ}=\dfrac12\cdot|AF|\cdot|PQ|=\dfrac12\cdot3\cdot(2k+\dfrac{3}{2k})\geqslant\dfrac32\cdot2\sqrt3=3\sqrt3 \]

当且仅当 \(2k=\dfrac{3}{2k}\) ，\(k=\dfrac{\sqrt3}{2}\) 时，等号成立，四边形 \(APFQ\) 面积取最小值 \(3\sqrt3\) .(由对称性得 \(k=-\dfrac{\sqrt3}{2}\) 时也成立)

法二：设 \(M(x_0,y_0),N(-x_0,-y_0)\) ，则

\[k_{AM}=\dfrac{y_0}{x_0+2}\;\;,\;\; k_{AN}=\dfrac{-y_0}{-x_0+2} \]

故得

\[\begin{cases}l_{AM}:y=\dfrac{y_0}{x_0+2}(x+2)\\[2ex]l_{AN}:y=\dfrac{y_0}{x_0-2}(x+2)\end{cases}\Longrightarrow\begin{cases} P\Big(0,\dfrac{2y_0}{x_0+2}\Big)\\[2ex]Q\Big(0,\dfrac{2y_0}{x_0-2}\Big)\end{cases} \]

则

\[S_{APFQ}=\dfrac12\cdot|AF|\cdot|PQ|=\dfrac12\cdot3\cdot\Big|\dfrac{2y_0}{x_0+2}-\dfrac{2y_0}{x_0-2}\Big|=\dfrac{3}{2}\Big|\dfrac{-8y_0}{x_0^2-4}\Big| \]

因为点 \(M\) 在椭圆上，则

\[\dfrac{x_0^2}{4}+\dfrac{y_0^2}{3}=1\Longrightarrow x_0^2-4=-\dfrac{4y_0^2}{3} \]

所以

\[S_{APFQ}=\dfrac{9}{|y_0|}\geqslant3\sqrt3 \]

当且仅当 \(y_0=\pm\sqrt3\) 时，四边形 \(APFQ\) 面积取最小值 \(3\sqrt3\) .