优化问题

一艘渔艇停泊在距海岸 \(9\) km处，今需派人送信给距渔艇 \(3\sqrt{34}\) km处的海岸渔站，如果送信人步行每小时 \(5\) km，船速每小时 \(4\) km，问应在何处登岸再步行可以使抵达渔站的时间最省？

解析

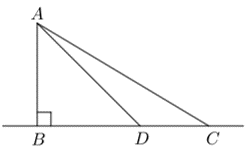
如图， A 为渔艇，C 为渔站，过 A 向海岸作垂线，垂足为 B . 若在 D 处登岸，设 \(BD=x\) ，时间为 \(t\) . 求得

\[BC=\sqrt{AC^2-AB^2}=15,AD=\sqrt{AB^2+BD^2}=\sqrt{81+x^2} \]

则

\[t(x)=\dfrac{\sqrt{81+x^2}}{4}+\dfrac{15-x}{5}，(0<x<15) \]

求得

\[t'(x)=\dfrac{x}{4\sqrt{81+x^2}}-\dfrac15 \]

令 \(t'(x)=0\)，得 \(x=12\) . 得 \(x,t'(x),t(x)\) 的变化情况如下表

\[\begin{array}{c|c|c|c}\hline x&(0,12)&12&(12,15)\\ \hline t'(x)&-&0&+\\\hline t(x)&\searrow&\dfrac{87}{20}&\nearrow\\\hline\end{array} \]

故当 \(x=12\) 时，\(t(x)\) 取最小值，用时最少，此时登岸处距渔站 \(3\) km.