Julia notebook:矩阵乘法
在本次notebook中,我们将:
- 并行化一个简单的算法
- 学习不同并行策略的performance
- 使用Julia进行实现
问题描述
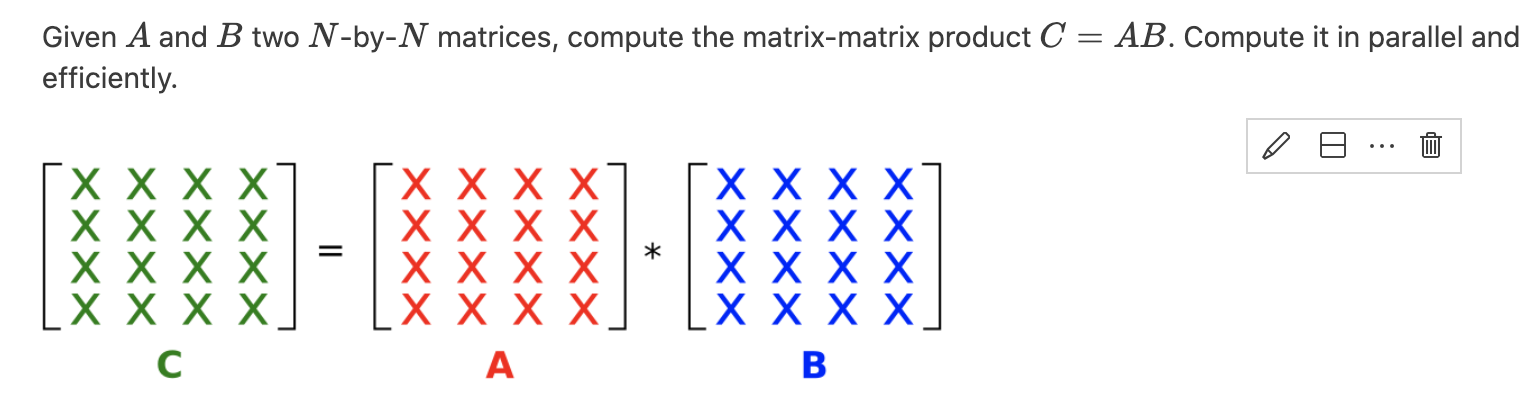
假设
- 所有矩阵,包括A,B和C都初始存储在master process
- 最终的结果会将在C中被覆盖
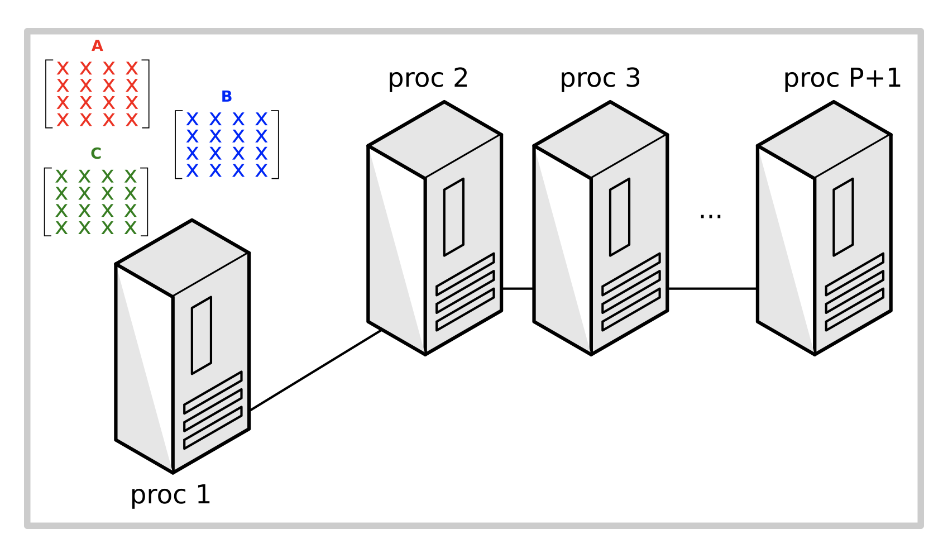
步骤
为了实现并行化,我们将遵循以下步骤:
- 确定顺序算法中可以并行化的部分
- 考虑不同的并行化策略
- 讨论这些实现的性能
串行实现
我们从最基础的串行实现开始,基于矩阵乘积的数学定义:
![]()
@everywhere function matmul_seq!(C,A,B) m = size(C,1) n = size(C,2) l = size(A,2) @assert size(A,1) == m @assert size(B,2) == n @assert size(B,1) == l z = zero(eltype(C)) for j in 1:n for i in 1:m Cij = z for k in 1:l @inbounds Cij += A[i,k]*B[k,j] end C[i,j] = Cij end end C end
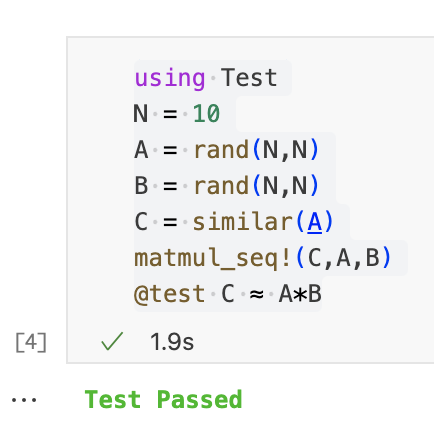
注意:如上所述,使用3个嵌套循环实现简单的矩阵乘法效率很低(内存限制)。诸如BLAS之类的库实现了更有效的实现,这些实现是在实践中使用的(例如,通过Julia中的“*”运算符)。我们认为,我们的手写实现是表达我们感兴趣的算法的简单方式。
运行下边的代码来比较我们手写函数和内置mul!函数的性能,可以看到内置函数性能要好很多。
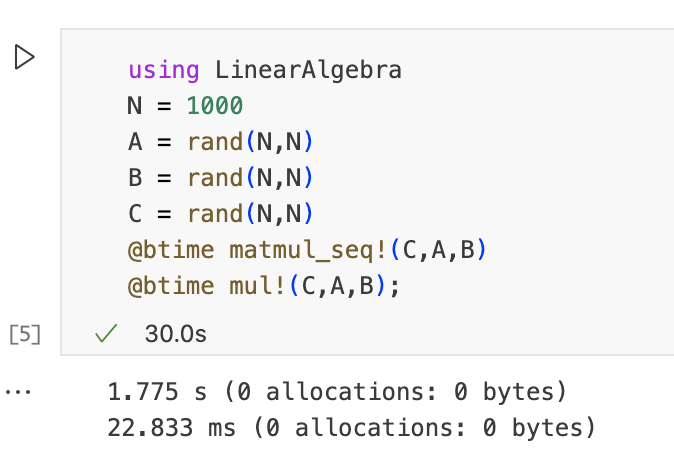

答案显而易见是O(N^3),因为有三层循环进行遍历,两层用来遍历C,填充C元素,最内层用来计算。
我们怎样可以实现并行化?
观察嵌套循环,可以发现:
- i和j的循环是可以并行化的
- k循环也可以并行化,但是需要reduction
并行算法
矩阵C的所有条目都可以进行并行计算,但是它是在分布式系统中并行解决所有这些条目的最有效解决方案吗?为了找到答案,我们将考虑不同的并行策略:
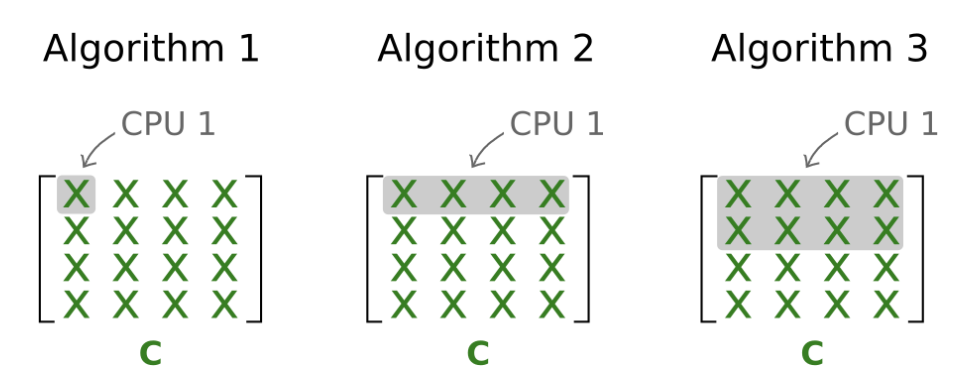
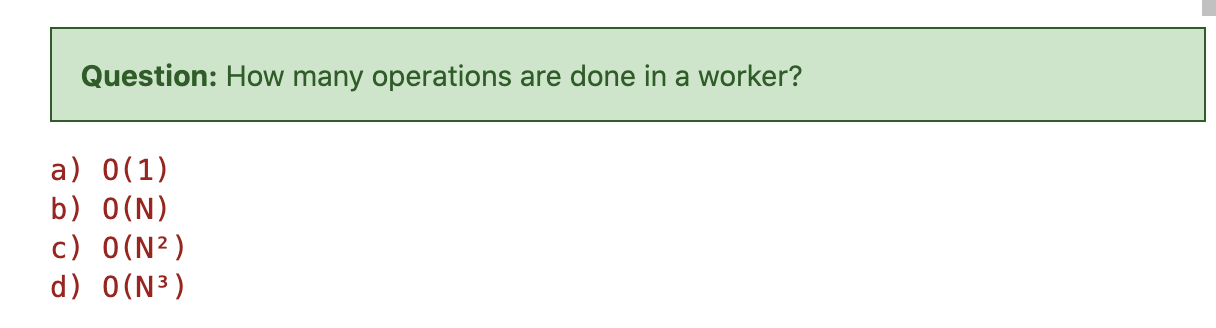
- 算法1:每个worker计算C的单个条目
- 算法2:每个worker计算单行C
- 算法3:每个worker计算C的N/P行
并行算法1
数据依赖
通过网络移动数据的成本很高,而减少数据移动是分布式计算的关键点之一。因此,我们确定worker执行计算需要的最少数据。
在算法1中,每个worker仅计算结果矩阵C的一个条目。
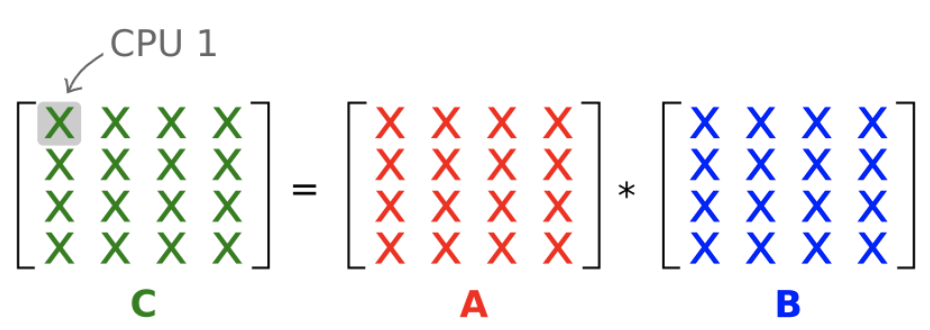

答案很显然是B,我们需要A的一行和B的一列。
实现
考虑到data dependencies,从worker的角度来看,可以按照以下步骤有效实现并行算法1:
- Worker从master接收对应的行A[i, :]和B[:, j]。
- Worker计算行和列的点积
- Worker将C[i, j]的结果发送会Master进程

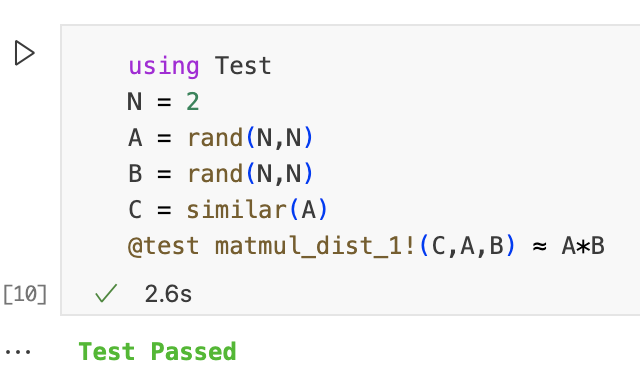
该算法在Julia中的实现可能如下:
function matmul_dist_1!(C, A, B) m = size(C,1) n = size(C,2) l = size(A,2) @assert size(A,1) == m @assert size(B,2) == n @assert size(B,1) == l z = zero(eltype(C)) @assert nworkers() == m*n iw = 0 @sync for j in 1:n for i in 1:m Ai = A[i,:] Bj = B[:,j] iw += 1 w = workers()[iw] ftr = @spawnat w begin Cij = z for k in 1:l @inbounds Cij += Ai[k]*Bj[k] end Cij end @async C[i,j] = fetch(ftr) end end C end
Performance
现在我们需要研究一下算法的性能,为此,我们将分析算法1是否能够达到最优的加速比。P个加速器上的并行加速比定义为:

Experimental speedup
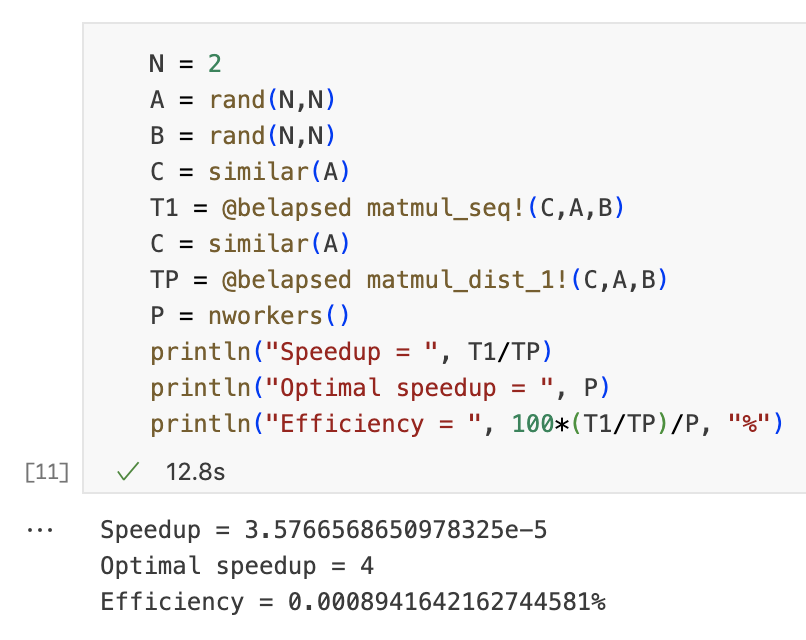
接下来我们测量一下算法1的加速比,我们达到最优了吗?
N = 2 A = rand(N,N) B = rand(N,N) C = similar(A) T1 = @belapsed matmul_seq!(C,A,B) C = similar(A) TP = @belapsed matmul_dist_1!(C,A,B) P = nworkers() println("Speedup = ", T1/TP) println("Optimal speedup = ", P) println("Efficiency = ", 100*(T1/TP)/P, "%")
Communication overhead
由于通信通常是分布式算法中的主要瓶颈,因此我们希望减少工作线程中每单位计算的通信量。让我们计算算法1的通信开销,这将帮助我们理解为什么该算法的加速比如此糟糕。

答案是b,很显然。
答案是b,只有一个循环,计算乘积。
因此我们可以得出结论:

换句话说,通信成本和计算成本处于同一数量级。由于实际系统中通信速度要慢几个数量级,因此worker之间的运行时间主要由通信决定。这解释了为什么我们的加速比如此糟糕。
并行算法2
让我们研究下一个算法,看看是否可以通过增加每个并行任务的粒度(即工作量)来提高效率。在并行算法2中,每个worker计算C的整行。
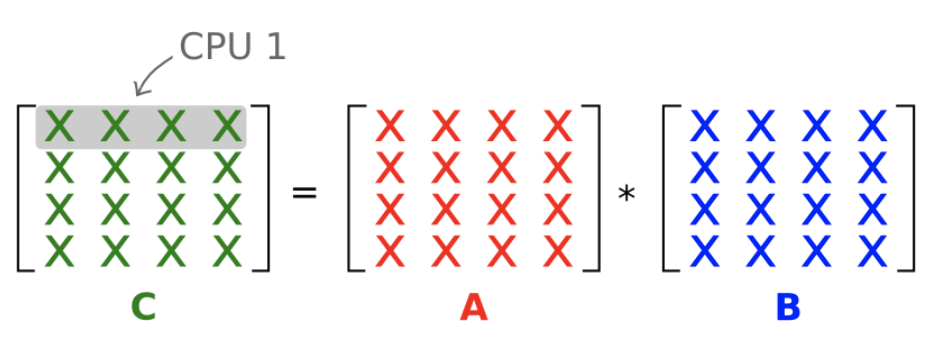
Data dependencies

答案是d,因为计算C的一行需要用A的一行依次乘以B的每一列。
Implementation
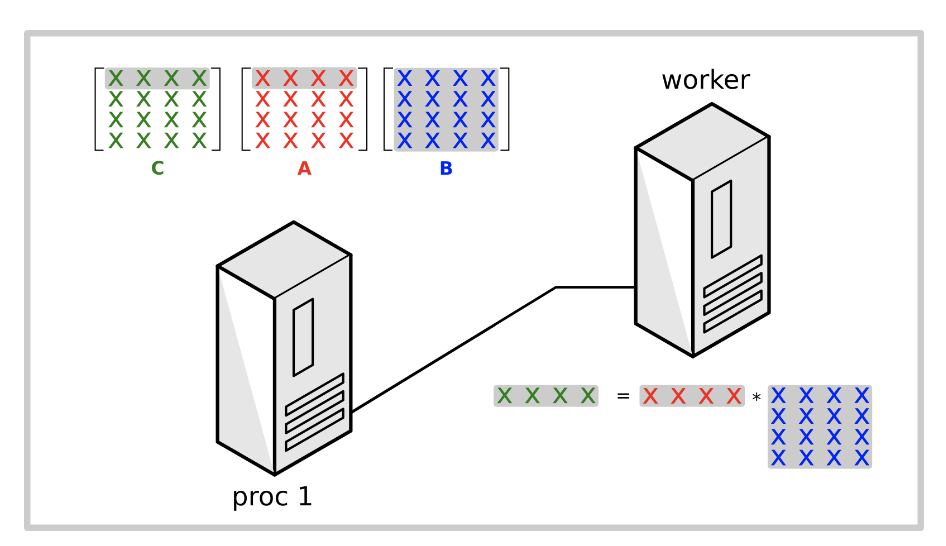
主要实现步骤如下:
- worker从master进程接收相应的矩阵A的行A[i, :]和矩阵B
- worker计算A的行和矩阵B的乘积
- worker将计算的结果(矩阵C的行C[i, :])发送回master进程
Julia代码实现如下:
function matmul_dist_2!(C, A, B) m = size(C,1) n = size(C,2) l = size(A,2) @assert size(A,1) == m @assert size(B,2) == n @assert size(B,1) == l z = zero(eltype(C)) @assert nworkers() == m iw = 0 @sync for i in 1:m Ai = A[i,:] iw += 1 w = workers()[iw] ftr = @spawnat w begin Ci = fill(z,n) for j in 1:n for k in 1:l @inbounds Ci[j] += Ai[k]*B[k,j] end end Ci end @async C[i,:] = fetch(ftr) end C end
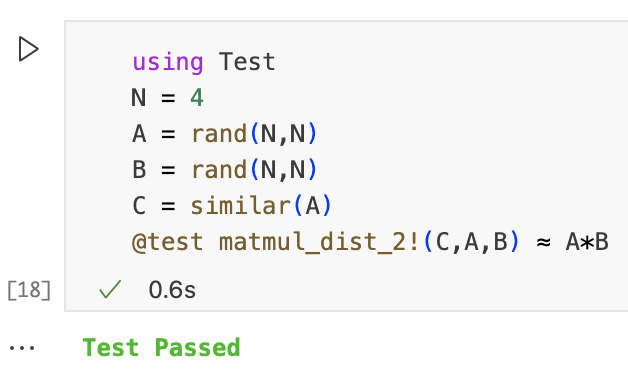
Experimental speedup
N = 4 A = rand(N,N) B = rand(N,N) C = similar(A) T1 = @belapsed matmul_seq!(C,A,B) C = similar(A) TP = @belapsed matmul_dist_2!(C,A,B) P = nworkers() println("Speedup = ", T1/TP) println("Optimal speedup = ", P) println("Efficiency = ", 100*(T1/TP)/P, "%")

Complexity
加速比仍然远没有达到最佳,让我们研究一下该算法的通信开销。请记住,算法2包含以下的步骤:
- worker从master进程接收对应的行A[i, :]和矩阵B
- worker计算A[i, :]乘以B的乘积
- 工作进程将行C[i, :]的结果发送回主进程

答案是b,此时通信需要传输整个矩阵B,因此是O(N^2),计算也是两层循环,复杂度也为O(N^2)。
可以看到,即使我们增加了粒度,通信和计算仍然是相同数量级。
并行算法3
让我们通过在worker中计算多行C来进一步增加并行任务的粒度,每个worker计算C的N/P连续行,P是worker的数量。
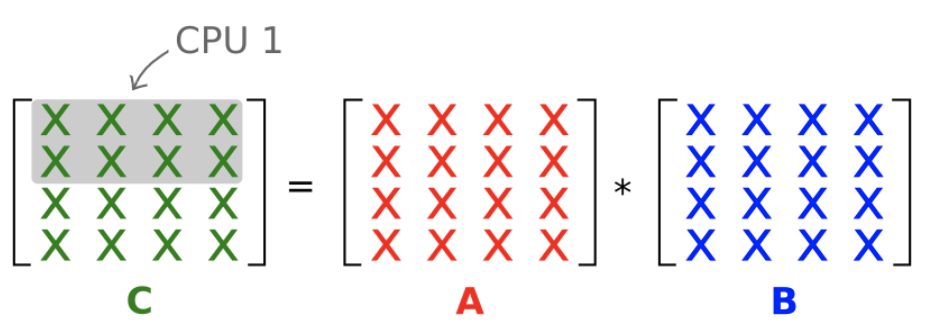
Data dependencies

答案是c,我们只需要A的对应几行和整个矩阵B。
Implementation
算法3的主要步骤如下:
- worker从master进程接收对应的行A[rows, :]和矩阵B
- worker计算A[rows, :]乘以B的乘积
- worker将C[rows, :]的结果发送回master
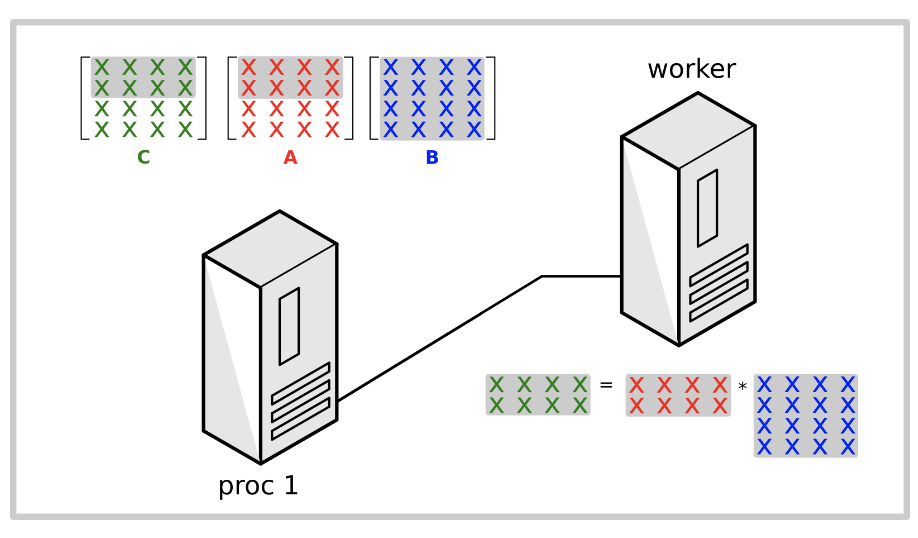
Communication overhead

答案是b,通信计算的overhead仍为O(N^2),那么计算的overhead有什么变化呢?
首先要有一个N/P的循环,接着要有一个N的循环,然后计算每一个元素,需要有一个N的循环。因此是O(N^3/P)。
在这种情况下,通信和计算之间的比率是O(P/N)。如果矩阵大小N远大于worker数量P,则通信开销O(P/N)可以忽略不计,这使可扩展的实现成为可能。
Summary
下表是对三种算法的一个总结:
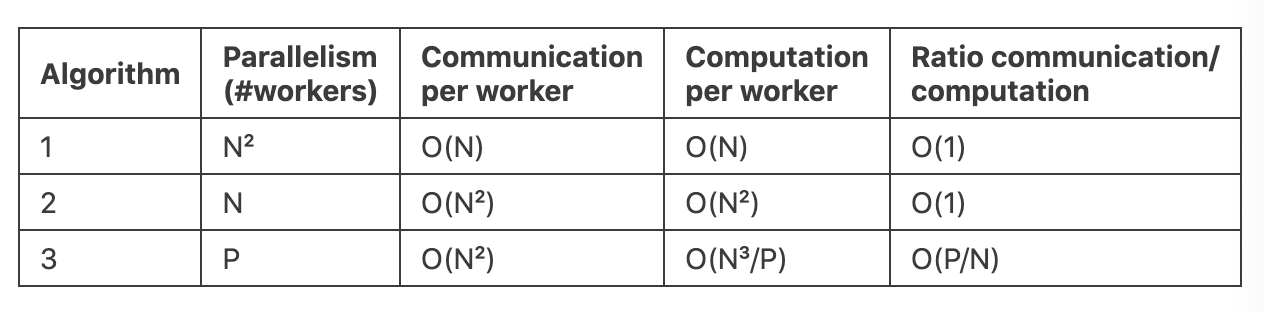
- 矩阵乘法是可以并行计算的,至少在理论上,结果矩阵中的所有条目都可以并行计算
- 然而,由于通信开销,我们无法利用分布式系统中所有潜在的并行性
- 我们需要足够大的粒度才能接近最佳的加速比
Exercise
练习1
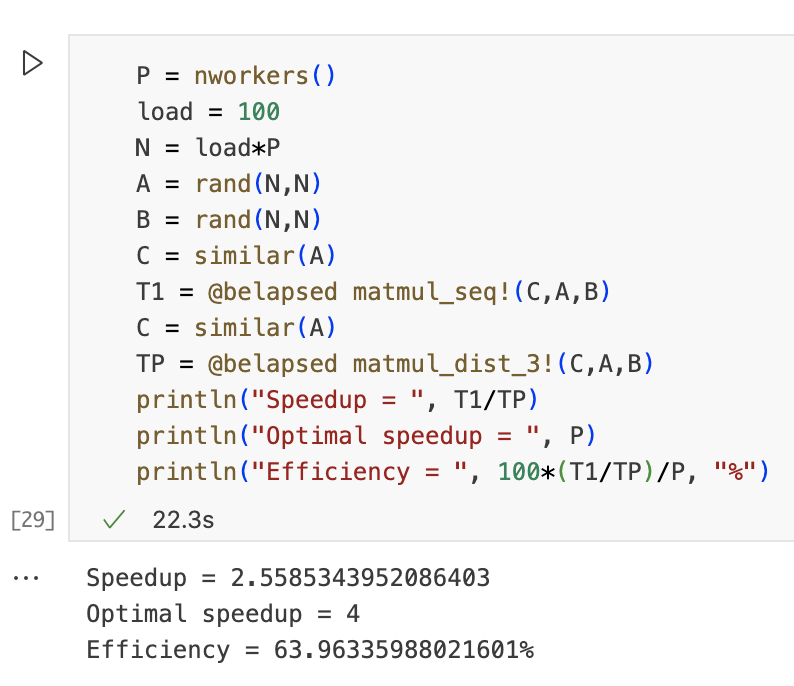
实现一下上边的算法3,为了简单起见,假设C的行数是工人数量的倍数。
function matmul_dist_3!(C,A,B) m = size(C,1) n = size(C,2) l = size(A,2) @assert size(A,1) == m @assert size(B,2) == n @assert size(B,1) == l @assert mod(m,nworkers()) == 0 nrows_w = div(m,nworkers()) @sync for (iw,w) in enumerate(workers()) lb = 1 + (iw-1)*nrows_w ub = iw*nrows_w A_w = A[lb:ub,:] ftr = @spawnat w begin C_w = similar(A_w) matmul_seq!(C_w,A_w,B) C_w end @async C[lb:ub,:] = fetch(ftr) end C end @everywhere function matmul_seq!(C,A,B) m = size(C,1) n = size(C,2) l = size(A,2) @assert size(A,1) == m @assert size(B,2) == n @assert size(B,1) == l z = zero(eltype(C)) for j in 1:n for i in 1:m Cij = z for k in 1:l @inbounds Cij = Cij + A[i,k]*B[k,j] end C[i,j] = Cij end end C end
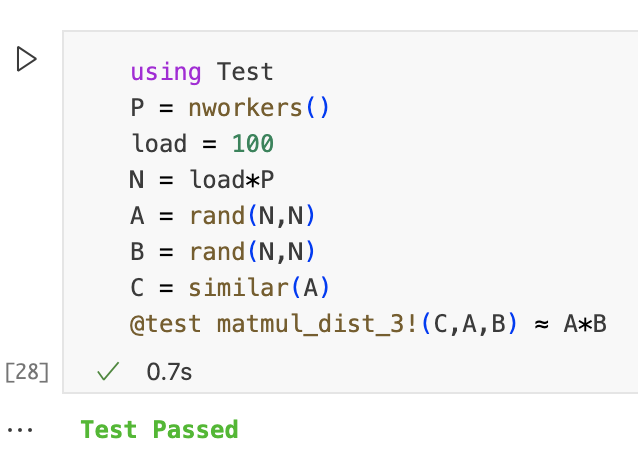
测试通过,接下来我们看一下加速比等性能。
练习2
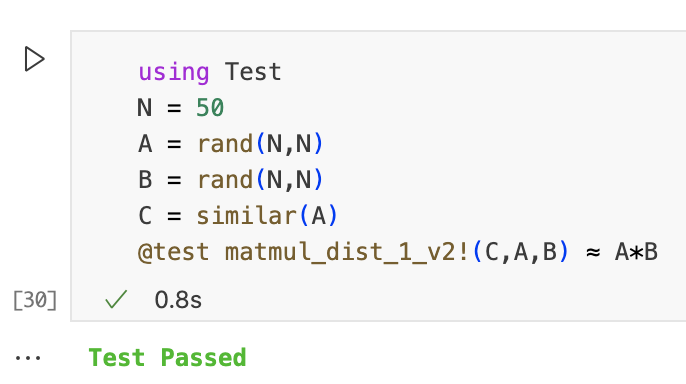
算法1的实现非常不切实际,我们需要与结果矩阵C中的条目一样多的处理器。对于1000*1000的矩阵,我们需要一台具有100万个进程的超级计算机。我们可以通过使用更少的处理器并在任何可用进程中生成条目的计算来轻松解决此问题。
function matmul_dist_1_v2!(C, A, B) m = size(C,1) n = size(C,2) l = size(A,2) @assert size(A,1) == m @assert size(B,2) == n @assert size(B,1) == l z = zero(eltype(C)) @sync for j in 1:n for i in 1:m Ai = A[i,:] Bj = B[:,j] ftr = @spawnat :any begin Cij = z for k in 1:l @inbounds Cij += Ai[k]*Bj[k] end Cij end @async C[i,j] = fetch(ftr) end end C end
通过这个新的实现,我们计算任意大小的矩阵乘法,并且worker的数量固定。
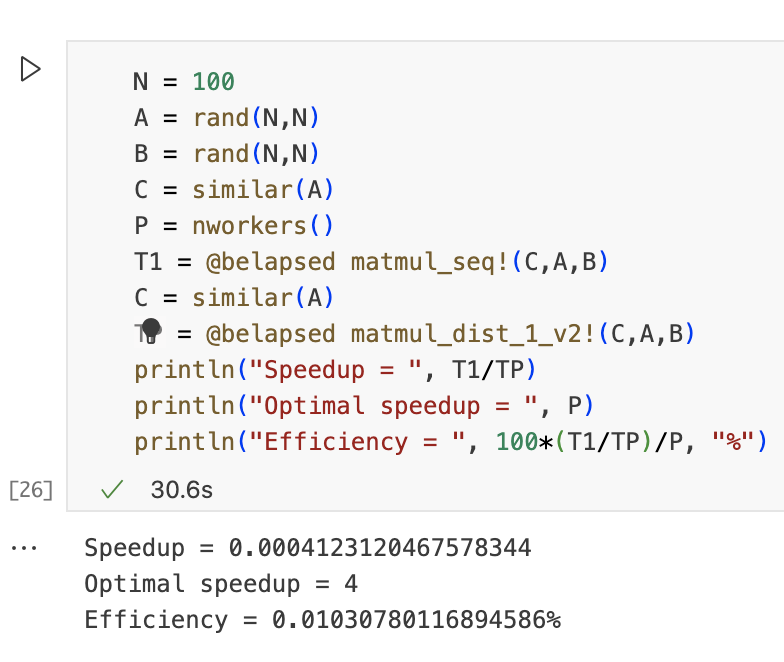
运行下边的代码测试实现的性能。请注意,我们距离最佳的加速比还很远。为什么呢?为了回答这个问题,我们计算该实现的communication和computation比率,并对所获得的结果进行推理。在此实现中,worker生成的次数平均为N^2/P。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号