2. Haskell简单实践

我们要做的第一件事就是运行ghc的交互模式并调用一些函数来获得对haskell的基本感觉，打开终端输入ghci，我们会得到如下的反应：

 做一些简单的算术：

 我们也可以在一行上使用多个运算符，并遵守所有常见的优先级规则，我们可以使用括号来明确优先级或更改优先级。

 需要注意的是，如果我们想要一个负数，最好用括号将其扩起来，例如需要执行 5 * (-3)。

布尔代数也非常简单，&&表示布尔值和，||表示布尔值或，not表示否定True或者False。

 equality是这样完成的，其中/=是不等于的意思：

 那么5 + "llama"或者"5 == True"怎么样呢，如果我们尝试第一个片段，会收到错误消息：

报错信息告诉我们，llama不是一个数字，+仅适用于被视为数字的事物，==适用于任何可以比较的事物，必须是同一类型的东西。

我们一直在使用函数，*是一个接受两个数字并将它们相乘的函数，我们通过将其夹在中间来称呼它，这就是我们说的中缀函数。大多数不与数字一起使用的是前缀函数。

函数通常是前缀的，从现在开始我们不会明确声明函数是前缀形式，我们只是假设。在大多数命令式语言中，通过编写函数名称，然后将参数写在括号中（通常用逗号隔开）来调用函数。在Haskell中。通过编写函数名称、空格和参数来调用函数，参数之间用空格分隔。首先，我们将尝试调用Haskell中最无聊的函数之一。

succ函数接受具有已定义后继者的任何内容并返回该后继者。我们只是用空格分隔函数名称和参数。调用具有多个参数的函数也很简单。函数max和min接受两个可以排序的东西（比如数字）：

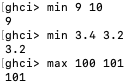
函数应用，通过在函数后边添加空格然后键入参数来调用函数，具有最高的优先级，这对我们来说意味着两个陈述是等价的：

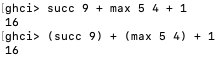
然而，如果我们想得到数字9和10乘积的后继，不能写succ 9 * 10，因为这会得到9的后继，然后乘以10，我们必须写succ (9 * 10)。

如果一个函数有两个参数，我们也可以通过反引号将其括起来成为中缀函数。例如，div函数接受两个整数并在它们之间进行整数除法。div 92 10 的结果是9。但是当我们这样称呼它时，可能会混淆是哪个数字在做除法以及哪个数字被除法。我们可以通过执行92 'div' 10将其称为中缀函数，这样就清晰很多。

许多命令式语言倾向于这样的观念：括号应该表示函数应用。例如，在C中，可以使用括号来调用foo()、bar(1)等函数。在Haskell中，空格用于函数应用，所以应该写成foo、bar 1。因此，如果看到类似bar (bar 3)的内容，并不意味着bar是以bar和3位参数调用的。这意味着我们首先用3调用函数bar作为参数来获取一些数字，然后我们用数字再次调用bar。

+适用于证书和浮点数，实际上是任何可以被视为数字的数字，创建一个test.hs文件，

然后使用:l test来加载脚本，就可以使用我们定义的函数了。

 增加一个函数doubleUs x y = x*2 + y*2，然后进行测试：

 我们也可以从创建的其他函数中调用自己的函数，我们可以这样重新定义doubleUs：doubleUs x y = doubleMe x + doubleMe y。Haskell中的函数不必按照特定顺序，因此我们无论先定义doubleMe再定义doubleUs都没有关系。

现在我们创建一个将数字乘以2的函数，前提是该数字小于或等于100。

 这里介绍了Haskell的if语句，else是强制的。在命令式语言中，如果不满足条件，可以跳过几个步骤，但是在Haskell中，每个表达式和函数必须返回一些内容。我们可以将if写在一行中，但是可读性较差。if后边跟一个表达式，表达式基本上是一段返回值的代码。5是一个表达式，因为返回5，4+8是一个表达式，因为返回x和y的总和。因为else是强制性的，所以if总会返回一些内容，这就是它是表达式的原因。如果我们想为上一个函数中生成的每个数字加1，可以这样编写主函数：

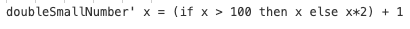
 如果我们省略括号，则仅当x不大于100时才会+1，注意函数名称末尾的‘，没有任何特殊含义，是在函数名称中使用的有效字符。我们通常用’来表示函数的严格版本（非惰性函数）或函数或变量的稍微修改版本。因为‘是函数中的有效字符，所以我们可以创建这样的函数。

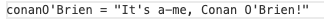
 有两件事值得注意，在函数中，我们没有将Conan的名字大写，这是因为函数不能以大写字母开头。第二件事是这个函数不带任何参数，当函数不带参数时，我们通常说它是一个definition或者name。因为一旦定义了name和function，我们就无法改变它们的含义。conanO'Brien和字符串"It's a-me, Conan O'Brien!"可以互换使用。

 

列表

Haskell中的列表十分有用是最常用的数据结构，我们将介绍列表、字符串列表和列表推导式的基础知识。

在Haskell中，列表是同质数据结构，存储多个相同类型的元素。

注：我们可以使用let关键字在GHCI中定义名称，执行let a = 1相当于在脚本中写入a = 1然后加载。

 因为字符串是列表，所以我们可以对它们使用列表函数，这非常方便。一个常见的任务是将两个列表放在一起，通过++运算符实现。

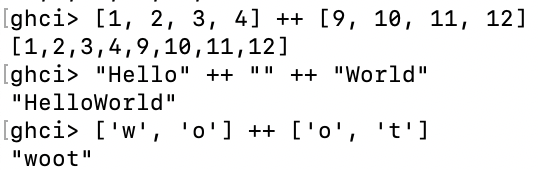
在长字符串上重复使用++时要小心 ，当将两个列表放在一起时，即将一个单例列表附加到一个列表中，例如[1,2,3] ++ [4]，Haskell必须遍历左侧的整个列表++。当处理不太大的列表时，不是问题，但是将某些内容放在包含5000万个条目的列表末尾需要一段时间。使用：运算符，也称为cons运算符，将某些内容放在列表的开头是即时的。

 [1, 2, 3]实际上是1:2:3:[]的语法糖，[]是一个空列表，如果我们在它前面加上3，就变成[3]，如果加上2，就变成[2, 3]。

注意：[], [[]], [[],[],[]]都是不同的东西，第一个是一个空列表，第二个是包含一个空列表的列表，第三个是包含三个空列表的列表。

如果想通过索引从列表中获取元素，使用!!，索引从0开始。

 列表可以进行嵌套：

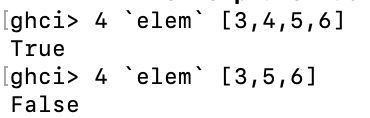
 列表中的列表可以具有不同的长度，但是不能有不同的类型。如果列表的内容可以进行比较，那么列表就可以进行比较，使用<，<=，>=比较列表时，按照字典顺序进行比较，首先比较头部，如果相等，就比较第二个元素，以此类推。

 还有一些对列表进行操作的基本函数，不要在空列表上使用这些函数：

 

 

 

Texas Ranges

范围是一种创建列表的方法，列表是可枚举元素的算术序列。要创建包含从1到20的所有自然数的列表，只需编写[1..20]。

 我们还可以指定一个步骤，如果想要1-29之间所有的偶数，或者每三个数：

只需用逗号分隔前两个元素，然后指定上限。虽然非常聪明，但带有步骤的范围并不像某些人期望的那么聪明。您无法执行[1,2,4,8,16..100]并期望获得 2 的所有幂。首先，因为您只能指定一个步骤。其次，因为一些非算术序列如果仅由其中的几个第一项给出，那么是不明确的。

要得到从20到1的所有数字的列表，不能只执行[20..1]，必须执行[20,19..1]。

在范围内使用浮点数要小心，因为它们并不完全精确，它们在范围内的使用可能会产生一些非常奇怪的结果。

建议不要再列表范围中使用它们。

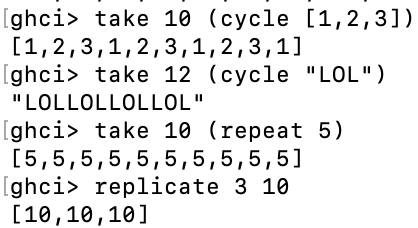
可以使用范围来创建无限列表，只需不指定上限即可。现在，我们来看看如何获得13的前24个倍数。

Haskell很懒，他不会立即尝试计算无限列表，因为它永远不会完成。它会等着看你想从无限列表中获得什么，显然在这里是前24个元素。如下是一些产生无限列表的函数：

 

List comprehension

列表推导式与集合推导式子十分相似，目前我们将坚持获取前10个偶数，可以使用的列表理解是[x*2 | x <- [1..10]]。x是从[1..10]中提取的，对于[1..10]中的每个元素，我们已经绑定到x，得到该元素然后加倍。

如上所示，可以向推导式添加一个条件（或谓词）。谓词位于绑定部分之后，并用逗号将其分隔开。假设我们只需要翻倍后大于等于12的元素。

我们获得一个数字列表，并通过谓词过滤了它们。现在再举一个例子，假设我们想要一个将每个大于10的奇数换成"BANG"的推导式，每个小于10的奇数都会发出"BOOM"的声音。如果不是奇数就从列表中删除。

我们可以包含几个谓词，如果想要10到20之间除13、15或19之外的所有数字，我们会这样做：

我们不仅可以在列表推导式中拥有多个谓词（一个元素必须满足包含在结果列表中的所有谓词），我们还可以从多个列表中进行绘制，推导式会给出制定列表的所有组合，然后通过我们提供的函数连接起来。如果我们不过滤，则从两个长度为4的列表中提取的推导式生成的列表的长度将为16。

 如果是形容词和名词呢：

现在我们定义我们自己length函数：let length' xs = sum [1 | _ <- xs]。

_意味着我们不关心将从列表中提取什么，将所有元素替换为1，然后将其相加，得到列表的长度。

因为字符串是列表，因此我们可以用列表推导式来处理和生成字符串，这是一个函数，接受一个字符串并从中删除大写字母之外的所有内容。

如果您对包含列表的列表进行操作，则也可以使用嵌套列表推导式。一个列表包含多个数字列表。让我们删除所有奇数而不展平列表。

 

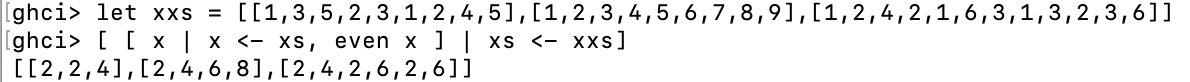
Tuples

在某些方面，元组就像列表，是将多个值存储到单个值中的一种方式。数字列表就是数字列表，这是它的类型，无论只有一个数字还是无数个数字都没有关系。然而，当确切地想知道要组合多少个值并且类型取决于有多少个组件以及组件的类型时。就会使用元组，用括号表示，用逗号分隔。

另一个关键区别是，它们不需要同质，可以包含多种类型的组合。

如何在Haskell中表示二维向量，一种方法是使用列表，如果想将几个向量放入一个列表中来表示二维平面上的形状点怎么办，可以用类似[[1,2], [8,11],[4,5]]。大小为2的元组也称为对，是它自己的类型。您也无法创建像[(1,2),("One",2)]这样的列表，因为列表的第一个元素是一对数字，第二个元素是由字符串和数字组成的对。元组还可以用来表示各种各样的数据。例如，如果我们想在 Haskell 中表示某人的姓名和年龄，我们可以使用三元组：("Christopher", "Walken", 55)。

当您预先知道某些数据应该有多少个组件时，请使用元组。元组更加严格，因为每个不同大小的元组都是其自己的类型，因此您不能编写通用函数来将元素附加到元组 - 您必须编写一个函数来附加到一对，一个函数用于附加到三元组、附加到 4 元组的一个函数等。

虽然存在单例列表，但不存在单例元组这样的东西。当你仔细考虑时，这并没有多大意义。单例元组只是它包含的值，因此对我们没有任何好处。

与列表一样，如果可以比较元组的组成部分，则可以将元组相互比较。只是您不能比较两个不同大小的元组，而您可以比较两个不同大小的列表。

fst接受一对并返回其第一个分量，snd接受一对并返回其第二个分量。

这些函数只能成对运行，不适用于三元组、四元组、五元组等。zip函数它需要两个列表，然后通过将匹配的元素连接成对，将它们压缩到一个列表中。这是一个非常简单的功能，但它有很多用途。当您想要以某种方式组合两个列表或同时遍历两个列表时，它特别有用。

它将元素配对并生成一个新列表。第一个元素与第一个元素匹配，第二个元素与第二个元素匹配，等等。请注意，因为对中可以有不同的类型，所以zip可以采用两个包含不同类型的列表并将它们压缩。如果列表的长度不匹配会发生什么？

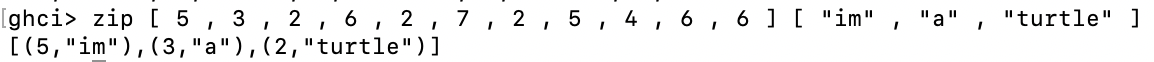
 较长的列表只是被截断以匹配较短的列表的长度。因为 Haskell 很懒，所以我们可以用无限列表压缩有限列表：

这是一个结合了元组和列表推导式的问题，哪个直角三角形的所有边都是整数且所有边都等于或小于 10，其周长为 24？首先，我们尝试生成边长等于或小于 10 的所有三角形：

我们只是从三个列表中进行绘制，我们的输出函数将它们组合成一个三元组。如果您通过在 GHCI 中输入三角形来评估这一点，您将获得边长小于或等于 10 的所有可能三角形的列表。接下来，我们将添加一个条件，即它们都必须是直角三角形。我们还将修改此函数，考虑到 b 边不大于斜边且 a 边不大于 b 边。现在，我们只需修改函数，表示我们想要周长为 24 的函数。