深度学习入门（6）

参考原文链接🔗：https://developer.aliyun.com/article/96427

上节我们提到，感知机无法解决“异或”的问题，解决这个问题的关键在于，是否能解决非线性可分问题。要解决这个问题，简单来说，就是使用更复杂的网络，也就是多层前馈网络。

多层网络搞定“异或”问题

深度学习是一个包括很多隐含层的复杂网络结构，感知机无法解决“非线性可分”问题，是因为它过于简单。

要想解决“异或”问题，就要让网络复杂起来。这是因为，复杂的网络，表征能力比较强。按照这个思路，我们在输入层和输出层之间，增加一层神经元，称为隐含层（又称“隐层”）。这样一来，隐含层和输出层中的神经元都拥有激活函数。假设各个神经元的阈值均为0.5，这样就实现了“异或”功能。 

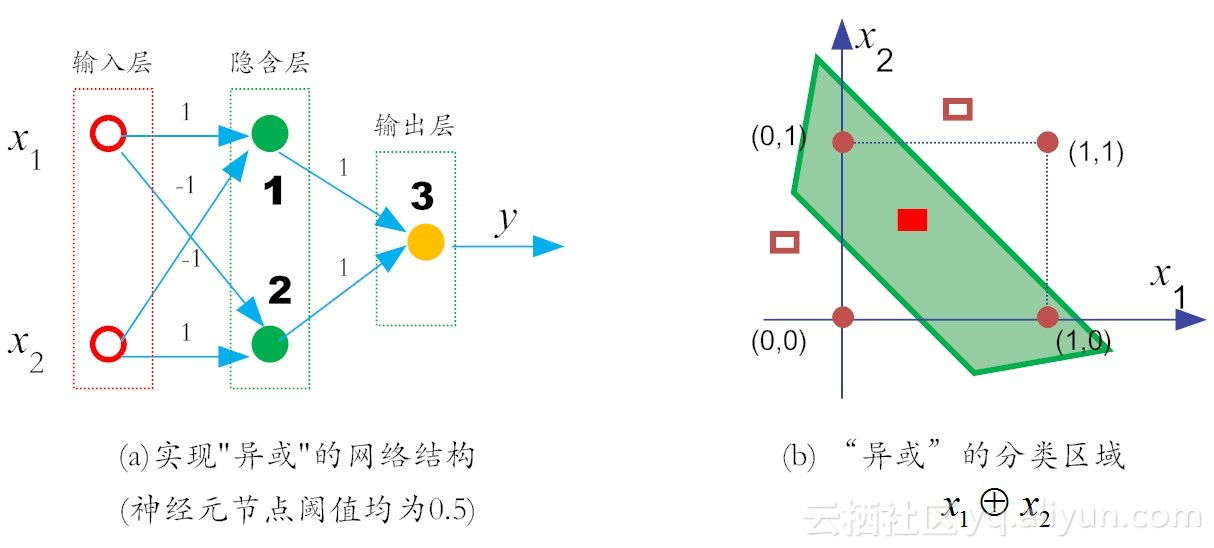
假设在a图中所示的神经元（即实心圆）的激活函数依然是阶跃函数（即sgn函数），那么它的输出规则十分简单：当x>0时，f(x)输出为1，否则输出0。

那么对于x1和x2相同（均为1）时，对于在隐含层的神经元1有：

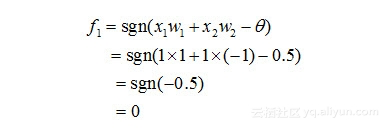
 类似地，对于在隐含层的神经元2有：

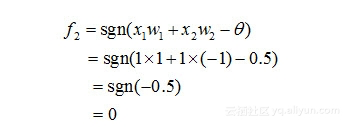
然后，对于输出层的神经元3而言，这时f1和f2是它的输入，于是有：

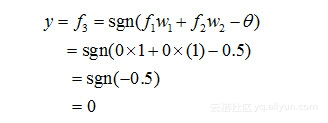
 也就是说，二者同为1时，输出为0。

对于x1和x2不同时，对于在隐含层的神经元1有：

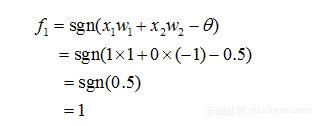
 类似地，对于在隐含层的神经元2有：

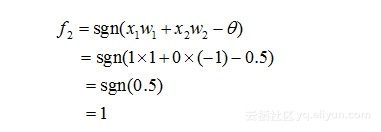
对于神经元3，有：

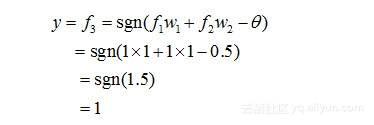
不失一般性，x1和x2的角色地位是可以互换的，因此，上面的两层感知机，可以实现“异或”功能。在这里，网络中的权值和阈值是我们实现给定的，而实际上，它们是由神经网络自己通过反复“试错”学习而来的。

简单来说，深度学习，就是包括很多隐含层的神经网络学习，这里的“深”即意味着“层深”。

多层前馈神经网络

更一般的，常见的多层神经网络如图所示，在这种结构中，每一层神经元仅仅与下一层的神经元完全链接，在同一层，神经元彼此之间不连接，而且跨层的神经元，彼此间也不相连。这种被简化的神经网络结构，称为“多层前馈神经网络”。

 

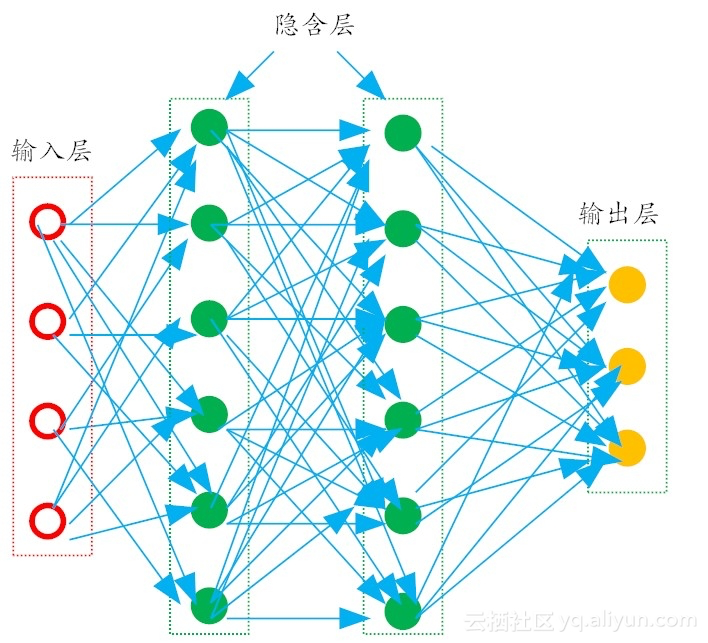
在多层前馈神经网络中，输出层神经主要用于接收外加的输入信息，在隐含层和输出层中，都有内置的激活函数，可以对输入信号进行加工处理，最终的结果，由输出层“呈现”出来。

 这里需要说明的是，神经元中的激活函数，并不限于我们之前提到的阶跃函数、Sigmod函数，还可以是现在深度学习常用的ReLU和sofmax等。

简单来说，神经网络的学习过程，就是通过根据训练数据，来调整神经元之间的连接权值以及每个功能神经元的输出阈值。换言之，神经网络需要学习的东西，就蕴含在连接权值和阈值中。

拟人化来说，对于识别某个对象来说，神经网络中的连接权值和阈值，就像是它关于这个对象的“记忆”，大脑对于事物和概念的记忆，不是存储在某个单一的地点，而是像分布式地存在于一个巨大的神经元网络之中。

分布式表征，是人工神经网络研究的一个核心思想，简单来说，就是当我们表达一个概念时，神经元与概念之间不是一对一对应映射存储的，他们的关系是多对多。具体而言，就是一个概念可以用多个神经元共同定义表达，同时一个神经元也可以参与多个不同概念的表达，只不过占的权重不同。

举例来说，对于“小红汽车”这个概念，如果用分布式特征地表达，那么可能是一个神经元代表大小（形状：小），一个神经元代表颜色（颜色：红），还有一个神经元代表车的类别（类别：汽车）。当这三个神经元同时被激活时，就可以准确的描述我们要表达的物体。

分布式表征表示有很多优点，其中最重要的一点，是当部分神经元发生故障时，信息的表达不会出现覆灭性的破坏。

前文提到，对于相对复杂的前馈神经网络，其各个神经元之间的链接权值和其内部的阈值，是整个神经网络的灵魂所在，它需要通过反复训练，方可得到合适的值。而训练的抓手，就是实际输出值和预期输出值之间存在的“落差”（可以称之为“误差”）。

下面，我们来讲述如何用“落差”来反向调节网络参数。

我们知道，在机器学习中的“有监督学习”算法里，在假设空间F中，构造一个决策函数f，对于给定的输入X，由f(X)给出相应的输出Y，这个实际输出值Y和原先预期值Y'可能不一致。于是我们需要定义一个损失函数，也有人称之为代价函数来度量这两者之间的“落差”程度。这个损失函数通常记作L(Y,Y') = L(Y,f(X))，为了方便起见，这个函数的值为非负数（请注意：在这里我们大写Y和Y'，分别表示的是一个输出值向量和期望值向量，它们分别包括多个不同对象的实际输出值和期望值）。

常见的损失函数有如下3类：

（1）0-1损失函数：

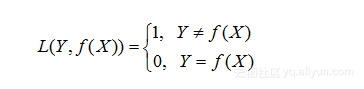
（2）绝对损失函数

 

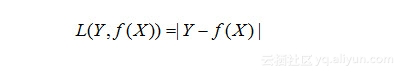
（3）平方损失函数

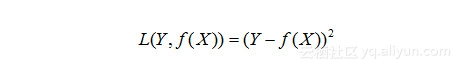
损失函数值越小，说明实际输出和预期输出的差值就越小，也就说明我们构建的模型越好。

对于第一类损失函数，简单来说，达到目标了，输出为0（没有落差），没有达到输出1（仍需努力）。

对于第二类损失函数更具体，避免正负值干扰，干脆取一个绝对值。

对于第三类函数，同样达到了避免正负值干扰，但是为了计算方便（主要是为了求导），通常还会在前面加一个“1/2”，这样求导，系数就可以变为“1”了：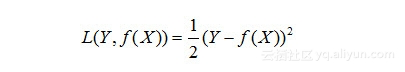

当然，为了计算方便，还可以用对数损失函数，这样做的目的，主要是便于使用最大似然估计的方法来求极值。

损失函数的作用是可以用它反向配置网络中的权值，让损失最小。神经网络学习的本质，就是利用“损失函数”，来调节网络中的权重。

总体来说，有两大类方法比较好使，第一种方法就是“误差反向传播（简称BP）”。简单来说，就是首先随机设定初值，然后计算出当前网络的输出，然后根据网络输出与预期输出之间的差值，采用迭代的算法，反方向地去改变前面各层的参数，直至网络收敛稳定。

BP反向传播算法十分好用，直接把纠错的运算量，降低到只和神经元数目本身成正比的程度。但是实际应用起来，有很多问题，比如，在一个层次较多的网络中，当它的残差反向传播到最前面的层（即输入层），其影响已经变得十分小，甚至出现梯度扩散，严重影响训练精度。

其实，这也是容易理解的。因为在“信息论”中有个信息逐层缺失的说法，就是说信息在逐层处理时，信息量是不断减少的。例如，处理A信息而得到B，那么B所带的信息量一定是小于A的。这个说法，再往深层次的探寻，那就是信息熵的概念了。推荐读者阅读一部影响我世界观的著作《熵：一种新的世界观》。

根据热力学第二定律我们知道，能量虽然可以转化，但是无法100%利用。在转化过程中，必然会有一部分能量会被浪费掉。这部分无效的能量，就是“熵”。把“熵”的概念，迁移到信息理论，它就表示“无序的程度”。

当一种形式的"有序化（即信息）"，转化为另一种形式的"有序化"，必然伴随产生某种程度上的"无序化（即熵）"[6]。依据这个理论，当神经网络层数较多时（比如说大于7层），BP反向传播算法中“误差信息”，就会慢慢“消磨殆尽”，渐渐全部变成无序的“熵”，因此就无法指导神经网络的参数调整了。

再后来，第二类改进方法就孕育而生了。它就是当前主流的方法，也就是“深度学习”常用的“逐层初始化”(layer-wise pre-training)训练机制[7]，不同于BP的“从后至前”的训练参数方法，“深度学习”采取的是一种从“从前至后”的逐层训练方法。

小结

首先，我们讲解了如何利用多层神经网络搞定“异或”问题的方法，然后我们讲解了多层前馈神经网络和损失函数的概念。

在下一讲中，我们将用图文并茂的方式，详细讲解BP算法和梯度递减的概念，特别是这个“梯度递减”概念，它还会深深影响“深度学习”算法。