深度学习入门（5）

参考原文链接🔗：https://developer.aliyun.com/article/93540

《三字经》的开篇第一句就是：“人之初，性本善”。对于神经网络来说，这句话为“网之初，感知机”。感知机是一切神经网络学习的起点，是神经网络学习的“Hello World。

感性认识“感知机”

所谓感知机，其实就是一个由两层神经元构成的网络结构，它在输入层接收外界的输入，通过激活函数（含阈值）的变换，把信号传送到输出层，因此，它也称为“阈值逻辑单元”。

感知机虽然简单，但是已经初具神经网络的必备因素。所有“有监督”的学习，在某种程度上，都是分类的学习算法。而感知机就是有监督的学习，所以，它也是一种分类算法。

下面我们列举一个区分“香蕉和西瓜”的经典案例，来看看感知机是如何工作的。为了简单起见，我们就假设西瓜和香蕉都仅有两个特征：形状和颜色，其他特征暂且不考虑，这两个特征都是基于视觉刺激得到的。

 

 

 

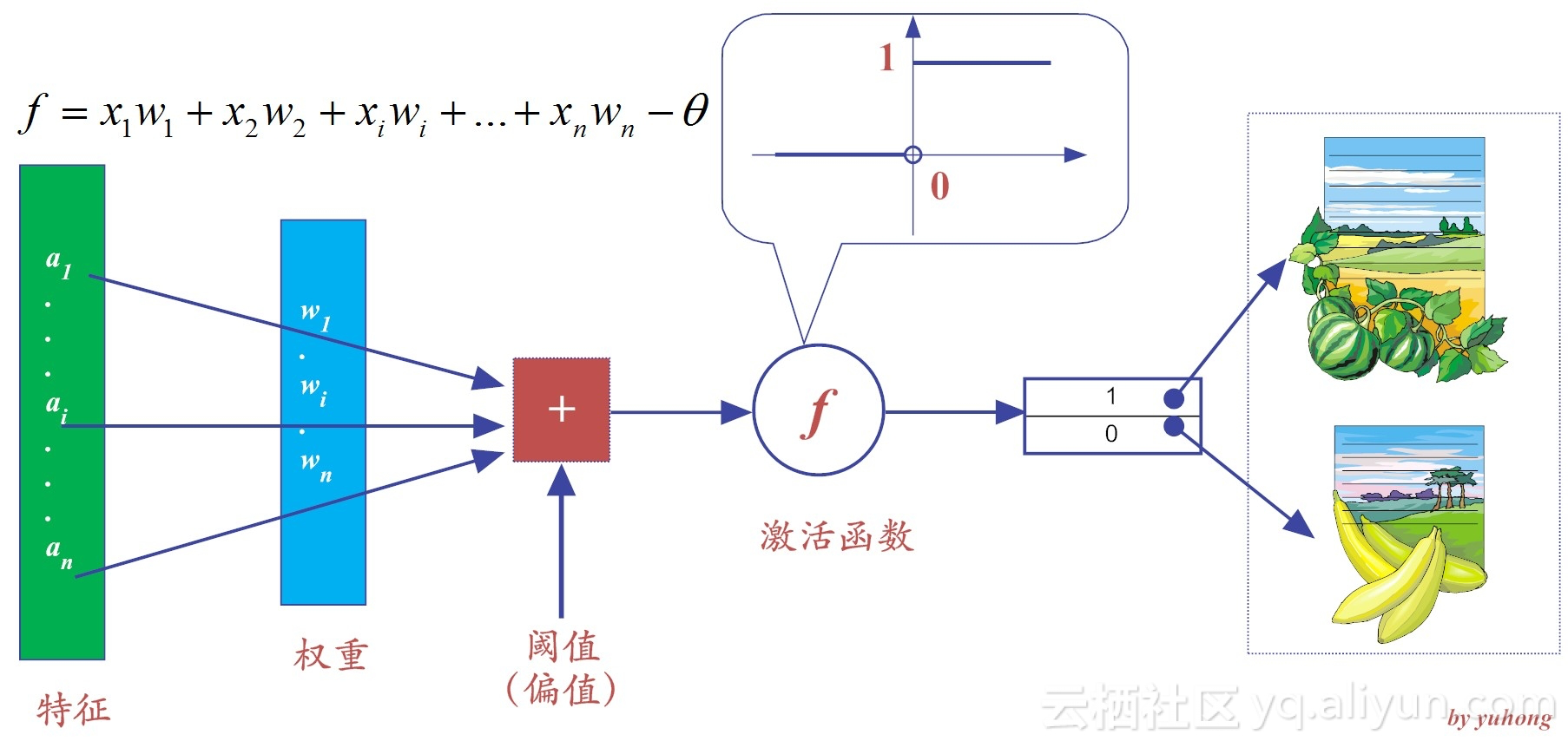
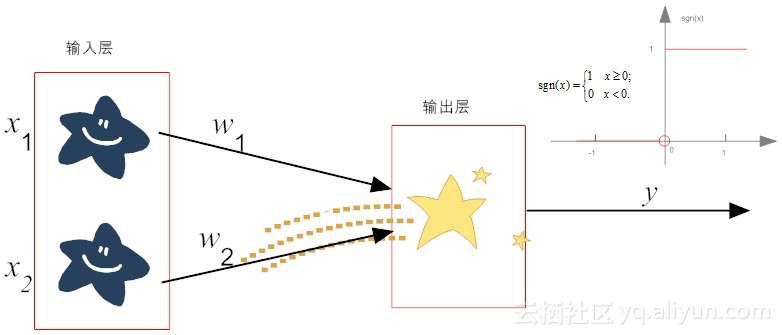
假设特征x1代表输入颜色，特征x2代表形状，权重w1和w2默认值都为1，为了进一步简化，我们把阈值θ设置为0。为了标识方便，我们将感知器输出为“1”，代表判定为“西瓜”，而输出为“0”，代表判定为“香蕉”。当然了，如果有更多类别的物品，我们就用更多的数字来标记即可。

为了方便机器计算，我们对颜色和形状这两个特征，给予不同的值，以示区别。颜色这个特征为绿色时，x1取值为1，而当颜色为黄色时，x1取值为-1；类似地，如果形状这个特征为圆形，x2取值为1，反之，形状为弯曲状时，x2取值为-1.

 

 

这样一来，可以很容易根据上图所示的公式，对于西瓜、香蕉做鉴定（即输出函数f的值），其结果分别如下图所示。

 

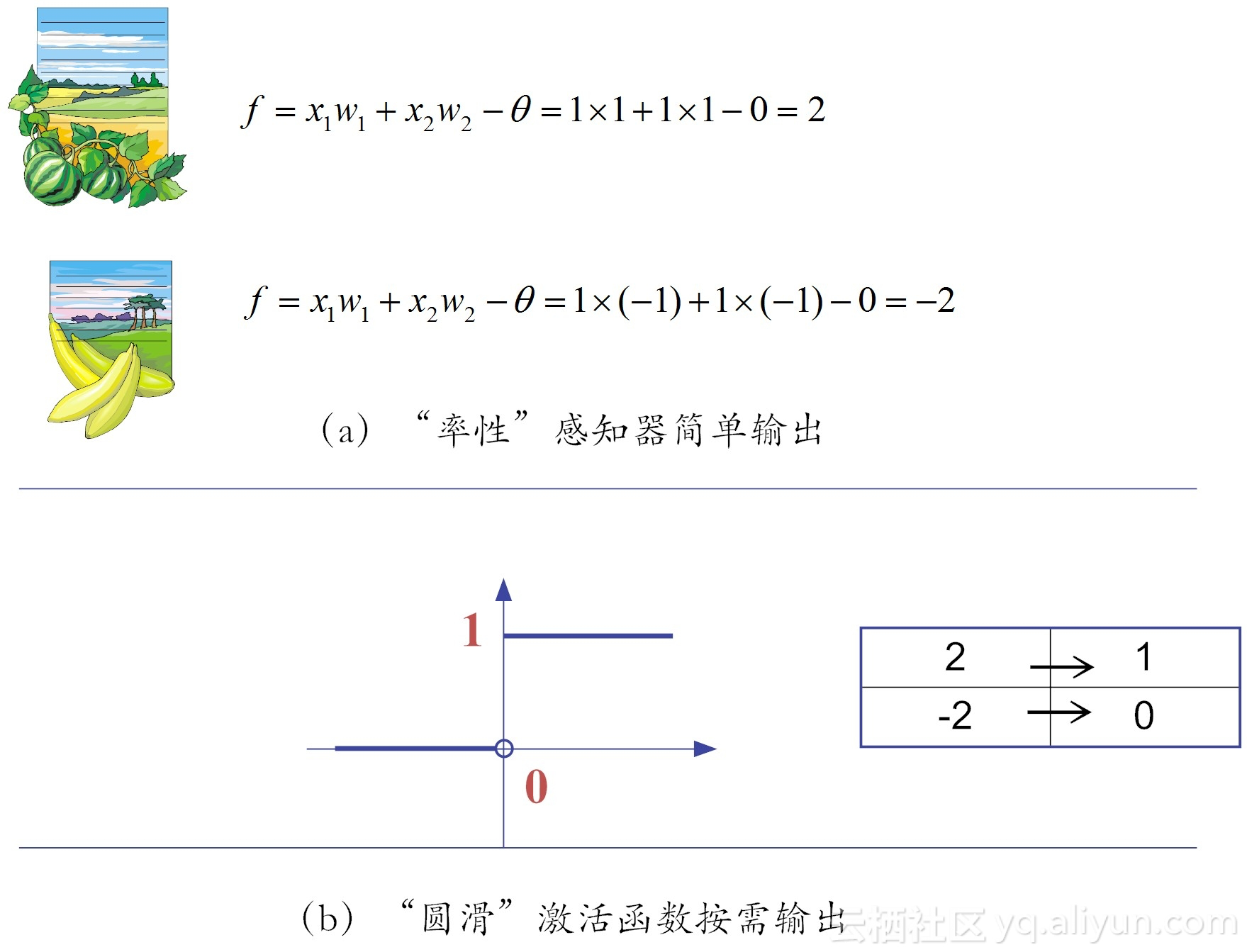
从输出可以看出，对西瓜的判定输出结果是2，而香蕉的为-2。而我们预定的规则是：函数输出为1，则判定为西瓜，输出为0，则判定为香蕉，那么如何将2或-2这样的分类结果，变换为预期的分类表达呢？这个时候就需要用到激活函数。

我们这里使用了最简单的阶跃函数。在阶跃函数中，输出规则十分简单：当x>0时，f(x)输出为1，否则输出0。通过激活函数的“润滑”之后，结果就变成了我们想要的样子，我们就搞定了香蕉和西瓜的判定。

这里需要说明的是，对象的不同特征（比如水果的颜色或形状等），只要用不同数值区分表示开来即可，具体用什么样的值，其实并无大碍。

但是，你或许会疑惑，这里的阈值和两个链接权值w1和w2，为啥这么巧分别就是0、1、1呢？如果取其他值，会有不同的判定结果吗？

事实上，我们并不能从一开始就知道这几个参数的取值，而是一点点地非常苦逼地“试错”出来的，这个过程就是感知机的学习过程。

感知机是如何学习的？

感知机学习属于“有监督学习”（即分类算法）。感知机是有明确目的导向的 ，不管是什么样的学习规则，能达到良好的分类目的，就是好学习规则。

我们知道，对象本身的特征值，一旦确定下来就不会变化，因此，所谓神经网络的学习规则就是调整权值和阈值的规则（这个结论对于深度学习而言，依然适用）。

假设我们的规则是这样的：

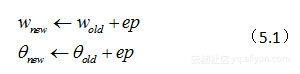
其中ep = y - y'，y为期望输出，y'是实际输出，所以，具体来说，ep是二者的差值。在后面，可以看到，这个“落差”就是整个网络中权值和阈值的调整动力。因为，很显然，如果ep为0，那么新、旧权值和阈值都是一样的，网络就稳定可用了。

下面，我们就用上面的学习规则来模拟感知机的学习过程。假设w1和w2初始值分别为1和-1，阈值为0，那么遵循下面的步骤，就可以完成判定西瓜的学习：

（1）计算判定西瓜的输出值f：

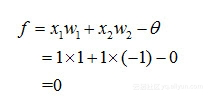
 将这个输出值带入阶跃函数中，可得y=8。

（2）显然，针对西瓜，我们期望输出的正确判定是：y=1，而现在实际输出的值y' = 0，也就是说，实际输出有误。这个时候，就需要纠偏。而纠偏，就需要利用公式所示的学习规则。于是，我们需要计算出误差ep来。

（3）计算误差ep：

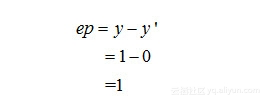
现在，我们把ep的值带入公式所示的规则中，更新网络的权值和阈值。

 

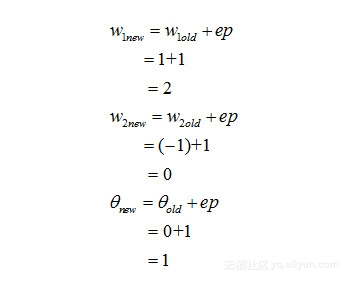
（4）那么，在新一轮的网络参数（即权值、阈值）重新学习获得后，我们再次输入西瓜的属性值，来测试一下，他能否判定正确：

 

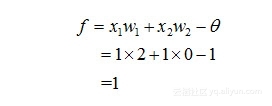
再通过激活函数（阶跃函数）处理后，输出结果y=1，判定正确。

（5）我们知道，一个对象的类别判定正确，不算好，“大家好，才是真的好！”于是，在判定西瓜正确之后，我们需要尝试在这样的网络参数下，香蕉的判定是否正确：

 

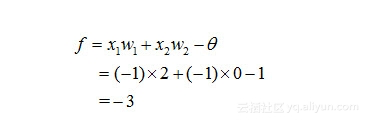
类似的，通过激活函数（阶跃函数）处理后，输出结果y=0，是正确的，误差ep为0，学习结束！

在这个案例里，仅仅通过一轮的“试错法”，我们就搞定了参数的训练，但是这只是最初级的神经网络。事实上，在有监督的学习规则中，我们需要根据输出与期望值的“落差”，经过多轮的重试，反复调整神经网络的权值，直至这个“落差”收敛到能够忍受的范围之内，训练才结束。

上面，我们只给出了感知机学习的一个感性例子，下面我们给出形式化的描述。

感知机的训练法则

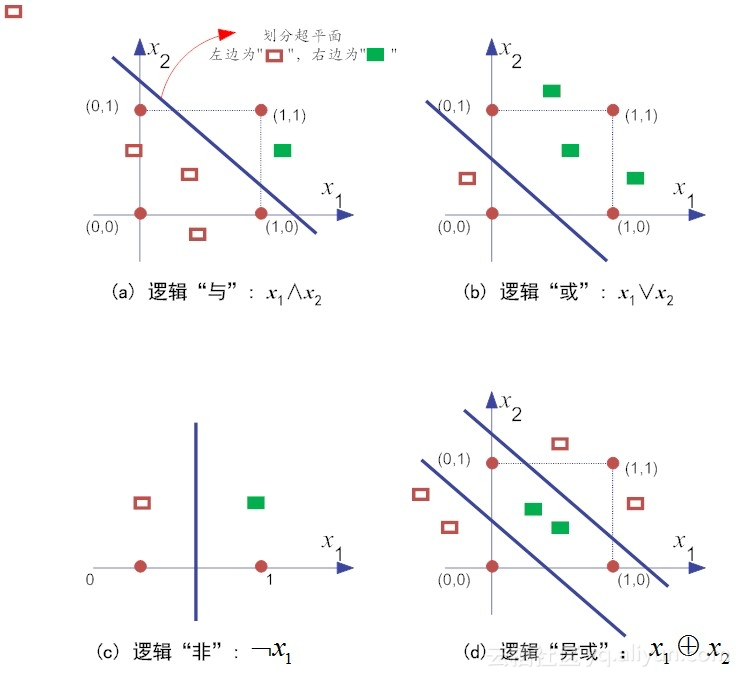
通过前边的分析，我们看出，感知机实际上是很容易实现逻辑上的“与”、“或”、“非”等原子布尔函数，如图所示，感知机实现逻辑运算，这里没有异或。

 

下面举例说明，首先，我们注意到，假设f是阶跃函数，通过合适的权值和阈值，即可完成常见的逻辑运算（既然是逻辑运算，x1和x2都只能取值0或1），例如：

（1）“与”：当权值w1=w2=1，阈值θ=2时，有：

 

 

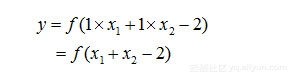
仅当x1=x2=1时，y=1，而在其他情况下（如x1和x2无论哪一个取0），y=0。

（2）类似地，“或”：当w1=w2=1，阈值θ=0.5时，有：

 此时，当x1或x2中有一个为“1”时，那么y=1，在其他情况下（x1和x2均都取“0”），y=0.这样我们就完成了运算。

（3）类似地，“非”：当w1=0.6，w2=0，阈值θ=0.5时，有：

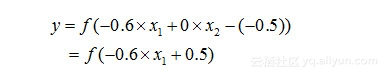
此时，当x1为“1”时，y=0，当x1为“0”时，y=1。这样，就完成了逻辑“非”的运算。

更一般的，当我们给定训练数据，神经网络中参数（权值w1和阈值θ）都可以通过不断地“纠偏”学习得到。为了方便起见，我们把阈值θ视为w0，而其权值设置为固定值“-1”，那么阈值θ就可视为一个“哑节点”。这样一来，权重和阈值的学习就可以“一统天下”成为“权重”的学习。

如此一来，感知机的学习规则就可以更加简单明了，对于训练样例（x,y）（需要注意的是，这里粗体字x表示训练集合），若当前感知机的实际输出y'，假设它不符合预期，存在“落差”，那么感知机的权值依据如公式规则调整：

其中，η∈(0,1)称为学习率，公式其实是公式的一般化描述。此公式其实是上述公式的一般化描述。由公式可知，如果（x,y）预测正确，那么可知y=y'，感知机的权值就不会发生任何变化，否则就会根据“落差”的程度做对应调整。

这里需要注意的是，学习率η的作用是“缓和”每一步权值调整强度的。它本身的大小，也是比较难以确定的。如果η太小，网络调参的次数就太多，从而收敛很慢。如果η太大，有可能会错过网络的参数的最优解。因此，合适的η的大小，在某种程度上，还依赖于人工经验。

感知机的表征能力

如果识别对象有n个特征，那么感知机可以看作，在n维实例空间（即点空间）中的超平面决策面，以向量的模式写出来就是如图所示：

 

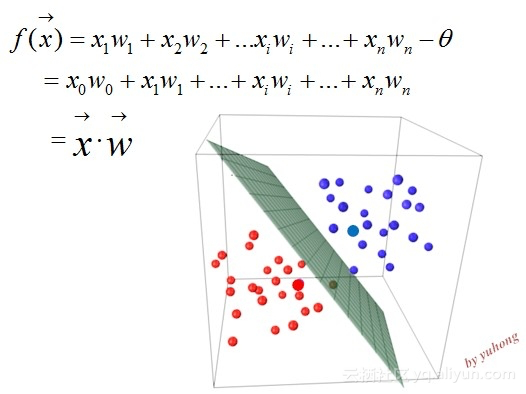
这样一来，对于超平面一侧的实例，感知机输出为1（或称判定为某一类），而对于超平面的另外一侧实例，感知机输出为0（判定为另外一类）。

由于感知机只有输出层神经元可以进行激活函数的处理，也就是说它只拥有单层的功能元神经元，因此它的学习能力是相对有限的。比如说，上边的原子布尔函数中的“与、或、非”等问题都是线性可分的问题。

前面的章节中，提到，若两类模式是线性可分的，那么一定存在一个线性超平面可以将它们区分开，也就是说，这样的感知机，其学习过程一定会稳定（收敛）下来，神经网络的权值可以学习得到。

但是对于线性不可分的原子布尔函数（如“异或”操作），就不存在简单的线性超平面将其区分开来。在这种情况下，感知机的学习过程就会发生“震荡”，权值向量就难以求得合适解。异或就是当且仅当输入值x1和x2不相等，则输出为1。反之，输出为0.

小结

在本小节，我们首先用西瓜和香蕉的判定案例，感性地谈了谈感知机的工作流程。然后，我们又给出了感知机的形式化学习规则以及感知机的表征能力。容易发现，感知机连常见的逻辑操作“异或”都难以实现。