深入学习入门(1)--感知器
写在前边:好久没有梳理自己的生活了,直到考完试才发现,很多东西以为自己会了,其实掌握的并不好,只有真正学会,转化为自己的知识才是学习真正的意义,囫囵吞枣、假装刻苦只能感动了自己结果最后还是一无是处。
参考原文链接🔗:https://www.zybuluo.com/hanbingtao/note/433855
什么是深度学习?
要想知道什么是深度学习,首先要知道,什么是学习。
学习的定义:“如果一个系统,能够通过执行某个过程,就此改善了它的性能,那么这个过程就是学习”。学习的核心目的,就是改善性能。
什么是机器学习?
对于计算机系统而言,通过运用数据及某种特定的方法(比如统计的方法或推理的方法),来提升机器系统的性能,就是机器学习。
更为具体的定义是:对于某类任务(Task,简称T)和某项性能评价准则(Performance,简称P),如果一个计算机程序在T上,以P作为性能的度量,随着很多经验(Experience,简称E)不断自我完善,那么我们称这个计算机程序在从经验E中学习了。
对于一个学习问题,我们需要明确三个特征:任务的类型,衡量任务性能提升的标准以及获取经验的来源。
学习的4个象限
人类的知识在两个维度上可以分为四类,即从可统计与否上来看,可分为:是可统计的和不可统计的。从能否推理上看,可分为可推理和不可推理的。
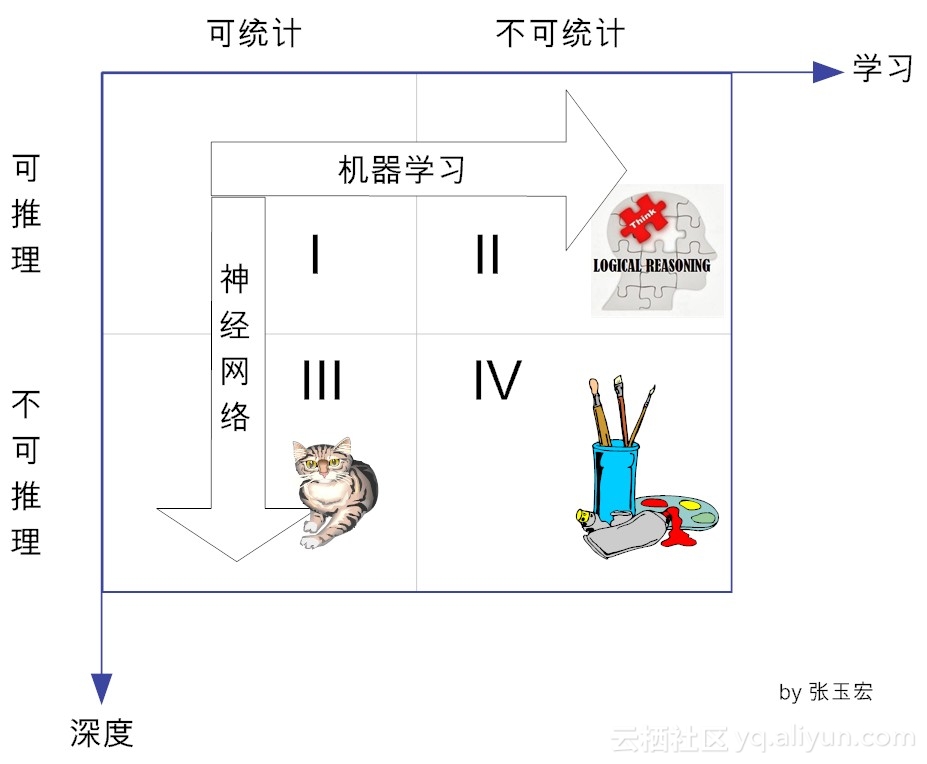
在横向方向上,对于可推理的,我们都可以通过机器学习的方法,最终可以完成这个推理。传统的机器学习方法,就是试图找到可举一反三的方法,向可推理但不可统计的象限进发。目前看来,这个象限的研究工作(即基于推理的机器学习)陷入了不温不火的境地。
在纵向上,对于可统计的、但不可推理的(即象限III),可通过神经网络这种特定的机器学习方法,以期望达到性能提升的目的。目前,基于深度学习的棋类博弈(阿尔法狗)、计算机视觉(猫狗识别)、自动驾驶等,其实都是这个象限做出了的了不起的成就。
由图可知,深度学习属于统计学习的范畴,统计机器学习的对象,其实就是数据。这是因为,对于计算机系统而言,所有的“经验”都是以数据的形式存在的。作为学习的对象,数据的类型是多样的,可以是各种数字、文字、图像、音频、视频,也可以是它们的各种组合。
统计机器学习,就是从数据出发,提取数据的特征(由谁来提取,是个大是大非的问题),抽象出数据的模型,发现数据中的知识,最后又回到数据的分析与预测当中去。
机器学习的方法论
在深度学习中,经常有“end-to-end(端到端)”学习的提法,与之相对应的传统机器学习是“Divide and Conquer(分而治之)”。
“end-to-end”说的是,输入的是原始数据(始端),然后输出的直接就是最终目标(末端),中间的过程不可知,因此也难以知。比如说,基于深度学习的图像识别系统,输入端是图片的像素数据,而输出端直接就是或猫或狗的判定。这个端到端就是:像素-->判定。
再比如说,“end-to-end”的自动驾驶系统,输入的是前置摄像头的视频信号(其实也就是像素),而输出的直接就是控制车辆行驶指令(方向盘的旋转角度)。这个端到端就是:像素-->指令。
就此,有人批评深度学习就是一个黑箱系统,性能很好,却不知道为何而好,缺乏解释性。其实这是由于深度学习所处的知识象限决定的。深度学习在本质上属于可统计不可推理的范畴。“可统计”就是说对于同类数据,它具有一定的统计规律,这是一切统计学习的基本假设。“不可推理”其实就是“剪不断、理还乱”的非线性状态。
从哲学上讲,这种非线性状态,是具备了整体性的“复杂系统”,属于复杂性科学范畴。复杂性科学认为,构成复杂系统的各个要素,自成体系,但阡陌纵横,其内部结构难以分割。对于复杂系统,一个简单系统加上另一个简单系统,其效果绝不是两个系统的简单累加效应,而可能是大于部分之和。因此,我们必须从整体上认识这样的复杂系统。于是,在认知上,就有了一个从系统或状态(end)直接整体变迁到另外一个系统或状态(end)的形态。这就是深度学习背后的方法论。
与之对应的是“Divide and Conquer”,其理念正好相反,在哲学它属于“还原主义”。在这种方法论中,有一种“追本溯源”的蕴意包含在其内,即一个系统(或理论)无论多复杂,都可以分解、分解、再分解,直到能够还原到逻辑原点。
在意象上,还原主义就是“1+1=2”,也就是说,一个复杂的系统,都可以由简单的系统简单叠加而成(可以理解为线形系统),如果各个简单系统的问题解决了,那么整体的问题也就得以解决。比如说,很多经典力学问题,不论形式多复杂,通过不断的还原和分解,最后都可以通过牛顿的三大定律得以解决。
经典机器学习(位于第II象限),在哲学上,在某种程度上,就可归属于还原主义。传统的机器学习方式,通常使用人类的先验知识,把原始数据预处理成各种特征(feature),然后对特征进行分类。
然而,这种分类的效果,高度取决于特征选取的好坏。传统的机器学习专家们,把大部分时间花在如何寻找更加合适的特征上。因此,传统的机器学习有个更合适的称呼--特征工程。
什么是深度学习?
后来机器学习的专家们发现,可以让神经网络自己学习如何抓取数据的特征,这种学习的方式,效果更佳。于是兴起了特征表示学习的风潮。这种学习方式,对数据的拟合更加灵活好用,于是人们从自寻“特征”的苦逼生活中解脱出来。
但是这种解脱也付出了代价,那就是机器自己学习出来的特征,他们存在于机器空间,完全超越了人类理解的范畴,对人而言,就是一个黑盒世界。为了让神经完了的学习性能变得更好一些,人们只能根据经验,不断的尝试性进行大量重复的网络参数调整,十分复杂。
“麻烦不会减少,只会转移”
后来,网络进一步加深,出现了多层次的“表示学习”,它把学习的性能提升到另一个高度,这种学习的层次多了,于是人们给它取了一个特别的名称---深度学习。
深度学习的学习对象同样是数据,与传统机器学习所不同的是,它需要大量的数据,也就是“大数据”。
“恋爱”中的深度学习
在很多场景下,计算机都是人类思维的一种物化方式,换句话说,计算机的思维,都能找到人类生活实践的影子。
深度学习与人们的恋爱过程也有相通之处,以恋爱为例,男女的恋爱大致可以分为三个阶段:
第一阶段初恋期,相当于深度学习的输入层。有很多因素作为输入层的参数。对不同喜好的人,他们对输出结果的期望是不同的,自然他们对这些参数的设置的权重也是不一样的。

第二阶段热恋期,对应于深度学习的隐藏层,在这个期间,恋爱双方都要经历各种历练和磨合。这种磨合中的权重取舍平衡,就相当于深度学习中的隐藏层的参数调整,他们需要不断的训练和修正。参数调整的好,输出的结果才能是想要的。
第三阶段稳定期,自然相当于深度学习的输出层,输出结果是否合适,是否达到预期,高度取决于“隐藏层”的参数“磨合”得怎么样。
在人工智能的领域,有一个方法叫机器学习,机器学习方法里有一类算法叫神经网络,如下图所示:
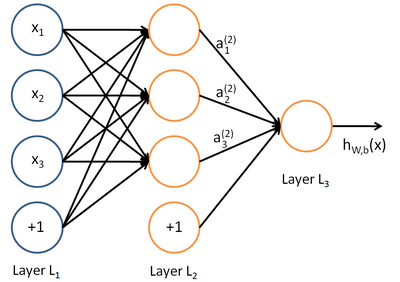
上图中每一个圆圈都是一个神经元,每条线代表神经元之间的连接。神经元被分为了很多层,层与层之间的神经元有连接,而层内之间的神经元没有连接。最左边的层叫做输入层,这层负责接收输入数据;最右边的层叫做输出层,我们可以从这层获取神经网络的输出数据,输出层和输入层之间的层叫做隐藏层。
隐藏层比较多(大于2)的神经网络叫做深度神经网络。而深度学习,就是使用深层架构(比如深度神经网络)的机器学习方法。
那么深层网络和浅层网络相比有什么优势呢?简单来说深层网络表达力更强。事实上,一个仅有一个隐藏层的神经网络就能拟合任何一个函数,但是它需要很多神经元。而深层网络用少量的神经元就能拟合同样的函数。为了拟合一个函数,要么使用一个浅而宽的网络,要么使用一个深而窄的网络,后者往往更节约资源。
深层网络也存在劣势,就是它不太容易训练,简单的说,你需要大量的数据,很多的技巧才能训练好一个深层网络。
感知器
为了理解神经网络,我们应该先理解神经网络的组成单元--神经元。神经元也叫做感知器,感知器算法是非常简单的。
感知器的定义
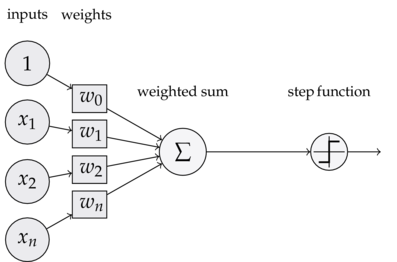
上图是一个感知器,可以看到,一个感知器有如下组成部分:
- 输入权值 一个感知器可以接受多个输入(x1,x2,...,xn | xi 属于 R),每个输入上都有一个权值wi属于R,此外还有一个偏置项b属于R,就是上图中的w0.
- 激活函数 感知器的激活函数可以有很多选择,比如我们可以选择阶跃函数作为激活函数。
- 输出 感知器的输出由下面这个公式来计算
![]()
感知器还能做什么
事实上,感知器不仅能实现简单的布尔运算,还可以拟合任何的线性函数,任何线性分类或线形回归问题都可以用感知器来解决。前面的布尔运算可以看作二分类问题,即给定一个输入,输出0(属于分类0)或1(属于分类1)。然而感知器却不能实现异或运算,异或运算不是线性的,无法用一条直线把分类0和分类1分开。
感知器的训练
前面的权重项和偏置项是如何获得的呢?这就要用到感知器训练算法:将权重项和偏置项初始化为0,然后,利用下面的感知器规则迭代的修改wi和b,直到训练完成。

每次从训练数据中取出一个样本的输入向量x,使用感知器计算其输出y再根据上面的规则来调整权重,每处理一个样本就调整一次权重。经过多轮迭代后(即全部的训练数据被反复处理多轮),就可以训练出感知器的权重,使之实现目标函数。
编程实战:实现感知器
完整代码参考Github:https://github.com/hanbt/learn_dl/blob/master/perceptron.py
接下来我们将实现一个感知器,下面是一些说明:
- 使用python语言。python在机器学习领域应用很广泛。
- 面向对象编程。面向对象是特别好的管理复杂度的工具,应对复杂问题时,用面向对象的设计方法很容易将复杂问题拆分成多个简单问题,从而解救我们的大脑。
- 没有使用numpy。numpy实现了很多基础算法,对于实现机器学习算法来说是必备的工具。但为了降低读者理解的难度,下面的代码只用到了基本的python。
下面是感知器类的实现,非常简单。
from __future__ import print_function from functools import reduce class VectorOp(object): """ 实现向量计算操作 """ @staticmethod def dot(x, y): """ 计算两个向量x和y的内积 """ # 首先把x[x1,x2,x3...]和y[y1,y2,y3,...]按元素相乘 # 变成[x1*y1, x2*y2, x3*y3] # 然后利用reduce求和 return reduce(lambda a, b: a + b, VectorOp.element_multiply(x, y), 0.0) @staticmethod def element_multiply(x, y): """ 将两个向量x和y按元素相乘 """ # 首先把x[x1,x2,x3...]和y[y1,y2,y3,...]打包在一起 # 变成[(x1,y1),(x2,y2),(x3,y3),...] # 然后利用map函数计算[x1*y1, x2*y2, x3*y3] return list(map(lambda x_y: x_y[0] * x_y[1], zip(x, y))) @staticmethod def element_add(x, y): """ 将两个向量x和y按元素相加 """ # 首先把x[x1,x2,x3...]和y[y1,y2,y3,...]打包在一起 # 变成[(x1,y1),(x2,y2),(x3,y3),...] # 然后利用map函数计算[x1+y1, x2+y2, x3+y3] return list(map(lambda x_y: x_y[0] + x_y[1], zip(x, y))) @staticmethod def scala_multiply(v, s): """ 将向量v中的每个元素和标量s相乘 """ return map(lambda e: e * s, v) class Perceptron(object): def __init__(self, input_num, activator): """ 初始化感知器,设置输入参数的个数,以及激活函数。 激活函数的类型为double -> double """ self.activator = activator # 权重向量初始化为0 self.weights = [0.0] * input_num # 偏置项初始化为0 self.bias = 0.0 def __str__(self): """ 打印学习到的权重、偏置项 """ return 'weights\t:%s\nbias\t:%f\n' % (self.weights, self.bias) def predict(self, input_vec): """ 输入向量,输出感知器的计算结果 """ # 计算向量input_vec[x1,x2,x3...]和weights[w1,w2,w3,...]的内积 # 然后加上bias return self.activator( VectorOp.dot(input_vec, self.weights) + self.bias) def train(self, input_vecs, labels, iteration, rate): """ 输入训练数据:一组向量、与每个向量对应的label;以及训练轮数、学习率 """ for i in range(iteration): self._one_iteration(input_vecs, labels, rate) def _one_iteration(self, input_vecs, labels, rate): """ 一次迭代,把所有的训练数据过一遍 """ # 把输入和输出打包在一起,成为样本的列表[(input_vec, label), ...] # 而每个训练样本是(input_vec, label) samples = zip(input_vecs, labels) # 对每个样本,按照感知器规则更新权重 for (input_vec, label) in samples: # 计算感知器在当前权重下的输出 output = self.predict(input_vec) # 更新权重 self._update_weights(input_vec, output, label, rate) def _update_weights(self, input_vec, output, label, rate): """ 按照感知器规则更新权重 """ # 首先计算本次更新的delta # 然后把input_vec[x1,x2,x3,...]向量中的每个值乘上delta,得到每个权重更新 # 最后再把权重更新按元素加到原先的weights[w1,w2,w3,...]上 delta = label - output self.weights = VectorOp.element_add( self.weights, VectorOp.scala_multiply(input_vec, rate * delta)) # 更新bias self.bias += rate * delta def f(x): """ 定义激活函数f """ return 1 if x > 0 else 0 def get_training_dataset(): """ 基于and真值表构建训练数据 """ # 构建训练数据 # 输入向量列表 input_vecs = [[1, 1], [0, 0], [1, 0], [0, 1]] # 期望的输出列表,注意要与输入一一对应 # [1,1] -> 1, [0,0] -> 0, [1,0] -> 0, [0,1] -> 0 labels = [1, 0, 0, 0] return input_vecs, labels def train_and_perceptron(): """ 使用and真值表训练感知器 """ # 创建感知器,输入参数个数为2(因为and是二元函数),激活函数为f p = Perceptron(2, f) # 训练,迭代10轮, 学习速率为0.1 input_vecs, labels = get_training_dataset() p.train(input_vecs, labels, 10, 0.1) # 返回训练好的感知器 return p if __name__ == '__main__': # 训练and感知器 and_perception = train_and_perceptron() # 打印训练获得的权重 print(and_perception) # 测试 print('1 and 1 = %d' % and_perception.predict([1, 1])) print('0 and 0 = %d' % and_perception.predict([0, 0])) print('1 and 0 = %d' % and_perception.predict([1, 0])) print('0 and 1 = %d' % and_perception.predict([0, 1]))
运行结果如下图,以上感知器已经完全实现了and函数,还可以利用感知器实现其他的函数。

小结
在本小节,我们了解了“机器学习”的核心要素,那就是通过对数据运用,依据统计或推理的方法,让计算机系统的性能得到提升。而深度学习,则是把由人工选取对象特征,变更为通过神经网络自己选去特征,为了提升学习的性能,神经网络的表示学习的层次比较多。以上仅仅给出机器学习和深度学习的概念性描述,在下一小节中,我们将给出机器学习的形式化表示,传统机器学习和深度学习的不同之处在哪里,以及什么是神经网络等。我们还将讨论另外一种感知器:线性单元,并由此引出一种可能是最最最重要的优化算法:梯度下降算法。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号